《沒有王者之路》讀後感
讓我們重拾學習幾何數學的樂趣吧!
在求學階段,相信「數學」這個學科應該是許多人的夢魘,但對我來說,一直到高中接觸到微積分之前,倒是自己特別喜歡以及擅長的學科。尤其是曾經遇到的每一位數學老師大多帶有 ”數學是宇宙之間唯一不變的真理”,甚至 ”數學是神” 的傳教熱忱,我也就篤信至今。
可惜的是步入社會之後,數學往往只會偶然出現在房屋分期貸款、基金報酬率、BMI 值的計算之中 (說實話,我也只會直接套用 excel 函數或網路上的現成試算軟體啦!),你不會再記得雞兔同籠、植樹問題,更不會記得二元一次聯立方程式或三角函數,然而,當你讀到《沒有王者之路》這本書,提到歐基里德的《原本》裡頭如何證明三角形內角合是 180 度,以及純粹只用幾何方式來證明「畢氏定理」,那些在學生時代曾經順利解題之後的成就感或虛榮已經不停地在心裡頭重新湧現。
http://www.books.com.tw/products/0010492923
沒有王者之路《幾何原本》
作者: 歐基里得/原作;翁秉仁/著
繪者:Akibo
出版社:網路與書出版
出版日期:2011/01/07
語言:繁體中文
《原本》成書於西元前三百年左右,距離今天兩千三百年,《原本》的作者是亞歷山卓的歐基里得(Euclid of Alexandria),他的生卒年根據推測大概是公元前330~260年,正是馬其頓英主亞歷山大開始發展勢力,開創希臘化文化的初期。《原本》是一本數學著作,章節安排有著嚴謹的結構,全書由定義、公設、設準、命題(定理)、證明,以及符號和圖像所構成,全書共十三卷。
《原本》其實是歐基里得將古希臘數學集大成的著作,包括了希臘科學數學家:泰利斯、畢達哥拉斯、希波克拉提斯等人的成果。導讀者翁秉仁教授認為《原本》之所以是經典,是因為歐基里得採用了非常特殊的編纂法,就是推理的方法或邏輯。歐基里得的原創性不是表現四百多個命題的敘述,因為許多命題在當時是已知的知識。歐基里得的天才表現在他有精準深刻的眼光,選擇恰當的公設,又有驚人的推理能力,可以一步步將這許多命題整合成一個體系。引用笛卡兒的譬喻,歐基里得不是只找出一條鐵鍊,而是將許多條推理的長練,編織成一張鐵鍊網,將所有的《原本》命題都固定在五個牢靠的首環上──亦即五個公設上,包括著名的「平行公設」。
歐基里得運用希臘文明的資源,將過去零散的經驗知識,整理成不容置疑的真理。他展示的這種發展人類知識的新方法,日後稱為「公設演繹法」,讓人類得以在這個變化、偶然、不可知的世界上,平地一聲雷,突然有了一個典範,可以協助人類分析、判定並取得確定的真理,這在人類的思想史上,是一個了不起的天才成就。
關於歐基里德的《原本》,史上第一個中文譯本是在明朝末年 (1607年) 由徐光啟與義大利傳教士利瑪竇合譯的《幾何原本》。在卷首的〈幾何原本雜義〉有一段話相當有意思:
此書有四不必:不必疑,不必揣,不必試,不必改。有四不可得:欲脫之不可得,欲駁之不可得,欲減之不可得,欲前後更置之不可得。
書裡頭也引用了愛因斯坦的一段話來證明能夠「證明」定理這件事是如何讓人感到不可思議的奇妙:
十二歲剛開學時,我經歷了人生…奇妙的事,一本處理歐氏幾何的小書,上頭提到三角形的三高交於一點,這件事絕非顯然,但是書上卻以不容置疑的確定性,證明了這個命題。那種清澈與確定的感覺,讓我留下難以形容的印象。
再舉個例,我拿到這本神聖幾何小書前,舅舅曾經告訴我畢氏定理,經過一番奮鬥後,我用相似三角形的方法「證明」了這個定理,任何人第一次經歷這種事,都會覺得人類竟然能夠達到這樣的確定性與純粹思考,實在是不可思議。
在這裡,我也摘要書中一段命題讓大家複習一下國中的幾何證明:
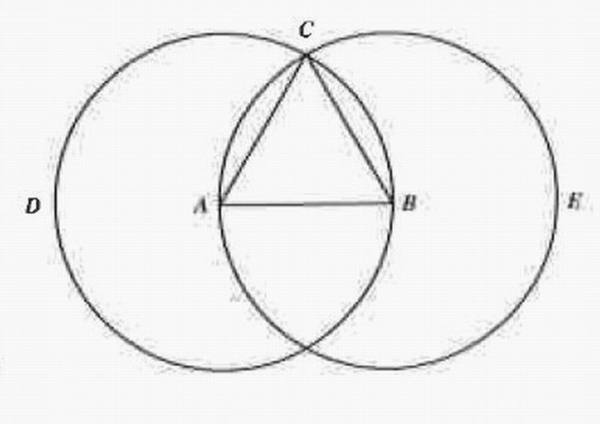
命題l
在一個已知有限直線上作一個等邊三角形。
設AB是已知有限直線。
那麼,要求在線段AB上作一個等邊三角形
以A為心,且以AB為距離畫圓BCD;
再以B為心,且以BA為距離畫圓ACE;
由兩圓的交點C到點A,B連線CA,CB。
因為點A是圓CDB的圓心,AC等於AB。
又點B是圓CAE的圓心,BC等於BA。
但是已經證明了CA等於AB;
所以線段CA,CB都等於AB。
而且等於同量的量彼此相等。
所以CA也等於CB。
三條線段CA,AB,BA彼此相等。
所以三角形ABC是等邊的,即在已知有限直線AB上
作出了這可個三角形。
這就是所要求作的。
而從古到今,好像都會提到一個問題:有什麼方法可以更快學會數學?
遠在公元前 200 多年以前,埃及的統治者托勒密一世也是向歐基里德問說:「有沒有比《原本》更快學習幾何的方法?」
歐基里德當下直言:「幾何學裡沒有王者之路。」
我想這句話相當值得每一位學生及家長深思。
|


 字體:小 中 大
字體:小 中 大









