字體:小 中 大
字體:小 中 大 |
|
|
|
| 2021/07/20 12:15:16瀏覽2973|回應3|推薦81 | |
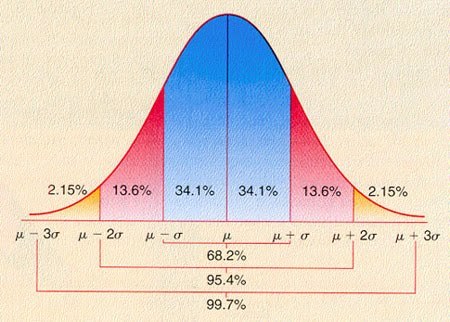
很久很久以前,還在念大學的時候,看了一本薄薄的小書,書名叫作「統計的魔術」。 書中所述,並不是一位穿著黑色衣裝,在有著黑色背景的舞台上,拿著「統計」這種道具,幻化出一齣齣巧奪神工魔術戲碼的魔術師。而是說只要運用「統計數字」就能巧妙的傳達主事者想要表達的意境。這些「統計數字」是百分之百真實的,卻能告訴讀者一些完全不同、近乎虛幻的解答。 就以最常見且普遍被理解的「平均數」和「中位數」來說好了。 幾年前有一個例子,官員表示國人平均薪資四萬八千元。嚴格來說,這個數字並沒有錯,錯就錯在這個數字沒有加入中位數和整體所得分配型態說明。怎麼說呢?先來看看平均數和中位數代表的意義好了。 此處以簡單易懂、使用最多的「算術平均數」為例。算術平均數的定義就是將母體中全部數值相加,求出總和,再除以這個母體中總個體數得出的平均值。從這個定義不難想像,如果群體中有極端值,不管是最高值或最低值,都會對平均數造成扭曲。 「中位數」,顧名思義,就是將一組資料從小到大排序後,最中間的數。但一般為了便於說明,對於數量龐大的資料都會加以分組,所以中位數也就是位置居中的那一組數字。它代表的意思是將所觀測到的資料分成相等個數的兩部分,一半個體數的值比中位數小、另一半個體數的值比中位數大。 好了,了解了這兩個常見的統計數字,咱們仍用官員說的國人平均薪資來看看數字是怎麼變魔數吧!在變魔術之前,先看看兩張分配圖,一是典型的常態分配圖,二是民國105年可支配所得與人數折線圖。 常態分配是最均勻的分布,分配圖型是一個鐘型,也就是說在這種分配之下,平均數和中位數都位在鐘型中間最高點上。但一般數列不可能如此均勻,真實的分配圖型比較可能是左偏或右偏的非常態分配。
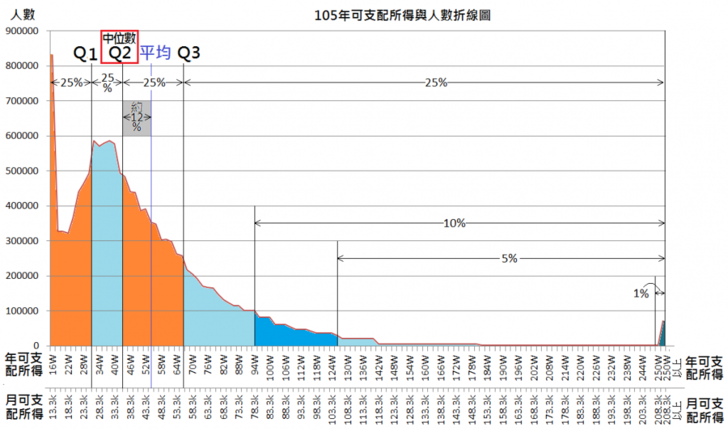
再來看看「105年可支配所得與人數折線圖」。從圖型分布很容易發現明顯左偏,左偏是因為所得為13.3k的極端值人數太多,又有大約63%的人民所得低於平均數43.3k,加上受到只有少數5%的國民所得超過100k(其中超過200k的人數更大約只有8萬人左右)的牽引,使得平均數拉高。這時候如果說我國平均月所得為43.3k,看起來好看,但卻不能表達真實情形。
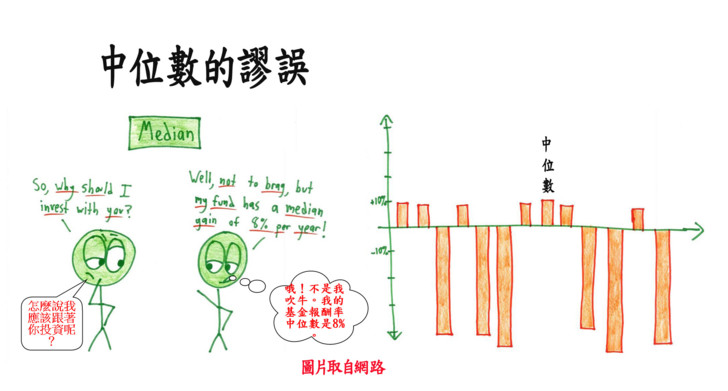
接著我們把中位數加進來說明,當年我國所得中位數是33.3k(比平均數少了10k),表示有一半的人口所得低於此,有四分之一的人口所得低於25k、有近150萬的人口數所得低於20k呢! 看來,中位數比較能反映真相,平均數則魔術般的美化了結論。 卻也未必。來看看網路上的兩副漫畫吧!原來不追究真相的結果,中位數也和平均數一樣會騙人呢!
有趣吧! 再來看看最近沸沸揚揚的覆蓋率吧! 已注射第一疫苗覆蓋率[i]: = 已注射第一疫苗人數 / 台灣人口總數 = 4,242,075 / 23,487,509 = 18.06 % 疫苗劑次人口比: = (已注射第一疫苗人數 + 已注射第二劑人數[ii])/台灣人口總數 = (4,242,075 + 95,197) / 23,487,509 = 18.47 % 現有疫苗覆蓋率: = 現有疫苗數 / 台灣人口總數 = 8,897,200 / 23,487,509 = 37.88 % 好了,這三個比例比較接近平均數的概念。如果您是魔術師,你會選那一個呢? 難怪馬克吐溫要引述英國前首相Disraeli的話:「謊言有三種,謊言、該死的謊言,以及統計數字」。 如果沒能了解數字背後的真實意義,就算「真實」的「統計數字」也能讓人掉入虛幻的美麗陷阱。 |
|
| ( 心情隨筆|心情日記 ) |