字體:小 中 大
字體:小 中 大 |
|
|
|
| 2020/10/10 09:47:09瀏覽1043|回應0|推薦8 | |
Python機器學習筆記(十四):卷積類神經網路(Convolutions Neural Networks, CNN)基礎觀念整理 先前粗略涉獵的多層次感知器類神經網路,最大問題在於它會忽略資料的形狀。例如,輸入影像的資料時,通常包含每個像素的水平位置、垂直位置、顏色等三維資訊,但多層次感知器類神經網路的輸入處理必須是平面的、也就是須變成一維的資料,這將去除影像的形狀資訊,因而失去一些重要的空間資料,像不同影像但類似的空間可能有著相似的像素值,而不同顏色之間也可能具有某些關連性、而遠近不同的像素彼此也具有不同的關聯性,而這些資訊只有在三維形狀中才能保留下來。 其次,多層次感知器類神經網路,是就整張輸入圖像進行學習比對,相較之下,CNN則是藉由在相似的位置上比對大略特徵,反能取得較佳的圖像比對識別效能。
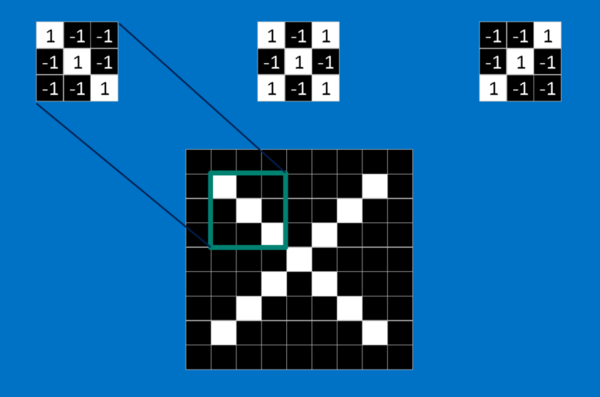
從一個非常簡單的例子來說明CNN:辨識圖片上的符號是圈圈還是叉叉。我們借由第一張圖,來了解CNN是如何運作的。圖片中最左邊的小圖,是我們要輸入識別的圖像,而最右邊則是CNN對輸入影像判定其為圈圈或叉叉的投票表決結果。而夾在輸入與結果之間的各個方塊,則是構成CNN的各個步驟流程。 卷積(convolution) 在CNN步驟流程最左邊的「卷積」方塊,是CNN運作的第一個步驟。 「卷積」的原理,是透過一個指定尺寸的window(如3*3大小),由上而下依序滑動取得圖像中「特徵圖」(feature map)進行比對。一張圖片裡的每個特徵都像一張更小的圖片,也就是更小的二維矩陣。這些特徵會捕捉圖片中的共通要素。以叉叉的圖片為例,它最重要的特徵包括對角線和中間的交叉。也就是說,任何叉叉的線條或中心點應該都會符合這些特徵。
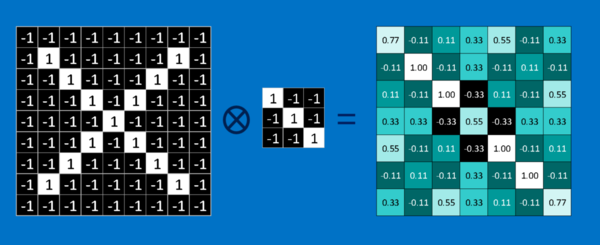
以第二張圖為例說明「卷積」的概念。輸入的圖片影像從電腦角度,只是一群的二維矩陣、帶有位置編號的像素,如白色格子的值為 1,黑色格子的值為 -1。要計算特徵和圖片局部的相符程度,只要將兩者各個像素上的值相乘、再將總和除以像素的數量。如果兩個像素都是白色(值為 1),乘積就是 1 * 1 = 1;如果都是黑色(值為 -1),乘積也是 (-1) * (-1) = 1。也就是說像素相符的乘積為 1,像素相異的乘積為 -1。如果兩張圖的每個相素都相符,將這些乘積加總、再除以像素數量就會得到 1;反之,如果兩者的像素完全相異,就會得到 -1。重複上述過程、歸納出圖片中各種可能的特徵,即可以根據每次計算得出的值和位置,製作一個新的二維矩陣,這也就是利用特徵篩選過後的原圖,如第三張圖。它可以告訴我們在原圖的哪些地方可以找到該特徵。值越接近 1 的局部和該特徵越相符,值越接近 -1 則相差越大,至於值接近 0 的局部,則幾乎沒有任何相似度可言。
下一步則是將同樣的方法應用在不同特徵上,得出圖片中各個部位的卷積圖。最後我們會得到一組篩選過的原圖,每一張圖都對應了一個特徵,如第四張圖。我們可以將整段卷積運算,簡單想成單一的處理步驟。在 CNN的運作裡,這個步驟被稱為卷積層,這也代表後面可有更多層。
線性整流單元(Rectified Linear Unit,ReLU) 接在「卷積」之後的步驟是「線性整流單元」,它的數學原理是將之前按「卷積」步驟得出的所有負數轉為 0,這個技巧可以避免 CNN 的運算結果趨近 0 或無限大。 池化(pooling) 「池化」功能很單純,就是將輸入的圖片尺寸縮小,以減少每張「特徵圖」的維度,但還是保留了每個範圍和各個特徵的相符程度。 「池化」用來縮小圖像尺寸的作法主要有三種:最大化(Max-Pooling)、平均化(Mean-Pooling)、隨機(Stochastic-Pooling)。「池化」後的資訊更專注於圖片中是否存在相符的特徵,而非圖片中哪裡存在這些特徵。這能幫助 CNN 判斷圖片中是否包含某項特徵,而不必分心於特徵的位置,其好處有: •加快系統運作的效率 •具有抗干擾的作用:圖像中某些像素在鄰近區域有微小偏移或差異時,對「池化」的輸出影響不大,結果仍是不變的 •減少過度擬合(over-fitting)的情況 以上的流程可想成單一的處理步驟,這也代表後面可有更多層。 全連接層(Full connected layer) 「全連接層」本質上可視為多層次感知器類神經網路中的輸入層、隱藏層、輸出層。在之前的「池化」層,沒有任何可供學習的參數,但在「全連接層」中,每層都有如感知器中的個自「加權參數」與「偏誤單元」,可透過梯度下降法等反向傳播(backpropagation)技巧來學習調整。 所以當 CNN 判斷一張新的圖片時,這張圖片會先經過許多低階層,再抵達全連結層。在投票表決之後,擁有最高票數的選項將成為這張圖片的類別。 圖片及內容參考來源:
|
|
| ( 知識學習|其他 ) |