Python機器學習筆記（十）：模型學習效能評分指標（兼論新冠肺炎(COVID-19)全面普篩問題）

評斷一個模型學習效能好壞與否 ，簡單地說，直接看其對未看過數據的「分類標籤」的「預測準確度」即可，但如何對「預測準確度」評分，讓我們先來認識所謂的「混淆矩陣」（confusion matrix)。

一、混淆矩陣

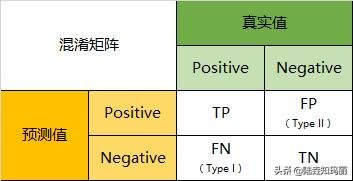
圖一即是混淆矩陣的圖形化說明。假設數據集只有二個「分類標籤」，「陽性」（positive, P）及「陰性」（negative, N），圖一的橫軸代表真實的「類別標籤」，縱軸則是模型對「類別標籤」的預測結果。依照「類別標籤」的真實情況與模型預測結果的對應情形，我們可將混淆矩陣劃分為四個區塊。左上角是「類別標籤」的真實情況為陽性，模型也正確預測為陽性，此時我們將其稱為「真陽性」（True positive, TP）。左下角則是模型將真實的陽性「類別標籤」，誤判為陰性，此情形則被稱為「偽陰性」（False negative, FN）。右上角部份，「類別標籤」的真實情況為「陰性」，模型卻預測為「陽性」，我們稱此為「偽陽性」（False positive, FP），右下角區塊，則是模型正確預測「類別標籤」為陰性，此情形稱之為「真陰性」（True negative, TN）。

二、「真陽率」（true positive rate, TPR）與「偽陽率」（false positive rate, FPR）

瀏覽完混淆矩陣的TP、FN、FP與TN四個區塊後，我們就可接著來看TPR與FPR這二個專有名詞。上文中一直出現的「陽性」二字，可視為在預測（或檢測）過程中我們所關注的重點，譬如現今熱門的新冠肺炎檢測話題，相信大家都已耳熟能詳了，「陽性」是指檢測結果為感染新冠病毒，「陰性」就表示沒事。在檢測結果為「陽性」情形下，所謂的「真陽率」TPR，是指真正感染新冠肺炎的比例有多高。而「偽陽率」FPR，則是指並沒得病，卻發假警報的機率。

從混淆矩陣，TPR及FPR可分別定義如下：

1.TPR = TP/P = TP/(TP+FN)

2.FPR = FP/N = FP/(TN+FP)

三、模型效能評分指標

我們接下來看幾個常用的模型效能評分指標

1.預測正確率（accuracy, ACC）

ACC的觀念很簡單，全部的資料裏（P+N），「陽性」（P）資料正確判定（TP）及「陰性」資料沒有誤判（TN）的二者合計比率，即

ACC = （TP+TN）/（P+N）=  （TP+TN）/（TP+FN+TN+FP）

2.精準度（precision, PRE）

PRE的意義是指，被模型判定為「陽性」的資料中，「真陽性」（TP）的比重有多高，即

PRE = TP/（TP+FP）

3.召回率（recall, REC）

REC即是「真陽率」TPR，意指一個「陽性」資料，有多高機率能被正確判定。

REC = TPR = TP/P = TP/（TP+FN）

4.F1分數

F1分數是「精準度」與「召回率」的組合判斷

F1 = 2 * （PRE*REC）/（PRE+REC）

四、大人冤枉啊！

假設我們有個罪犯偵測模型，一個犯罪者，有99%的機率會被模型偵測出來（真陽率99%），但清白的人，則會有1%機率被模型誤判（偽陽率1%）。整體而言，這時模型的預測正確率ACC為99%，我們就能依此說模型有很高的效能嗎？！

我們舉一個例子。在一個有101個人的場合，有個人的錢包被偷了，對其他100個人來說，有1個人是小偷（P），其他99人則是清白的（N）。由於真正小偷只有一人，在「真陽率」TPR為99%情形下，模型的「真陽性」TP=P*TPR=1*0.99=0.99。另一方面，因有99人是清白的，在「偽陽性」FPR為1%時，模型的「偽陽性」FP=N*FPR=99*0.01=0.99。這時模型從這100人中抓出一人說他是小偷，模型預測結果的「精準度」PRE有多高？

PRE=TP/（TP+FP）=0.99/（0.99+0.99）=0.5

一個「預測正確率」達99%的模型，所偵測出的嫌疑犯，其被冤枉的機率竟高達50%？！

造成上述看似矛盾的結果，是小偷人數遠低於清白人士（P<<N）所造成的，解決之道是合理地降低清白人士的人數。假設在上個例子中，經調查在100人中，僅有10個人曾接觸過被害人，所以真正的小偷就在這10個人裏面，1人為小偷（P），9人為清白（N）。在模型僅對這10個人偵測情形下，此時的

TP=P*TPR=1*0.99=0.99

FP=N*FPR=9*0.01=0.09

PRE=TP/（TP+FP）=0.99/（0.99+0.09）=0.9167

這時模型偵測出的嫌疑犯，其被冤枉的機率就可大幅降低到一成以內（1-0.9167=0.0833）。

五、新冠肺炎普篩問題

從上面小偷例子可知，在新冠肺炎在社區傳染擴散開來之前，實施普篩的效益不大，因此時社區中未感染者遠多於被感染者（P<<N），只要篩檢結果有「偽陽率」FPR存在，因人數較多的未感染者所造成過高的「偽陽性」FP檢測結果，不僅易造成社會人心恐慌，更會造成醫療資源錯置，反影響到真正需要使用到醫療資源的人。

所以不進行亂槍打鳥式的普篩，僅先對高危險群體進行篩檢，降低「偽陽性」假警報數量的干擾，是方向大致正確的篩檢策略。