字體:小 中 大
字體:小 中 大 |
|
|
|
| 2022/07/19 13:29:21瀏覽2744|回應0|推薦0 | |
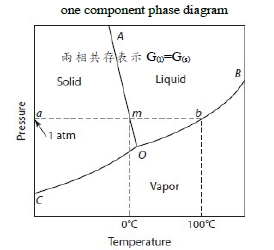
Ch. 10 binary phase diagram(先複習材導相圖) 相圖與∆Gᴹ(Xᵢ) curve的關係
Binary phase diagram(A+B), P=1 atm
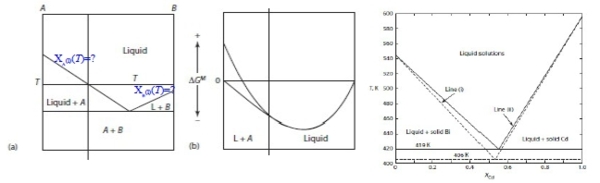
熱力學去找Xᴃ₍ₗ₎(T)=? , Xᴃ₍ₛ₎(T)=?決定liquidus/solidus lines. Gibbs free energy curves, ∆Gᴹ(Xᴃ) ∆Gᴹ=Xᴀ∆Gᴀ+Xᴃ∆Gᴃ, ∆Gᵢ=RTlnaᵢ ⸫∆Gᴹ=XᴀRTlnaᴀ+XᴃRTlnaᴃ i.e. aᵢ=γᵢXᵢ → ∆Gᴹ=∆Gᴹ,id+∆Gxs, ∆Gᴹ,id=XᴀRTlnXᴀ+XᴃRTlnXᴃ, ∆Gxs=XᴀRTlnγᴀ+XᴃRTlnγᴃ=ΩXᴀXᴃ=RTαXᴀXᴃ
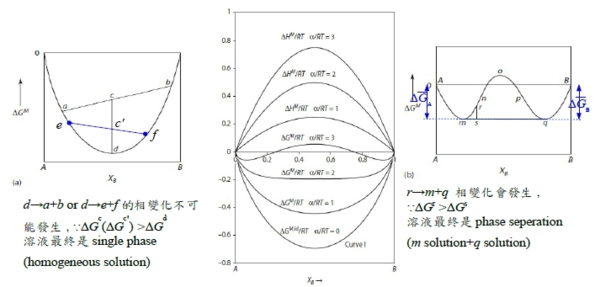
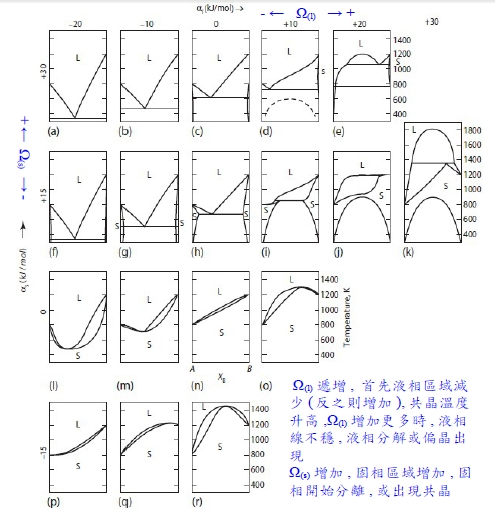
§regular solution: ∆Gᴹ(Xᴃ) curve? 先天條件: 1. ∆Sᵢ=∆Sᵢid =-RlnXᵢ, 2. ∆Hᵢ=f(Xᵢ) only! Indep. of T. ∆Hᵢxs=∆Hᵢ=RTlnγᵢ (1)γᵢ<1, span="" style="font-family:times new roman , serif" data-mce-style="font-family: times new roman , serif;">⸫Ω<0 and α<0 2="" span="">γᵢ>1, ⸫Ω>0 and α>0 → ∆Gᴹ/RT=∆Gᴹ,id/RT+αXᴀXᴃ, 當α>0且持續增加時, ∆Gᴹ/RT曲線即從向上凹變成中間凸向上的曲線
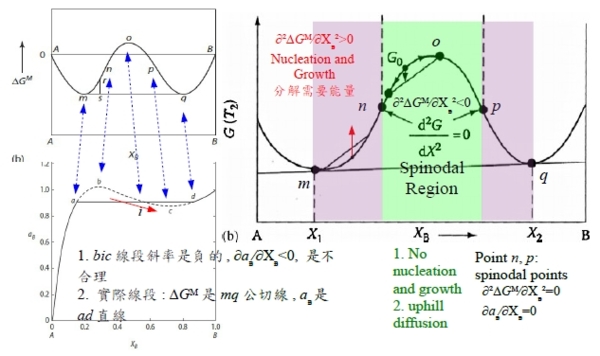
∆Gᴹ=∆Gᴹ,id+ΩXᴀXᴃ, Ω>0: m, q公切線, (solution m+solution q)共存 ∆Gᴀᵐ=∆Gᴀq →RTlnaᴀᵐ=RTlnaᴀq ⸫aᴀᵐ=aᴀq ; ∆Gᴃᵐ=∆Gᴃq →RTlnaᴃᵐ=RTlnaᴃq ⸫aᴃᵐ=aᴃq mnopq曲線只是數學,沒有物理意義;實際上的∆Gᴹ曲線是Am+mq公切線+qB的連線, Am是α₁ phase, mq是α₁+α₂共存, qB是α₂ phase. §phase stability in regular solution ⸪RTα=Ω(Ω>0 and α>0), when T fixed, α<αᶜᵣ(when T=Tᶜᵣ) single homo. Phase; or α>αᶜᵣ phase seperation. 所以當溫度下降, α變大時, ∆Gᴹ曲線可用regular solution模擬, α solution simulation by regular solution
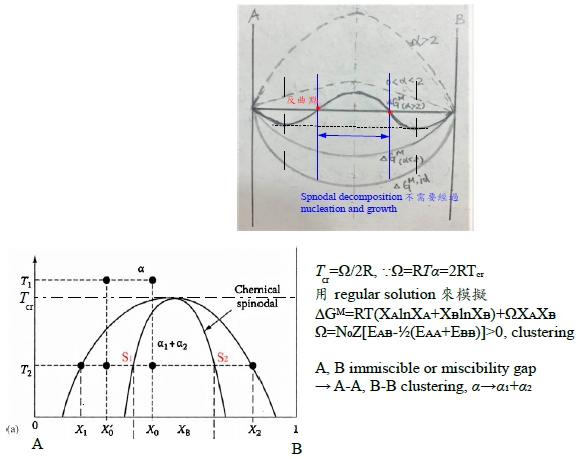
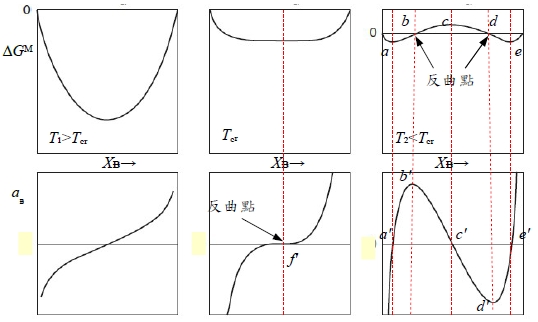
α=αᶜᵣ, ∆Gᴹ=XᴀRTlnXᴀ+XᴃRTlnXᴃ+ΩXᴀXᴃ=RT[XᴀlnXᴀ+(1-Xᴀ)ln(1-Xᴀ)]+ΩXᴀ(1-Xᴀ), ∂∆Gᴹ∕∂Xᴀ=0 → RT[lnXᴀ+1-ln(1-Xᴀ)-1]+Ω(1-2Xᴀ)=0, ∂²∆Gᴹ∕∂Xᴀ²=0 → RT[1/Xᴀ+1/(1-Xᴀ)]-2Ω=0, ⸫RT[1/Xᴀ+1/(1-Xᴀ)]= 2Ω=2RTα → α=αᶜᵣ=2 ∂³∆Gᴹ∕∂Xᴀ³=0 → RT[-1/Xᴀ²+1/(1-Xᴀ)²]=0 ⸫1/Xᴀ²-1/Xᴃ²=0 → Xᴀ=Xᴃ=0.5 ⸪Ω=RTα, ⸫Ω=RTᶜᵣ∙2 → Tᶜᵣ=Ω/2R given Ω(fixed): T>Tᶜᵣ → α<2 homogeneous="" solution="" span="">T<Tᶜᵣ → α>2 phase seperation.
∆Gᴹ=RT(XᴀlnXᴀ+XᴃlnXᴃ)+RTαXᴀXᴃ=(1)+(2), (1)=RT(XᴀlnXᴀ+XᴃlnXᴃ), (2)=RTαXᴀXᴃ ⸪(1)與溫度無關, (2)與溫度呈負相關: T↑ 造成(1)↓(<0); font="">T↓ 造成(1)↑(<0) span="" style="font-family:times new roman , serif" data-mce-style="font-family: times new roman , serif;">⸫T<Tᶜᵣ→ phase seperation.
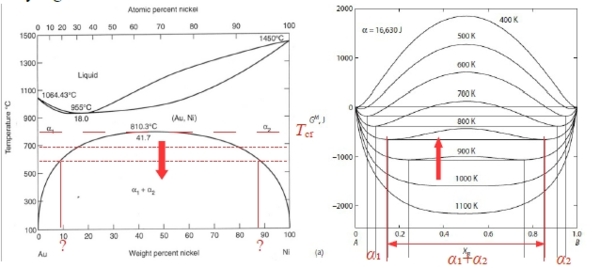
Spinodal point at Tᶜᵣ的數學特色: ∂∆Gᴹ∕∂Xᴀ=0, ∂²∆Gᴹ∕∂Xᴀ²=0, ∂³∆Gᴹ∕∂Xᴀ³=0 →αᶜᵣ=2 , Rtα=Ω ⸫Tᶜᵣ=Ω/2R. Fig. 10.6 Ω=16630J/mole, Tᶜᵣ=1000K
aᴃ(Xᴃ) curve, f point反曲點, at Tᶜᵣ 其特性: ∂aᴃ∕∂Xᴃ=0, and ∂²aᴃ∕∂Xᴃ²=0 pf: given ∆Gᴹ eq., ∆Gᴃ=RTlnaᴃ=∆Gᴹ+(1-Xᴃ)(∂∆Gᴹ∕∂Xᴃ) →對Xᴃ做微分 ∂∆Gᴃ∕∂Xᴃ=RT/aᴃ(∂aᴃ∕∂Xᴃ)=(∂∆Gᴹ∕∂Xᴃ)-(∂∆Gᴹ∕∂Xᴃ)+(1-Xᴃ)(∂²∆Gᴹ∕∂Xᴃ²)=(1-Xᴃ)(∂²∆Gᴹ∕∂Xᴃ²) ⸫RT/aᴃ(∂aᴃ∕∂Xᴃ)=(1-Xᴃ)(∂²∆Gᴹ∕∂Xᴃ²)=0, ⸪∂²∆Gᴹ∕∂Xᴃ²=0 → ∂aᴃ∕∂Xᴃ=0 ∂∆Gᴃ∕∂Xᴃ→對Xᴃ做微分 ∂²∆Gᴃ∕∂Xᴃ²=-RT/aᴃ²(∂aᴃ∕∂Xᴃ)²+RT/aᴃ(∂²aᴃ∕∂Xᴃ² )=-(∂²∆Gᴹ∕∂Xᴃ²)+(1-Xᴃ)(∂³∆Gᴹ∕∂Xᴃ³) ⸪∂aᴃ∕∂Xᴃ=0, ∂²∆Gᴹ∕∂Xᴃ²=0, ∂³∆Gᴹ∕∂Xᴃ³=0 → ∂²aᴃ∕∂Xᴃ²=0 when Tᶜᵣ, b, d是∆Gᴹ curve上的反曲點, 在aᴃ(Xᴃ) curve上為極值b和d, 其特性: ∂aᴃ∕∂Xᴃ=0, ∂²∆Gᴹ∕∂Xᴃ²=0
§10-5 isomorphous phase diagram
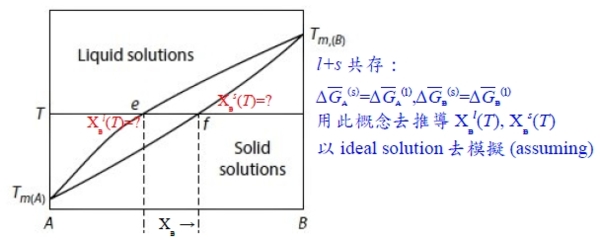
l+s兩相共存的自由能放在一起討論,需要有一參考狀態來比較: ∆G₍ₛ₎ᴹ=RT(XᴀlnXᴀ+XᴃlnXᴃ), ∆G₍ₗ₎ᴹ=RT(XᴀlnXᴀ+XᴃlnXᴃ) standard state: 為方便起見,在該溫度T之下,純元素i的平衡狀態定為standard state, Gᵢ⁰=0 ⸪Tₘ,ᴀ<T<Tₘ,ᴃ ⸫pure A的平衡狀態定為A₍ₗ₎ → Gᴀ₍ₗ₎⁰=0, Gᴀ₍ₛ₎⁰>0 pure B的平衡狀態定為B₍ₛ₎ → Gᴃ₍ₛ₎⁰=0, Gᴃ₍ₗ₎⁰>0 consider s → l melting, ∆Gₘ₍ᴀ₎= Gᴀ₍ₗ₎⁰- Gᴀ₍ₛ₎⁰ given: Tₘ,ᴀ, ∆Hₘ⁰₍ᴀ₎, cₚᴀ₍ₛ₎, cₚᴀ₍ₗ₎ ⸪Tₘ,ᴀ<T ∆Gₘ₍ᴀ₎(T)=∆Hₘ₍ᴀ₎(T)-T∆Sₘ₍ᴀ₎(T)=? ∆Hₘ₍ᴀ₎(T)=∆Hₘ⁰₍ᴀ₎+∫ᴛₘᵀ∆cₚᴀdT , ∆cₚ=cₚᴀ₍ₗ₎-cₚᴀ₍ₛ₎=0(Assume) ∆Sₘ₍ᴀ₎(T)=∆Sₘ⁰₍ᴀ₎+∫ᴛₘᵀ(∆cₚᴀ/T)dT , i.e. ∆Sₘ⁰₍ᴀ₎=∆Hₘ⁰₍ᴀ₎/Tₘ,ᴀ ⸫∆Gₘ₍ᴀ₎(T)≈∆Hₘ⁰₍ᴀ₎-T(∆Hₘ⁰₍ᴀ₎/Tₘ,ᴀ)=∆Hₘ⁰₍ᴀ₎[(Tₘ,ᴀ-T)/Tₘ,ᴀ], 同理pure B: T<Tₘ,ᴃ ∆Gₘ₍ᴃ₎(T)=∆Hₘ⁰₍ᴃ₎[(Tₘ,ᴃ-T)/Tₘ,ᴃ]
參考座標: Gᴀ₍ₗ₎⁰=0, Gᴃ₍ₛ₎⁰=0 ∆G₍ₗ₎ᴹ=RT(XᴀlnXᴀ+XᴃlnXᴃ)+Xᴃ∆Gₘ₍ᴃ₎...(1), ∆G₍ₛ₎ᴹ=RT(XᴀlnXᴀ+XᴃlnXᴃ)+Xᴀ(-∆Gₘ₍ᴀ₎)...(2) l+s共存: ∆Gᴀ₍ₛ₎=∆Gᴀ₍ₗ₎...(3), ∆Gᴃ₍ₛ₎=∆Gᴃ₍ₗ₎...(4) and ∆Gᵢ=RTlnaᵢ=∆Gᴹ+(1-Xᵢ)(∂∆Gᴹ∕∂Xᵢ) ∆Gᴀ₍ₛ₎=RT(XᴀlnXᴀ+XᴃlnXᴃ)-Xᴀ∆Gₘ₍ᴀ₎+(1-Xᴀ)[RT(lnXᴀ-lnXᴃ)-∆Gₘ₍ᴀ₎]=RTlnXᴀ₍ₛ₎-∆Gₘ₍ᴀ₎ ∆Gᴀ₍ₗ₎=....=RTlnXᴀ₍ₗ₎ ⸫根據(3), RTlnXᴀ₍ₛ₎-∆Gₘ₍ᴀ₎=RTlnXᴀ₍ₗ₎ → Xᴀ₍ₗ₎/Xᴀ₍ₛ₎=exp(-∆Gₘ₍ᴀ₎/RT)...(5) ∆Gᴃ₍ₛ₎=RT(XᴀlnXᴀ+XᴃlnXᴃ)-Xᴀ∆Gₘ₍ᴀ₎+(1-Xᴃ)[RT(-lnXᴀ+lnXᴃ)+∆Gₘ₍ᴀ₎]=RTlnXᴃ₍ₛ₎ ∆Gᴃ₍ₗ₎=....=RTlnXᴃ₍ₗ₎+∆Gₘ₍ᴃ₎ ⸫根據(4), RTlnXᴃ₍ₗ₎+∆Gₘ₍ᴃ₎=RTlnXᴃ₍ₛ₎ → Xᴃ₍ₗ₎/Xᴃ₍ₛ₎=exp(-∆Gₘ₍ᴃ₎/RT)...(6) or 1-Xᴀ₍ₗ₎=(1-Xᴀ₍ₛ₎)exp(-∆Gₘ₍ᴃ₎/RT) 將(5)代入 → 1-Xᴀ₍ₛ₎∙e-∆Gₘ₍ᴀ₎/RT =(1-Xᴀ₍ₛ₎)∙e-∆Gₘ₍ᴃ₎/RT ⸫ Xᴀ₍ₛ₎=(1-e-∆Gₘ₍ᴃ₎/RT)/(e-∆Gₘ₍ᴀ₎/RT-e-∆Gₘ₍ᴃ₎/RT) and Xᴀ₍ₗ₎=e-∆Gₘ₍ᴀ₎/RT∙(1-e-∆Gₘ₍ᴃ₎/RT)/(e-∆Gₘ₍ᴀ₎/RT-e-∆Gₘ₍ᴃ₎/RT) *Positions of points of double tangency are not influenced by choice of standard states; they are determined only by T, ∆Gₘ₍ᴀ₎, ∆Gₘ₍ᴃ₎. 照常理,擴散由濃度高往低運動,反應發生也是自由能從高變低的過程,活性自然也是由大變小,同物質的活性到處相等才達到平衡! aᵢ value depends on standard state. ⸪T<Tₘ,ᴃ def: Gᴃ₍ₛ₎⁰=0, Gᴃ₍ₗ₎⁰>0 and ∆Gᴃ=RTlnaᴃ=Gᴃ-Gᴃ⁰ → Gᴃ=Gᴃ₍ₛ₎⁰+RTlnaᴃ, w.r.t.B₍ₛ₎ or Gᴃ=Gᴃ₍ₗ₎⁰+RTlnaᴃ, w.r.t.B₍ₗ₎ i.e. Gᴃ indep. of choice ⸫ Gᴃ₍ₛ₎⁰+RTlnaᴃ, w.r.t.B₍ₛ₎=Gᴃ₍ₗ₎⁰+RTlnaᴃ, w.r.t.B₍ₗ₎ → Gᴃ₍ₗ₎⁰-Gᴃ₍ₛ₎⁰=RTln[aᴃ, w.r.t.B₍ₛ₎/aᴃ, w.r.t.B₍ₗ₎]=∆Gₘ₍ᴃ₎⁰ ⸪T<Tₘ,ᴃ ⸫∆Gₘ₍ᴃ₎⁰>0 → [aᴃ, w.r.t.B₍ₛ₎/aᴃ, w.r.t.B₍ₗ₎]>1 → aᴃ₍ₛ₎>aᴃ₍ₗ₎ 比值 aᴃ₍ₛ₎/aᴃ₍ₗ₎=e∆Gₘ₍ᴃ₎⁰/RT ∆Gₘ₍ᴃ₎(T)=∆Hₘ⁰₍ᴃ₎[(Tₘ,ᴃ-T)/Tₘ,ᴃ] Assume cₚᴀ₍ₗ₎=cₚᴀ₍ₛ₎
§10-7 modified isomorphous phase diagram
參考坐標調整與T有關
共晶、偏晶用solution model理論去理解 為簡化方便,假設A, B兩個固相不互溶,所以固相自由能固定於Xᴀ=1, 液相自由能設為ideal solution; 當T<Tₘ,ᴀ時, pure A+liquid solution共存 pure A: Gᴀ₍ₛ₎⁰, Liquid: ∆Gᴀ=∫dGᴀ =∫RTdlnaᴀ ⸫∆Gᴀ=Gᴀ₍ₗ₎-Gᴀ₍ₗ₎⁰= RTlnaᴀ₍ₗ₎→Gᴀ₍ₗ₎=Gᴀ₍ₗ₎⁰+RTlnaᴀ₍ₗ₎ ⸪pure A+liquid solution共存, Gᴀ₍ₛ₎⁰=Gᴀ₍ₗ₎=Gᴀ₍ₗ₎⁰+RTlnaᴀ₍ₗ₎ → -(Gᴀ₍ₗ₎⁰-Gᴀ₍ₛ₎⁰)=-∆Gₘ,ᴀ=RTlnaᴀ₍ₗ₎ aᴀ₍ₗ₎=e-∆Gₘ,ᴀ/RT 因為Ideal solution, aᴀ₍ₗ₎=Xᴀ₍ₗ₎ ⸫Xᴀ₍ₗ₎=e-∆Gₘ,ᴀ/RT 若給Tₘ,ᴀ, ∆Hₘ,ᴀ⁰, cₚᴀ₍ₛ₎, cₚᴀ₍ₗ₎ 就可算出∆Gₘ,ᴀ(T), Xᴀ₍ₗ₎(T)即得!
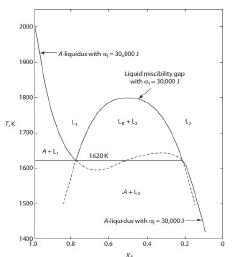
偏晶的solution model: A-liquidus line用regular solution去模擬, given: Tₘ,ᴀ=2000K, ∆Hₘ,ᴀ⁰=10KJ, Ω=30KJ -∆Gₘ,ᴀ=RTlnXᴀ₍ₗ₎+Ω(1-Xᴀ₍ₗ₎)²=-10000+5T → Xᴀ₍ₗ₎(T) ⸪∆Gₘ₍ᴀ₎(T)=∆Hₘ⁰₍ᴀ₎[(Tₘ,ᴀ-T)/Tₘ,ᴀ] liquid solution也用regular mode: ∆G₍ₗ₎ᴹ=RT(XᴀlnXᴀ+XᴃlnXᴃ)+ΩXᴀXᴃ, Ω=30KJ 液相分解溫度Tᶜᵣ=Ω/2R=1804K, 當T=T偏晶 A-liquidus solution mode: RTlnXᴀ₍ₗ₎+Ω(1-Xᴀ₍ₗ₎)²=-10000+5T liquid solution mode: ∆G₍ₗ₎ᴹ=RT(XᴀlnXᴀ+XᴃlnXᴃ)+ΩXᴀXᴃ+Xᴀ(-∆Gₘ,ᴀ) 求T偏晶=? Xᴀ(偏晶)=?
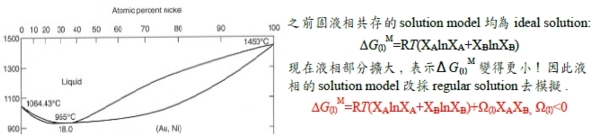
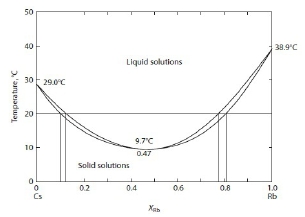
Ex. Cs-Rb phase diagram, liquidsolution: ideal, solid solution: regular and Ω₍ₛ₎=2; given: ∆Gₘ₍Cs₎=2100-6.95T, ∆Gₘ₍Rb₎=2200-7.05T
∆G₍ₗ₎ᴹ=RT(XᴀlnXᴀ+XᴃlnXᴃ), ∆G₍ₛ₎ᴹ=RT(XᴀlnXᴀ+XᴃlnXᴃ)+ΩXᴀXᴃ → 參考坐標調整 ∆G₍ₛ₎ᴹ=RT(XᴀlnXᴀ+XᴃlnXᴃ)+Xᴀ∆Gₘ₍Cs₎+Xᴃ∆Gₘ₍Rb₎, ∆G₍ₛ₎ᴹ=RT(XᴀlnXᴀ+XᴃlnXᴃ)+ΩXᴀXᴃ at Tₘᵢₙ=9.7℃, XRb=0.47 → ∆G₍ₗ₎ᴹ=∆G₍ₛ₎ᴹ→ Xᴀ(2100-6.95T)+ Xᴃ(2200-7.05T)=ΩXᴀXᴃ Ω₍ₛ₎=668J → ∆G₍ₛ₎ᴹ=RT(XᴀlnXᴀ+XᴃlnXᴃ)+668XᴀXᴃ 檢驗: 求20℃的Xᴀ, Xᴃ ? Solution model 結果得0.1, 0.13, 0.75,0.80與實驗0.1, 0.13, 0.77, 0.80比較,結果接近! |
|
| ( 知識學習|隨堂筆記 ) |