字體:小 中 大
字體:小 中 大 |
|
|
|
| 2020/09/29 21:43:41瀏覽472|回應0|推薦0 | |
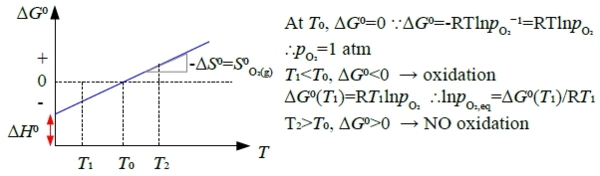
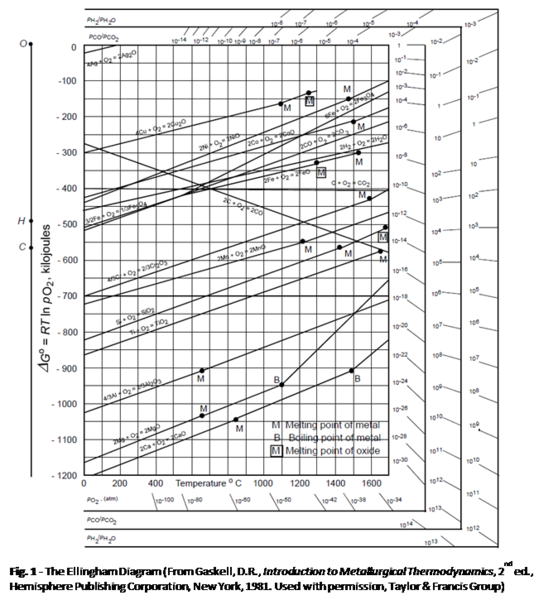
Ch. 12 氣體與凝態的反應 氧化反應: mM₍ₛ₎ + n/2O₂₍g₎ = MₘOₙ₍ₛ₎ 通式 1. ∆G⁰≡ G⁰MₘOₙ-mG⁰M-(n/2)G⁰O₂=f(T) 2. K≡pO₂⁻ₙ/₂ 3. ∆G⁰=-RTlnK=nRT/2(lnpO₂)=f(T) ∆G⁰(T)≈A+BT 近似簡化 §Ellingham diagram, fig.12-13 „stability” of metals: resistant to oxidation, 方便起見,以1mole O₂為準 M₍ₛ₎ + O₂₍g₎ = MO₂₍ₛ₎ ∆G⁰=∆H⁰-T∆S⁰ → A=∆H⁰, B=-∆S⁰=-[S⁰MO₂₍ₛ₎-S⁰M₍ₛ₎-S⁰O₂₍g₎]≈S⁰O₂₍g₎>0, 斜率>0
e.g. 2Co₍ₛ₎+O₂₍g₎=2CoO₍ₛ₎ ∆G⁰=-467800+143.7T, 2Mn₍ₛ₎+O₂₍g₎=2MnO₍ₛ₎ ∆G⁰=-769400+145.6T (i)2A₍ₛ₎+O₂₍g₎=2AO₍ₛ₎ ∆G₁⁰ (ii)B₍ₛ₎+O₂₍g₎=BO₂₍ₛ₎ ∆G₂⁰ (iii)=(ii)-(i) B₍ₛ₎+2AO₍ₛ₎=2A₍ₛ₎+BO₂₍ₛ₎ ∆G₃⁰=∆G₂⁰-∆G₁⁰ if T<Tᴇ, ∆G₃⁰<0 → A₍ₛ₎, BO₂₍ₛ₎ stable; if T>Tᴇ, ∆G₃⁰>0 → B₍ₛ₎, AO₍ₛ₎ stable stability of metals: 通常∆Gᴍ⁰<0, |∆Gᴍ⁰|越小者,抗氧化能力越好
氧壓如何加入Ellingham diagram M₍ₛ₎ + O₂₍g₎ = MO₂₍ₛ₎ ∆G⁰(T)=A+BT=-RTlnK=-RTln(pO₂)⁻¹=RTln(pO₂) ∆G⁰(T)=Rln(pO₂)∙T if pO₂ fixed, ∆G⁰~T; when pO₂=1 atm, ln(pO₂)=0; if pO₂<1 atm, ln(pO₂)<0 e.g. (i)2A₍ₛ₎+O₂₍g₎=2AO₍ₛ₎ and (ii)B₍ₛ₎+O₂₍g₎=BO₂₍ₛ₎ For metal A at T₁, pO₂=? in equilibrium 0b → (pO₂)eq=10⁻²⁰ atm ab=∆G⁰, O₂(P=1 atm) → (pO₂=10⁻²⁰ atm) ∆G⁰=∫₀ᴳ⁰dG=∫ᴘ=₁pᴼ₂RTdlnP=RTlnpO₂ at T₁, initial pO₂=1 atm → A, B oxidised. Point a → A oxidation stops. ab → AO reduction, B oxidation as pO₂ lowering down. Point b → B oxidation stops.
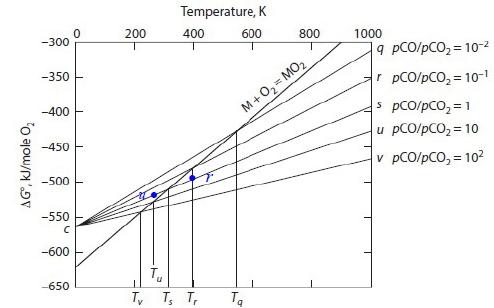
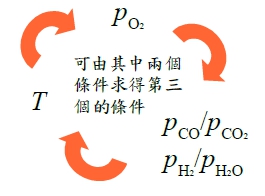
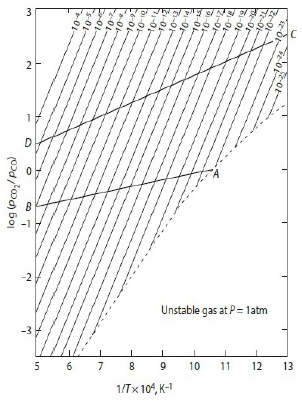
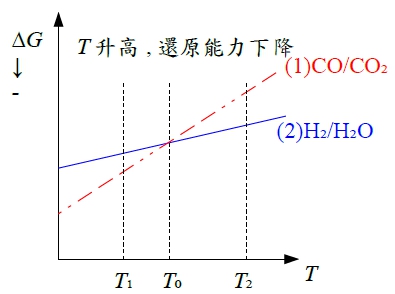
§12-6 stability of metals(or oxides) in CO/CO₂(or H₂/H₂O) mixture → maintain very low pO₂ with CO/CO₂(or H₂/H₂O) mixture 1. reducing MO₂ with CO/CO₂ mixture 2CO₍g₎ + O₂₍g₎ = 2CO₂₍g₎....(*1) ∆G₁⁰=-564800+173.62T, ∆G₁⁰=-RTlnKₚ=-RTln(pCO₂²/pCO²pO₂)=2RTln(pCO/pCO₂)+RTln(pO₂) → ln(pO₂)=-2ln(pCO/pCO₂)+∆G₁⁰/RT 已知T₀, pCO/pCO₂ 的條件, 可求得(pO₂)eq*¹ consider M₍ₛ₎ + O₂₍g₎ = MO₂₍ₛ₎....(*2) ∆G₂⁰=-RTlnK=RTln(pO₂) → ln(pO₂)=∆G₂⁰/RT → (pO₂)eq*² if (pO₂)eq*¹<(pO₂)eq*², no oxidation of M 2. nomographic scale of (pCO/pCO₂) ∆G₁⁰= 2G⁰CO₂-2G⁰CO-G⁰O₂ 在1 atm 下的標準狀態, if (pCO/pCO₂)=1/P 2CO₂₍g₎(1 atm) = 2CO₂₍g₎(P atm)....(*3) ∆G₃⁰=2RTlnP → (*4)=(*1)+(*3) 2CO₍g₎(1 atm) + O₂₍g₎(1 atm) = 2CO₂₍g₎(P atm)....(*4) ∆G₄⁰=-564800+173.62T+2RTlnP ∆G₄⁰=∆H⁰-T∆S⁰=-564800+[173.62-2Rln(1/P)]T, ∆H⁰=-564800, ∆S⁰=-[173.62-2Rln(1/P)] For fixed P or 1/P, ∆G₄⁰~T; when 1/P=1, ∆G₄⁰=∆G₁⁰; if 1/P>1, ∆G₄⁰的斜率變小; 1/P<1, ∆G₄⁰的斜率變大 3. using CO/CO₂ to reduce MO₂ M₍ₛ₎ + O₂₍g₎ = MO₂₍ₛ₎....(*5) ∆G₅⁰=RTln(pO₂) (*1)-(*5) 2CO₍g₎(1 atm) + MO₂₍ₛ₎ = 2CO₂₍g₎(1 atm) + M₍ₛ₎....(*ix) ∆Gᵢₓ⁰=-2RTln(pCO₂/pCO)=2RTln(pCO/pCO₂) 1. at Tₛ, pCO/pCO₂=1 → ∆Gᵢₓ⁰=0 2. fixed pCO/pCO₂, Tᵣ>Tₛ → no oxidation of M 3. fixed pCO/pCO₂, Tᵤ<Tₛ → M oxidised
H₂/H₂O mixture的方式和CO/CO₂ mixture一樣
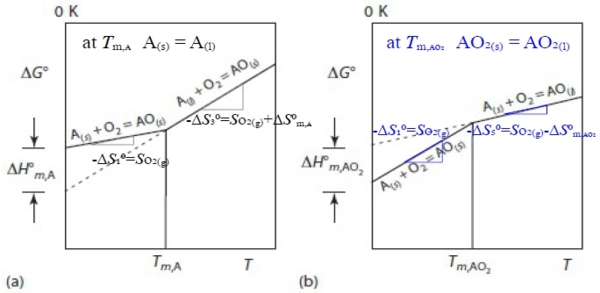
Q1: T=1000℃, pO₂=10⁻²⁶ atm → pCO/pCO₂=? pH₂/pH₂O=? Q2: e.g. Si at 800℃, pO₂ ≤? without oxidation, pCO/pCO₂≥? pH₂/pH₂O≥? §12-5 effect of temperature on Ellingham lines Ellingham line: M₍ₛ₎ + O₂₍g₎ = MO₂₍ₛ₎ ∆G⁰(T)≈A+BT=∆H⁰-T∆S⁰ e.g. A₍ₛ₎+O₂₍g₎=AO₂₍ₛ₎...(1), at Tₘ,ᴀ A₍ₛ₎ = A₍ₗ₎...(2) → (1)-(2) A₍ₗ₎+O₂₍g₎=AO₂₍ₛ₎...(3) ∆H₃⁰=∆H⁰ᴀᴏ₂₍ₛ₎-∆H⁰ᴏ₂₍g₎-∆H⁰ᴀ₍ₗ₎=∆H⁰ᴀᴏ₂₍ₛ₎-∆H⁰ᴏ₂₍g₎-∆H⁰ᴀ₍ₛ₎+∆H⁰ᴀ₍ₛ₎-∆H⁰ᴀ₍ₗ₎=∆H₁⁰-∆H⁰ₘ,ᴀ ∆S₃⁰=∆S₁⁰-∆S⁰ₘ,ᴀ=-Sᴏ₂₍g₎-∆S⁰ₘ,ᴀ=-(Sᴏ₂₍g₎+∆S⁰ₘ,ᴀ) at Tₘ,ᴀᴏ₂ AO₂₍ₛ₎ = AO₂₍ₗ₎...(4) → (1)+(4) A₍ₛ₎+O₂₍g₎=AO₂₍ₗ₎...(5) ∆H₅⁰=∆H⁰ᴀᴏ₂₍ₗ₎-∆H⁰ᴏ₂₍g₎-∆H⁰ᴀ₍ₛ₎=∆H⁰ᴀᴏ₂₍ₗ₎-∆H⁰ᴀᴏ₂₍ₛ₎+∆H⁰ᴀᴏ₂₍ₛ₎-∆H⁰ᴏ₂₍g₎-∆H⁰ᴀ₍ₛ₎=∆H⁰ₘ,ᴀᴏ₂+∆H₁⁰ ∆S₅⁰=∆S⁰ₘ,ᴀᴏ₂+∆S₁⁰=-(Sᴏ₂₍g₎-∆S⁰ₘ,ᴀᴏ₂)
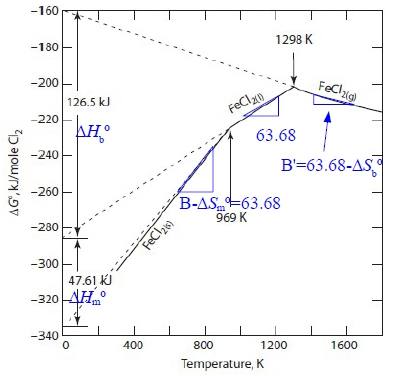
e.g. Fe₍ₛ₎ + Cl₂₍g₎ = FeCl₂₍ₛ₎...(1) ∆G₁⁰=-346300-12.68TlnT+212.9T ≈A+BT Fe₍ₛ₎ + Cl₂₍g₎ = FeCl₂₍ₗ₎...(2) ∆G₂⁰=-286400+63.68T Fe₍ₛ₎ + Cl₂₍g₎ = FeCl₂₍g₎...(3) ∆G₃⁰=-105600+41.8TlnT-375.1T≈A+BT draw Ellingham line. Given: Tₘ, FeCl₂=969K, Tᵇ, FeCl₂=1298K
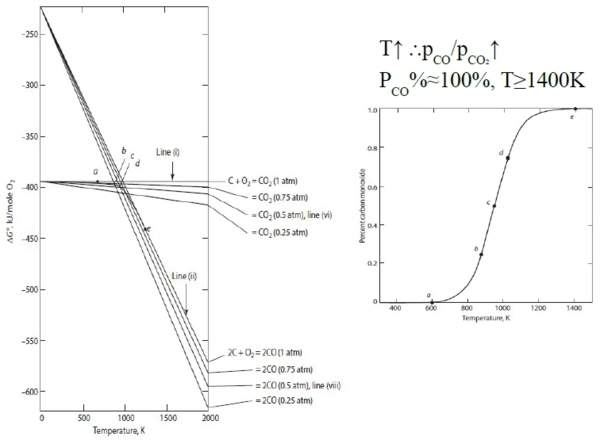
(2)-(1) FeCl₂₍ₛ₎ = FeCl₂₍ₗ₎...(4) ∆Gₘ⁰=∆G₂⁰-∆G₁⁰=59900+12.68TlnT-149.22T ∆Hₘ⁰=-T²[∂(∆Gₘ⁰/T)∕∂T]ₚ=59900-12.68T=47613, ∆Sₘ⁰=-(∂∆Gₘ⁰∕∂T)ₚ=-12.68lnT+136.54=49.35 ∆G₁⁰ ≈A+BT, A=-286400-∆Hₘ⁰=334013 J, B=63.68+∆Sₘ⁰=113.03 (3)-(2) FeCl₂₍ₗ₎ = FeCl₂₍g₎...(5) ∆Gb⁰=∆G₃⁰-∆G₂⁰=180800+41.8TlnT-438.78T ∆Hb⁰=-T²[∂(∆Gb⁰/T)∕∂T]ₚ=180800-41.8T=126543J, ∆Sb⁰=-(∂∆Gb⁰∕∂T)ₚ=-41.8lnT+396.98=97.33 ∆G₃⁰≈A+BT, A=-286400+∆Hb⁰=-159856J, B= 63.68-∆Sb⁰=-33.65 §12-6 oxides of carbon(前段) C₍ₛ₎ + O₂₍g₎ = CO₂₍g₎ ∆G₁⁰, 2C₍ₛ₎ + O₂₍g₎ = 2CO₍g₎ ∆G₂⁰ 用炭製造CO, CO₂ 2*(1)-(2) 2CO₍g₎ + O₂₍g₎ = 2CO₂₍g₎, C₍ₛ₎ + CO₂₍g₎ = 2CO₍g₎ ∆G₄⁰=-RTlnK=-RTln(pCO²/pCO₂)=f(T) 觀念: 溫度升高, (pCO/pCO₂)增加 e.g. 煉鐵的時候,高溫使還原氣CO增加,將鐵還原 怎麼控制 pCO/pCO₂ (1)C₍ₛ₎ + O₂₍g₎ = CO₂₍g₎ ∆G₁⁰=-394100-0.84T (2) 2C₍ₛ₎ + O₂₍g₎ = 2CO₍g₎ ∆G₂⁰=-223400-175.3T (3)2CO₍g₎ + O₂₍g₎ = 2CO₂₍g₎ ∆G₃⁰=-564800+173.62T (4)C₍ₛ₎ + CO₂₍g₎ = 2CO₍g₎ ∆G₄⁰=170700-174.5T ∆G₁⁰=∆G₂⁰, T₀=978K. When T> T₀, ∆G₁⁰>∆G₂⁰ → pCO變大 ⸫T↑, pCO/pCO₂↑ C₍ₛ₎ + O₂₍g₎ = CO₂₍g₎ ∆G₁⁰=GCO₂⁰-GO₂⁰- GC⁰ 1atm 1atm (5) CO₂₍g₎ = CO₂₍g₎ ∆G₅⁰=RTlnP 1atm P atm (5)+(1) C₍ₛ₎ + O₂₍g₎ = CO₂₍g₎ ∆G₆⁰=∆G₁⁰+∆G₅⁰=-394100-0.84T+RTlnP=-394100-(0.84-RlnP)T 1atm P atm (7) 2C₍ₛ₎ + O₂₍g₎ = 2CO₍g₎ ∆G₇⁰=-223400-175.3T+2RTlnP=-223400-(175.3-2RlnP)T 1 atm Patm
§12-7 upper limit of (pCO/pCO₂) at fixed T (pCO/pCO₂)增加會促使反應往左,造成碳析出 C₍ₛ₎ + CO₂₍g₎ = 2CO₍g₎ e-∆G₄⁰/RT=K₄=(pCO²/pCO₂), if P=1 atm =pCO+pCO₂ → pCO₂=1-pCO K₄=pCO²/(1-pCO)=x=e-∆G₄⁰/RT ⸫pCO=-x/2+(x²+4x)½/2, pCO₂=(2+x)/2-(x²+4x)½/2 pCO/pCO₂=[-x+(x²+4x)½]/[(2+x)-(x²+4x)½] or lower limit pCO₂/pCO=[(2+x)-(x²+4x)½]/[-x+(x²+4x)½] [∂(lnKₚ)∕∂T]ₚ=∆H⁰/RT² vant Hoff eq. → [∂ln(pCO/pCO₂)∕∂(1/T)]ₚ=∆H⁰/R
Ex-1. (1)CO₍g₎ + ½O₂₍g₎ = CO₂₍g₎ ∆G₁⁰=-282400+86.81T (2)H₂₍g₎ + ½O₂₍g₎ = H₂O₍g₎ ∆G₂⁰=-246400+54.8T (3)Co₍ₛ₎ + ½O₂₍g₎= CoO₍ₛ₎ ∆G₃⁰=-233900+71.85T which (H₂, CO) is more efficient reducing gas? ∆G₁⁰=∆G₂⁰ → T₀=1125K when T<T₀, ∆G₁⁰<∆G₂⁰, CO more efficient; if T>T₀, ∆G₁⁰>∆G₂⁰, H₂ more efficient. How mny moles of CoO can be reduced by 1 mole of H₂ at T₁ or T₂? (2)-(3) CoO₍ₛ₎ + H₂₍g₎ = Co₍ₛ₎ + H₂O₍g₎ ∆G₄⁰=-12500-17.05T T₁=873K, ∆G₄⁰=-27385, e-∆G₄⁰/RT₁=43.5=K₄= pH₂O/pH₂=x/(1-x), x=0.9775 T₂=1673K, ∆G₄⁰=-41025, e-∆G₄⁰/RT₂=19.1=K₄= pH₂O/pH₂=x/(1-x), x=0.95 How mny moles of CoO can be reduced by 1 mole of CO at T₁ or T₂? (1)-(3) CoO₍ₛ₎ + CO₍g₎ = Co₍ₛ₎ + CO₂₍g₎ ∆G₅⁰=-48500+14.96T T₁=873K, ∆G₅⁰=-35440, e-∆G₄⁰/RT₁=132=K₅= pCO₂/pCO=y/(1-y), y=0.992 T₂=1673K, ∆G₅⁰=-23472, e-∆G₄⁰/RT₂=5.41=K₅= pCO₂/pCO=y/(1-y), y=0.844
Ex-2. ZnO₍ₛ₎ + CO₍g₎ = Zn₍g₎ + CO₂₍g₎ ∆G₁⁰=177800-111.2T at T=950℃=1223K Q1: pᵢ=? if P=1 atm ∆G₁⁰=41802, e-∆G⁰/RT=0.0164=K=pZnpCO₂/pCO=pZn²/(1-2pZn), pZn=pCO₂=0.113 atm, pCO=0.774 atm ⸪pZn=pCO₂, and P=1=pZn+pCO₂+pCO, pCO=1-2pZn Q2: what is the critical pressure to condense liquid Zn from gas? Given: lnp⁰Zn₍ₗ₎=-15250/T-1.255lnT+21.79 代入T=1223K, p⁰Zn=1.49 atm 0.0164=K=pZnpCO₂/pCO=p⁰Zn²/(Pc-2p⁰Zn), Pc=138.35 atm Q3: pᵢ=? if P=150 atm ⸪P>Pc ⸫pZn=p⁰Zn=1.49 atm, 0.0164=K=p⁰ZnpCO₂/pCO...(1), P=150 atm=p⁰Zn+pCO₂+pCO...(2)聯立解 pZn=p⁰Zn=1.49 atm, pCO₂=1.61 atm, pCO=146.9 atm Q4: ZnO₍ₛ₎ + C₍ₛ₎ = Zn₍g₎ + CO₍g₎ ∆Gₓ⁰=348500-285.7T, 2ZnO₍ₛ₎ + C₍ₛ₎ = 2Zn₍g₎ + CO₂₍g₎ ∆Gₓᵢ⁰=526300-396.8T at T=1223K, ask pᵢ=? P=? Kₓ=e-∆G⁰/RT=1.094=pZn pCO, Kₓᵢ=e-∆G⁰/RT=0.0177=pZn² pCO₂, ⸪nZn=nO ⸫nZn=nCO+2nCO₂, pZn=pCO+2pCO₂ 1.094=(pCO+2pCO₂) pCO, 0.0177=(pCO+2pCO₂)² pCO₂, 聯立解一元三次式 Ex-4. 1 mole CO₂₍g₎ and 1 mole H₂₍g₎ mixed at T=1000K, P=1atm, ask pᵢ=? H₂₍g₎ + CO₂₍g₎ = H₂O₍g₎ + CO₍g₎....(1) ∆G⁰=36000-32.05T ini 1 1 0 0 f 1-x 1-x x x Kₚ=pCOpH₂O/pH₂pCO₂ ⸪ pH₂=pCO₂, pCO=pH₂O → P=1=2(pH₂+pH₂O) e-∆G⁰/RT=0.618=Kₚ=(0.5-pH₂)²/pH₂² pH₂=0.28 atm=pCO₂, pCO=0.22 atm=pH₂O Q2: CaO₍ₛ₎ 投入, (2)CaO₍ₛ₎ + 5CO₍g₎ = CaC₂₍ₛ₎ +3CO₂₍g₎ ∆G⁰(ii) = −37,480 + 300.7T, (3)CaO₍ₛ₎ + H₂O₍g₎ = Ca(OH)₂₍ₛ₎ ∆G⁰(iii) = −117,600 +145T, (4)CaO₍ₛ₎ + CO₂₍g₎ = CaCO₃₍ₛ₎ ∆G⁰(iv) = −168,400 +144T 求pᵢ=? Assume (2)(3)(4) equilibrium K₂=e-∆G⁰/RT=1.782∙10⁻¹⁴= pCO₂³/pCO⁵ if pCO=0.22 atm, pCO₂=2.09∙10⁻⁶ atm 反應不會發生 K₃=e-∆G⁰/RT=0.037=1/pH₂O pH₂O=27.027 atm 反應不會發生 K₄=e-∆G⁰/RT=18.82=1/pCO₂ pCO₂=0.053 atm (1)(4) 反應平衡, e-∆G⁰/RT=0.618=Kₚ=pCOpH₂O/pH₂pCO₂ ⸪ pCO=pH₂O , and P=1=2(pH₂+pH₂O) ⸫pH₂=0.387 atm, pCO=pH₂O= 0.113 atm, P=0.666 atm Q3: C₍ₛ₎ 投入, (5) C₍ₛ₎ + CO₂₍g₎ = 2CO₍g₎ ∆G₅⁰=170700-174.5T (1)(4)(5) all equilibrium, 1.579=e-∆G⁰/RT=K₅= pCO²/pCO₂ ⸪pCO₂=0.053 atm ⸫ p”CO=0.289 atm 0.618=Kₚ= p”COp”H₂O/p”H₂pCO₂, ⸪ p”H₂+p”H₂O=0.5, p”H₂=0.449, pH₂O=0.051 P=0.842 atm Ex-3. NiO₍ₛ₎ + Cl₂₍g₎ = NiCl₂₍g₎ + ½O₂₍g₎ at T=900K, ∆G⁰=-15490, if 90% Cl₂₍g₎ consume to produce O₂₍g₎ ask P=? NiO₍ₛ₎ + Cl₂₍g₎ = NiCl₂₍g₎ + ½O₂₍g₎ ini 1 1 0 0 f 1-x 1-x x x/2 nᴛ =1-x/2 7.905=e-∆G⁰/RT=K=pO₂½/pCl₂=[(x/2)P/(1-x/2)]½/[(1-x)P/(1-x/2)] 代入x=0.9, =0.393 atm
|
|
| ( 知識學習|隨堂筆記 ) |