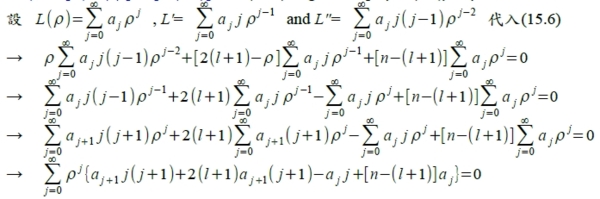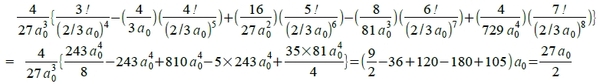原子結構與光譜 - 人生紀錄本

字體：小中大

原子結構與光譜

2023/06/29 11:42:43瀏覽969｜回應0｜推薦0

第15章原子結構與光譜

氫原子發射光譜: 1/λ=R_H{(1/n₁²)-(1/n₂²)}, n₂=n₁+1, n₁+2,... R_H=109677cm⁻¹稱為Rydberg常數,光譜包含紫外光(Lyman series)、可見光(Balmer series)和紅外線(Paschen series)...,分別n₁ =1,2,3開始;此公式表示任一光線的波數(或頻率)都是兩個項(R_H/n²)之間的差值: ṽ=T₁-T₂

氫原子的電子結構: 氫原子包含電子與原子核2個粒子,其運動方程式有原子在空間的運動及電子圍繞原子核的運動,表示成[-(ℏ²/2m‪ₑ)‪ₑ²-(ℏ²/2m_ɴ)‪_ɴ²+V(r)]ψ=Eψ, 但討論的焦點在電子結構,意即第二部分的運動,所以操作上先簡化成電子圍繞原子核的運動方程式

因此必須將整體原子的運動與電子繞核運動區分開,可以借用古典動能的概念將方程式變換成: [-(ℏ²/2m‪)‪_ᶜ_.ₘ_.²-(ℏ²/2μ)‪²+V(r)]ψ=Eψ, i.e. m=m‪ₑ+m_ɴ, μ=m‪ₑm_ɴ/m‪ₑ+m_ɴ .若把原點移至質心位置,方程式的第一項-(ℏ²/2m‪)‪_ᶜ_.ₘ_.²ψ即可忽略,簡化為[-(ℏ²/2μ)‪²+V(r)]ψ=Eψ.

→ ‪²ψ-[2μV(r)/ℏ²]ψ=-[2μE/ℏ²]ψ (15.1),

設γ=μZe²/2πε₀ℏ² i.e. V(r)=-Ze²/4πε₀r是庫侖力建立的位能, and ε=-2μE/ℏ²,代入(15.1)

→ ‪²ψ+(γ/r)ψ=εψ, ‪²以球座標微分算符取代, 1/r(∂²/∂r²)(rψ)+(1/r²)Λ²ψ+(γ/r)ψ=εψ (15.2) ,

Λ²=(1/sin²θ)(∂²/∂ϕ²)+(1/sinθ)(∂/∂θ)sinθ(∂/∂θ), 令ψ(r,θ,ϕ)=R(r)Y(θ,ϕ)代入(15.2)

1/r(∂²rR/∂r²)Y+(1/r²)RΛ²Y+(γ/r)RY=εRY 除以RY, (1/rR)(∂²rR/∂r²)+(1/r²Y)Λ²Y+(γ/r)=ε 乘以r²

→ (r/R)(∂²rR/∂r²)+(1/Y)Λ²Y+(γr)=εr² (15.3) 只有(1/Y)Λ²Y是θ,ϕ 的函數,其餘都是r的函數

設 Λ²Y/Y=-l(l+1)=常數(lZ),則(r/R)(∂²rR/∂r²)+(γr)-εr²=l(l+1) 進行整理得

∂²(rR)/∂r²+[(γ/r)-l(l+1)/r²]rR=εrR (15.4) 即為欲解的氫原子radial wave eq. 先與Schrodinger eq.對照: rR視為波函數,[(γ/r)-l(l+1)/r²]可看成電子的有效位能勢V_eff, 第一項是庫倫吸引力造成的電位能,第二項是電子繞核的角動量造成的斥力

因此設R=fe^-^r^√^ε, f比指數項更快收斂,成可接受的解,將其代入(15.4)

→ d²(rfe^-^r^√^ε)/dr²+[(γ/r)-l(l+1)/r²]rfe^-^r^√^ε=εrfe^-^r^√^ε

d²(rfe^-^r^√^ε)/dr²=d/dr(fe^-^r^√^ε+rfe^-^r^√ε-√εrfe^-^r^√^ε)=fe^-^r^√^ε-√εfe^-^r^√^ε+fe^-^r^√^ε+rf"e^-^r^√^ε-√εrfe^-^r^√^ε-√εfe^-^r^√^ε-√εrfe^-^r^√^ε+εrfe^-^r^√^ε=[rf"+(2-2√εr)f+(εr-2√ε)f]e^-^r^√^ε將展開的二次微分項代入前式

→ [rf"+(2-2√εr)f+(εr-2√ε)f]e^-^r^√^ε+[(γ/r)-l(l+1)/r²]rfe^-^r^√^ε=εrfe^-^r^√^ε

→ rf"+(2-2√εr)f+{(γ/r)-l(l+1)/r²-(2√ε/r)}rf=0 →f"+[(2/r)-2√ε]f+{(γ/r)-l(l+1)/r²-(2√ε/r)}f=0 (15.5)

變數變換r→ρ, 令r=ρ/(2√ε)

f=df/dr, f=(df/dρ)(dρ/dr)=2√εf i.e. f=df/dρ, f"=d/dr(2√εf)=4εf 代入(15.5)

4εf+[(4√ε/ρ)-2√ε]2√εf +{(2√εγ/ρ)-l(l+1)4ε/ρ²-(4ε/ρ)}f=0

→ f+[(2/ρ)-1]f +{(γ/2√ερ)-l(l+1)/ρ²-(1/ρ)}f=0, 令n=γ/(2√ε), f+[(2/ρ)-1]f +{(γ-1)/ρ-l(l+1)/ρ²}f=0

設f(ρ)=ρ^lL, f =lρ^l^-1L+ρ^lL, f=ρ^lL"+2lρ^l^-1L+l(l-1)ρ^l^-2L代入前式

→ ρ^lL"+2lρ^l^-1L+l(l-1)ρ^l^-2L+[(2/ρ)-1](lρ^l^-1L+ρ^lL)+{(γ/2√ερ)-l(l+1)/ρ²-(1/ρ)}ρ^lL=0

→ ρL"+[2(l+1)-ρ]L+[n-(l+1)]L=0 (15.6) Laguerre eq. xy"+(1-x)y+ny=0

→ a_j₊₁[j(j+1)2(l+1)(j+1)]+a_j[-j+n-(l+1)]=0, a_j₊₁=[j-n+(l+1)]a_j/[(j+1)(j+2l+2)]

當jₘₐₓ-n+(l+1)=0, L(ρ)的無窮級數多項式解就不會無限發散, a_j_ₘₐₓ₊₁後的多項式都會歸零,變成可接受的解, 所以jₘₐₓ=n-(l+1)>0, n> l+1 且l為整數,因此n,l的限制條件:

l=0,1,2,...,n-1, and l

既然n=γ/(2√ε), γ=μZe²/2πε₀ℏ²和ε=-2μE/ℏ², n=[μZe²/2πε₀ℏ²]/[2(-2μE/ℏ²)^½]

→ (-2μE/ℏ²)^½=[μZe²/4πε₀ℏ²n] → E=-μZ²e⁴/32π²ε₀²ℏ²n²=-13.6Z²/n² eV=-const./n²

同時r=ρ/(2√ε), ρ=2r[μZe²/4πε₀ℏ²n]=(r/n)[μZe²/2πε₀ℏ²]=(r/n)[mₑe²/4πε₀ℏ²](2μZ/mₑ),

令a₀=4πε₀ℏ²/mₑe² Bohr radius → ρ=(r/n)(2μZ/a₀mₑ), r=(nmₑ/2μZ)a₀ρ i.e. μ≈mₑ, r=(n/2Z)a₀ρ=na₀ρ/2Z or ρ=(2Z/na₀)r

radial wave function: R_n_,l(ρ)=ρ^l∑_j₌₀^n-^l^-1b_jρ^je^-^ρ^/2, ρ=(2Z/na₀)r and b_j₊₁=[j-n+(l+1)]b_j/[(j+1)(j+2l+2)]

ex. R₁₀(r)=ρ⁰∑_j₌₀⁰b_jρ^je^-^ρ^/2, R₁₀(r)=Ce^-Z^r^/^a^₀, 求C=? ⸪ ∫₀^∞r²R^*_n_,lR_n_,ldr=1

→ |C|²∫₀^∞r²e^-2Z^r^/^a^₀dr=1 利用部分積分2次即得 2(a₀/2Z)²|C|²∫₀^∞e^-2Z^r^/^a^₀dr=1, 2(a₀/2Z)³|C|²=1

→ |C|²=½(2Z/a₀)³, C=(1/√2)(2Z/a₀)^3/2 R₁₀(r)=2(Z/a₀)^3/2e^-Z^r^/^a^₀,

R₂₀(r)=ρ⁰∑_j₌₀¹b_jρ^je^-^ρ^/2=(b₀+b₁ρ)e^-Z^r^/2^a^₀=b₀(1-Zr/2a₀)e^-Z^r^/2^a^₀, i.e. b₁=-½b₀

→ |b₀|²∫₀^∞r²(1-Zr/2a₀)²e^-Z^r^/^a^₀dr=1, |b₀|²[∫₀^∞r²e^-Z^r^/^a^₀dr-(Z/a₀)∫₀^∞r³e^-Z^r^/^a^₀dr+(Z/2a₀)²∫₀^∞r⁴e^-Z^r^/^a^₀dr]=1

→ |b₀|²[ 2(a₀/Z)³-(Z/a₀)3!(a₀/Z)⁴+¼(Z/a₀)²4!(a₀/Z)⁵]=1, b₀=(1/√2)(Z/a₀)^3/2

R₂₀(r)=(1/√2)(Z/a₀)^3/2(1-Zr/2a₀)e^-Z^r^/2^a^₀=(1/2√2)(Z/a₀)^3/2(2-ρ)e^-^ρ^/2

R₃₀(ρ)=ρ⁰∑_j₌₀²b_jρ^je^-^ρ^/2=(b₀+b₁ρ+b₂ρ²)e^-^ρ^/2, i.e. b₁=-b₀, b₂=⅙b₀, R₃₀(ρ)=⅙b₀(6-6ρ+ρ²)e^-^ρ^/2

氫原子軌道: 波函數ψₙ_,_l_,_m_ₗ=R_n_,l(r)Y_l_,_m_ₗ(θ,ϕ), Z為原子序, radial波函數R_n_,l(r), ρ=(2Z/na₀)r

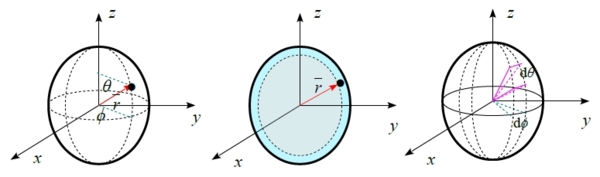
氫原子的能階:為了解薛丁格方程式,得到可接受的波函數,從邊界條件中導出3種量子數:角動量量子數l,和磁量子數mₗ是來自Y_l_,_m_ₗ(θ,ϕ),帶l的電子,其角動量大小為[l(l+1)]^½ℏ,l的值從0,1,...到n-1; mₗ值代表動量的方向,如L_z=mₗℏ, mₗ=0,±1,±2,...,±l. 第3種量子數n是主量子數,決定能量透過 Eₙ=-μe⁴/32π²ε₀²ℏ²n²=-13.6/n² eV, 所以氫原子的波函數隨n,l,mₗ而定

n-1,2,3,... l=0,1,2,...,n-1 mₗ=l,l-1,l-2,...1,0,-1,...,-l 同時在某個n值會有n²個不同(l,mₗ)的組合;也就是在Eₙ能階有n²個簡併態

Eₙ=-ℎcR_H/n², ℎcR_H=μe⁴/32π²ε₀²ℏ² L=[l(l+1)]^½ℏ, L_z=mₗℏ

ψₙ_,_l_,_m_ₗ=R_n_,l(r)Y_l_,_m_ₗ(θ,ϕ), Y_l_,_m_ₗ(θ,ϕ)=Θ_l_,|_m_ₗ_|(θ)Φ_m_ₗ(ϕ)=N_l_,_m_ₗPₗ^mₗ(cosθ)eⁱ^m^ₗϕ,

Φ_m_ₗ(ϕ)=Aeⁱ^m^ₗϕ, mₗ=0,±1,±2,...,±l

Θ_l_,|_mₗ_|(θ)=BPₗ^mₗ(cosθ) 當l為整數且|mₗ|≤l, Pₗ^mₗ(u)=(1/2^ll!)(1-u²)^|^mₗ^/2^|(d^l^+|^mₗ^|/du^l^+|^mₗ^|)(u²-1)^l, u=cosθ

R_n_,l(ρ)=ρ^l∑_j₌₀^n-^l^-1b_jρ^je^-^ρ^/2, ρ=(2Z/na₀)r and b_j₊₁=[j-n+(l+1)]b_j/[(j+1)(j+2l+2)], l=0,1,2,...,n-1, and l

機率密度: 1. 在(r,θ,ϕ)處體積元dV內發現電子的機率: ψ^*ₙ_,_l_,_m_ₗψₙ_,_l_,_m_ₗr²sinθdrdθdϕ

2. 在r到r+dr球殼內發現電子的機率: r²R^*_n_,lR_n_,ldr

3. 在角度(θ,ϕ)內發現電子的機率: Y^*_l_,_m_ₗY_l_,_m_ₗsinθdθdϕ

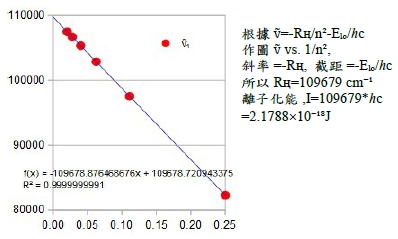
類氫原子(i.e. He⁺, Li²⁺...)指原子核外指有一個電子,其能量與l和mₗ無關,只和主量子數n相關.

被原子束縛的電子,能量較自由電子低,為負值;以氫原子為例,電子束縛態的能量

Eₙ=-ℎcR_H(1/n²), ℎcR_H=μe⁴/32π²ε₀²ℏ² 氫原子光譜可以電子能態之間的過渡來表示發射光子的能量或頻率, ℎν=ℎcR_H/n₁²-ℎcR_H/n₂² or ṽ=ν/c=R_H/n₁²-R_H/n₂² i.e. ṽ=1/λ

離子化能I: 電子吸收能量脫離原子的束縛,使原子變離子;氫原子的電子基態(n=1)E₁=-ℎcR_H, 激發成自由電子(n=∞) E_∞=0, 所以離子化能I=E_∞-E₁=ℎcR_H=2.17910⁻¹⁸J=13.6eV, 同時會發現光譜線隨n值增加而靠攏,從公式也可發現ṽ=-R_H/n²-Eₗₒ_ʷ/ℎc

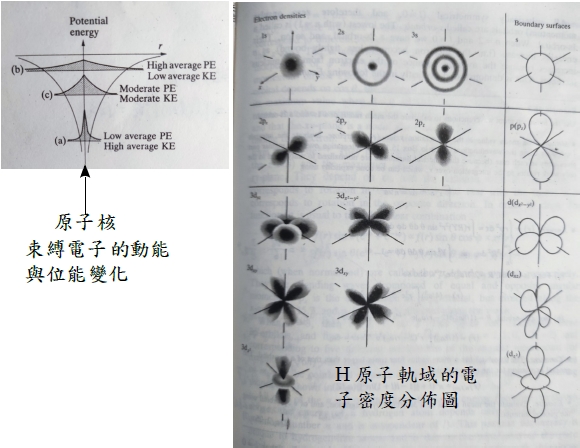
單電子原子的波函數用來描述原子結構,可稱為軌域orbital, ψₙ_,_l_,_m_ₗ=R_n_,l(r)Y_l_,_m_ₗ(θ,ϕ),徑向和角向的波函數乘積,墊子存在的機率密度:|ψₙ_,_l_,_m_ₗ|²dτ, dτ=r²sinθdθdϕdr, |ψₙ_,_l_,_m_ₗ|²代表機率覆蓋的密度,圖示中的邊界面是90%電子機率的界面以及方位節點的位置.

基態軌域: n=1, and l=mₗ=0, ψ₁₀₀=(1/πa₀³)^½e^-^r^/^a^₀與方位角無關,形狀為球形對稱,也符合位能最小的位置是電子最接近原子核的觀點,而動能變大是因波函數在原子核附近的峰值,使曲率變大所致;當電子擴散距離增加而遠離原子核,使波函數的曲率下降,造成動能減少位能上升.

同時動能增減只與徑向運動有關,因為l=0沒有角動量,因此所有s軌域因為l=0(沒有角動量),它的形狀都是球形對稱,而且ns軌域有n-1個球節面

ex. use the H atom wavefuctions to calculate the mean radius of s-orbital.

〈r〉=∫rψ²dτ=∫r(RY)²r²sinθdθdϕdr, ⸪l=0 for s-orbital, ∫Y²sinθdθdϕ=1 ⸫〈r〉=∫r³R²dr

i.e. ∫₀^∞xⁿe^-^axdx=n!/aⁿ⁺¹.

(1) 1s, R₁₀=2(1/a₀³)^½e^-^r^/^a^₀,〈r〉=∫₀^∞r³[2(1/a₀³)^½e^-^r^/^a^₀]²dr=(4/a₀³)∫₀^∞r³e^-2^r^/^a^₀dr=(4/a₀³)(3!/[2/a₀]⁴)=3a₀/2

(2) 2s, R₂₀=2(1/2a₀)^3/2(1-r/2a₀)e^-^r^/2^a^₀, 〈r〉=∫₀^∞r³[2(1/2a₀)^3/2(1-r/2a₀)e^-^r^/2^a^₀]²dr=(1/2a₀³)∫₀^∞r³[1-r/a₀+r²/4a₀²]e^-^r^/^a^₀dr=(1/2a₀³)[3!/[1/a₀]⁴-(1/a₀)(4!/[1/a₀]⁵)+(1/4a₀²)(5!/[1/a₀]⁶)]=(1/2a₀³)[6a₀⁴-24a₀⁴+30a₀⁴]=6a₀

(3) 3s, R₃₀=(2/3√3)(1/a₀)^3/2[1-2r/3a₀+2r²/27a₀²]e^-^r^/3^a^₀,

R₃₀²=(4/27a₀³)[1-4r/3a₀+16r²/27a₀²-8r³/81a₀³+4r⁴/729a₀⁴]e^-2^r^/3^a^₀

〈r〉=∫₀^∞r³[(4/27a₀³)[1-4r/3a₀+16r²/27a₀²-8r³/81a₀³+4r⁴/729a₀⁴]e^-2^r^/3^a^₀]dr=

→ r₁ₛ:r₂ₛ:r₃ₛ=3a₀/2:6a₀:27a₀/2=1:4:9

平均軌域半徑的一般式: rₙ_,_l_,_m_ₗ=n²{l+½[1-l(l+1)/n²]}(a₀/Z)

l=1的軌域(p軌域): ex. n=2, l=1 2p軌域, 角動量=√2ℏ,角動量會影響波函數的形狀,因為角動量產生的離心效應與庫倫吸引力的向心力對抗,使電子遠離原子核,對照s軌域的波函數,p軌域之波函數在原子核的振幅為零,亦即機率密度等於零.

i.e. L=Iω, I=mr² and ω=v/r, ⸫L=mvr →離心力F_ᶜ=mv²/r=L²/mr³ vs. 庫倫力Fₑ=Ze²/4πε₀r²

推論: 當l>0,波函數在原子核的振幅為零,電子存在的機率為零

l=1時,mₗ=1,0,-1有3個p軌域,對應不同的角動量mₗℏ; mₗ=0表示波函數與ϕ無關(⸪e^±i^mₗϕ=1),且數學形式為f(r)cosθ, cosθ即是在z軸上的投影,而且電子機率密度與cos²θ有關,θ=0°或180°有極大值;而θ=90°時,機率密度=0. 因此mₗ=0的p軌域稱作p_z軌域,在z軸上有最大的電子密度,並且xy平面是p_z的節面,形狀如啞鈴形

mₗ=±1時,波函數含有e^±i^ϕ項,數學形式為f(r)sinθe^±i^ϕ,當θ=0°或180°振幅為零;而θ=90°振幅最大落在xy平面,e^±i^ϕ與角動量旋轉方向有關,可利用波函數線性疊加得出p_x和p_y:

f(r)sinθ(eⁱ^ϕ+e⁻ⁱ^ϕ)f(r)sinθcosϕxf(r)...(a), f(r)sinθ(eⁱ^ϕ-e⁻ⁱ^ϕ)f(r)sinθsinϕyf(r)...(b)

(a)式中當ϕ=0°或180°, cos²ϕ=1表示最大的電子密度在x軸上;當ϕ=90°,cos²ϕ=0節線落在y軸,因此稱為p_x軌域,(b)式同理,稱為p_y軌域

d軌域: l=2, mₗ=2,1,0,-1,-2有5個d軌域,正負號相反的mₗ值的波函數,可以疊加成對形成駐波形式

徑向分佈函數: 我們知道機率密度是波函數的共軛複數相乘, |ψₙ_,_l_,_m_ₗ|²=ψ^*ψ, s軌域為球形對稱,與角向波函數Y_l_,_m_ₗ(θ,ϕ)無關,因此機率密度簡化為: ψ^*ψ(4πr²dr)=P(r)dr, 所以P(r)稱為徑向分佈函數RDF.

ex. 計算電子佔據1s軌域時, 最可能的電子半徑

ψ₁₀₀=(1/π)^½(Z/a₀)^3/2e^-Zr/^a^₀, P(r)=4πr²ψ^*ψ=4(Z/a₀)³r²e^-2Zr/^a^₀ 當P(r)=Pₘₐₓ, dP/dr=0時, r=r^*

dP/dr=4(Z/a₀)³[2r-2Zr²/a₀]e^-2Zr/^a^₀=0, r=0(不合), a₀/Z ⸫r₁ₛ=a₀=53 pm for H atom

	H	He	Li	Be	B	C	N
r^*/pm	52.9	26.5	17.6	13.2	10.6	8.82	7.56

2s軌域時,ψ₂₀₀=¼(1/2π)^½(Z/a₀)^3/2(2-Zr/a₀)e^-Zr/2^a^₀,

P(r)=4πr²ψ^*ψ=4πr²(1/32π)(Z/a₀)³(2-Zr/a₀)²e^-Zr/^a^₀=⅛(Z/a₀)³[4r²-4Zr³/a₀+Z²r⁴/a₀²]e^-Zr/^a^₀

dP/dr=⅛(Z/a₀)³{8r-12Zr²/a₀+4Z²r³/a₀²-(Z/a₀)(4r²-4Zr³/a₀+Z²r⁴/a₀²)}e^-Zr/^a^₀

= ⅛(Z/a₀)³[8-16Zr/a₀+8Z²r²/a₀²-Z³r³/a₀³]re^-Zr/^a^₀= ⅛(Z/a₀)³r(2-Zr/a₀)(4-6Zr/a₀+Z²r²/a₀²)e^-Zr/^a^₀

→ r=0, 2a₀/Z, 3±√5(a₀/Z) 最佳解: r=3+√5(a₀/Z)

( 知識學習｜科學百科 )