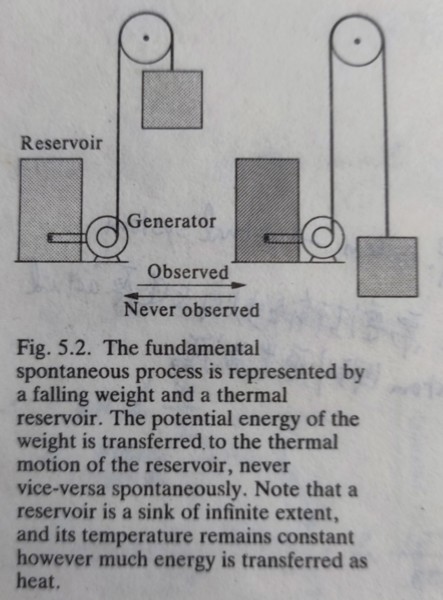
有些事自然發生,有些則不會! 譬如氣體自由膨脹、冷卻會自行發生,但壓縮氣體、做鑽石必需做功才會發生;因此自發變化spontaneous changes始終伴隨著能量〝品質〞的降低,意義上,能量被降解(degradation)成一種較分散和混亂的形式,第一定律告訴我們能量守恆,但無法判斷可行的反應是否會自己進行?若總體能量不變,變化的方向是否與能量分布的形式有關?

自發變化就是宇宙universe自然趨向較大混亂的結果

自發變化的路徑: 尋找變化方向導致總能的混亂散佈;而反向的過程往往非自然,因為混亂散佈的能量絕不可能使自己恢復成局部均勻的方式.自發變化是不可逆的過程,使能量降解同時增加熵,下面的例子也說明此特性,功轉換成熱,但熱卻無法完全轉回功!

熵:測量能量分散度

第一定律使用內能辨別可允許的變化;第二定律要用熵辨別可允許的變化中是否為自發?

了解熵的方式: 一者計算能量散佈的程度,由統計原子(分子)能階著手;另一途徑是由反應變化中的熱與散佈有關下手,兩者殊途同歸.

ex. 自由落體做功轉換成熱q^†傳入熱儲(定溫T^†)

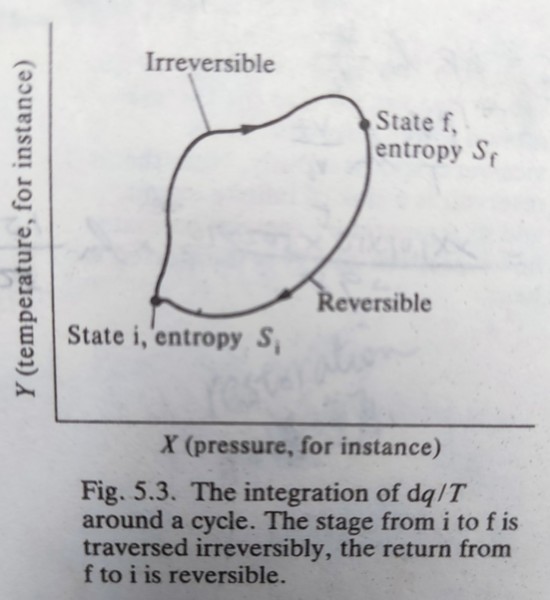
實際系統的熵變量dS^ₛʸ^ₛ可以熱儲做為參考系統來量測,假設其過程是可逆的,總熵 ∮ dS=0

→ (-dS^ₛʸ^ₛ)+(dq^†ᵣₑᵥ/T^†)=0 or dS^ₛʸ^ₛ=dq^†ᵣₑᵥ/T^†, 當實際系統與參考系統的溫度相同, dS^ₛʸ^ₛ=dq^†ᵣₑᵥ/T(⸪T=T^†),另外dq^†ᵣₑᵥ是參考系統由實際系統得到的熱,因此實際系統失去的熱dq^ₛʸ^ₛ=-dq^†ᵣₑᵥ

最後實際系統的熵變量dS^ₛʸ^ₛ=dq^ₛʸ^ₛ/T, ∆S^ₛʸ^ₛ=S_f-S_i=∫ᵢ^ᶠdq^ₛʸ^ₛ/T

ex. a perfect gas change its state from (V_i,T) to (V_f,T), w=∫ᵢ^ᶠpdV=∫ᵢ^ᶠnRTdV/V=nRTln(V_f/V_i)=∆q^ₛʸ^ₛ

∆S^ₛʸ^ₛ=nRln(V_f/V_i) in isothermal reversible expansion.

由於熵也是狀態函數,熵變量可以從可逆路徑的積分算得

考慮自然的事件視為一系統與參考系統(ex.熱儲)處於熱平衡(相同溫度),而自然事件往往是不可逆,其總共的熵變量會大於零; dS^ₛʸ^ₛ+dS^†≥0 or dS^ₛʸ^ₛ≥-dS^†, ⸪ dS^†=dq^†ᵣₑᵥ/T & dq^ₛʸ^ₛ=-dq^†ᵣₑᵥ

⸫ dS^ₛʸ^ₛ≥ dq^ₛʸ^ₛ/T Clausius inequality (若在封閉系統isolated system, 因為q=0, dS^ₛʸ^ₛ≥0)

宇宙看做一封閉系統,宇宙中有任何變化→∆S^univ≥0; 當宇宙處於熱平衡,使每個變化都是可逆→∆S^univ=0

ex. Consider a system taking round cycle in which state change from i to f by a irreversible path and return back to i along a reversible path. Check the integral of dq/T around the cycle

∮dq/T=∫ᵢ^ᶠdq/T+∫_fⁱdqᵣₑᵥ/T → ∮dq/T=∫ᵢ^ᶠdq/T-∫ᵢ^ᶠdqᵣₑᵥ/T=∫ᵢ^ᶠdq/T-∫ᵢ^ᶠdS=∫ᵢ^ᶠ(dq/T-dS) where dS=dqᵣₑᵥ/T

⸪ dS≥dq/T or dq/T-dS≤0, ⸫ ∮(dq/T) ≤0

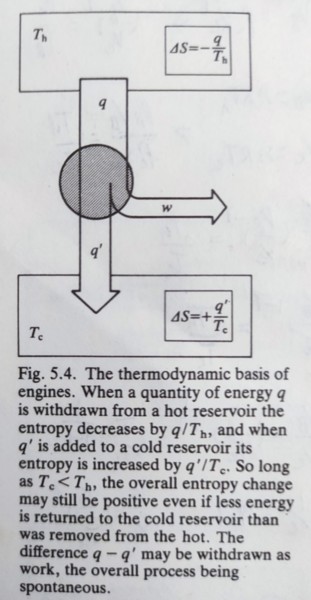
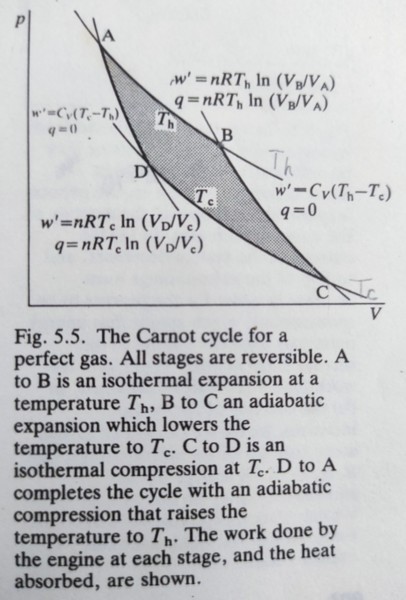
2^nd law: the entropy of an isolated system inceases in the course of a spontaneous change.

宇宙在此指系統與其周圍環境,看成一封閉系統

如何在不同條件計算系統的熵變量,由dS^ₛʸ^ₛ=dq^ₛʸ^ₛ/T,如果S(Tᵢ)已知, S(T_f)=S(Tᵢ)+∫ᵢ^ᶠdqᵣₑᵥ/T可積分得到

(i)常壓下加熱,(dqᵣₑᵥ)ₚ=dH=CₚdT, S(T_f)=S(Tᵢ)+∫ᵢ^ᶠCₚdT/T=S(Tᵢ)+Cₚln(T_f/T_i) if Cₚ與溫度無關

(ii)定容下加熱,(dqᵣₑᵥ)ᵥ=dH=CᵥdT, S(T_f)=S(Tᵢ)+∫ᵢ^ᶠCᵥdT/T

周圍環境的熵變量,不論可不可逆,只要視為一個保持熱平衡的熱儲, 若

(i)絕熱變化時, q^surr=0, ∆S^surr=0

(ii)常壓下一反應產生熱∆H, ∆S^surr=-∆H/T^surr ⸪ (q^surr)ₚ=-∆H, 可決定反應發生的方向

相轉變的熵: ∆ₜH是常壓下相轉變的潛熱(反應熱),在轉變溫度Tₜ時,系統與其周圍環境保持熱平衡(ex. 固液相在熔點時平衡,溫度也與周圍環境相同), 所以相轉變的熵變量∆S^ₛʸ^ₛ=∆ₜH/Tₜ

同時∆S^ₛʸ^ₛ+∆S^surr=0. 例如溶解和蒸發都是吸熱反應,系統的熵也會增加,正如我們所想: 氣相比液相亂度大,液相比固相亂度大

不可逆變化的熵: 熵是狀態函數, 無關於狀態之間的路徑

ex. isothermal expansion of a perfect gas from (V_i,T) to (V_f,T)

不管可不可逆,等溫膨脹的熵變量∆S^ₛʸ^ₛ=nRln(V_f/V_i);而周圍環境的熵變量必須視可逆與否: 可逆條件的熵變量∆S^surr=-nRln(V_f/V_i);若是絕熱條件,∆S^surr=0(⸪ q^surr=0).

ex. cooling: heat flow q from a hot body(Tₕ) to a cold(T_ᶜ), Tₕ>T_ᶜ

∆Sₕ=-q/Tₕ at hot source, and ∆S_ᶜ=q/T_ᶜ at cold block, ∆Sₜ=q/T_ᶜ-q/Tₕ>0; 當Tₕ=T_ᶜ時,∆Sₜ=0, 表示達到熱平衡

Carnot efficiency

從上例熱流可增加總體的熵(∆Sₜ>0),那麼我們只要維持∆Sₜ≥0,從高溫端流出的q抽走一部分,讓q流到低溫端,q-q的能量就可拿來做功. ⸪∆Sₜ=q/T_ᶜ-q/Tₕ≥0, q≥q(T_ᶜ/Tₕ) ⸫qₘᵢₙ=q(T_ᶜ/Tₕ)

因此wₘₐₓ=q-qₘᵢₙ=q[1-(T_ᶜ/Tₕ)], def: Carnot efficiency ε=wₘₐₓ/q=1-(T_ᶜ/Tₕ)

效率公式表示熱轉換為功的效率無法100%(除了T_ᶜ =0),例如內燃機燃油端有3200K,排氣端1400K,效率轉換為56%,但實際上其他損失會降至25%. 而且現實上低溫端cold sink無法接近零度,只能把引擎和渦輪的使用溫度提高

pf: state A→B at Tₕ, isothermal expansion process. ∆q=∆w=∫_Vᴀ^VᴃpdV=∫_Vᴀ^VᴃnRTₕdV/V=nRTₕln(Vᴃ/Vᴀ)

吸熱膨脹做功, Q₁=W₁=nRTₕln(Vᴃ/Vᴀ)

state B→C, adiabatic expansion process. ∆q=0, ∆w=∫_Vᴃ^VᴄpdV=∫_Vᴃ^VᴄK₀dV/V^γ=(1-γ)‪⁻¹(K₀/V^γ-1)|_Vᴃ^Vᴄ

=K₀/(1-γ)∙[1/Vᴄ^γ-1-1/Vᴃ^γ-1]=1/(1-γ)∙[pᴄVᴄ-pᴃVᴃ]=nR/(1-γ)∙[T_ᶜ-Tₕ]

⸪ pᴄVᴄ^γ= pᴃVᴃ^γ=K₀ and pᴄVᴄ=nRT_ᶜ and pᴃVᴃ=nRTₕ

絕熱膨脹做功, Q₂=0, W₂=nR/(1-γ)∙[T_ᶜ-Tₕ]

state C→D at T_ᶜ, isothermal compression process. ∆q=∆w=∫_Vᴄ^VᴅpdV=∫_Vᴄ^VᴅnRT_ᶜdV/V=nRT_ᶜln(Vᴅ/Vᴄ)

放熱壓縮被做功, Q₃=W₃=nRT_ᶜln(Vᴅ/Vᴄ)

state D→A, adiabatic compression process. ∆q=0, ∆w=∫_Vᴅ^VᴀpdV=∫_Vᴅ^VᴀK₀dV/V^γ=(1-γ)‪⁻¹(K₀/V^γ-1)|_Vᴅ^Vᴀ

=K₀/(1-γ)∙[1/Vᴀ^γ-1-1/Vᴅ^γ-1]=1/(1-γ)∙[pᴀVᴀ-pᴅVᴅ]=nR/(1-γ)∙[Tₕ-T_ᶜ]

⸪ pᴀVᴀ^γ= pᴅVᴅ^γ=K₀ and pᴅVᴅ=nRT_ᶜ and pᴀVᴀ=nRTₕ

絕熱壓縮被做功, Q₄=0, W₄=nR/(1-γ)∙[Tₕ-T_ᶜ]

In carnot cycle, at Tₕ end, Q₁=nRTₕln(Vᴃ/Vᴀ) 吸熱; at T_ᶜ end, Q₃=nRT_ᶜln(Vᴅ/Vᴄ) 放熱

總功Wₜ=W₁+W₂+W₃+W₄=nRTₕln(Vᴃ/Vᴀ)+nR/(1-γ)∙[T_ᶜ-Tₕ]+nRT_ᶜln(Vᴅ/Vᴄ)+nR/(1-γ)∙[Tₕ-T_ᶜ]

=nR[Tₕln(Vᴃ/Vᴀ)+T_ᶜln(Vᴅ/Vᴄ)]

ε=Wₜ/Q₁=[Tₕln(Vᴃ/Vᴀ)+T_ᶜln(Vᴅ/Vᴄ)]/Tₕln(Vᴃ/Vᴀ)=1+(T_ᶜ/Tₕ)ln(Vᴅ/Vᴄ)/ln(Vᴃ/Vᴀ)

=1-(T_ᶜ/Tₕ)ln(Vᴄ/Vᴅ)/ln(Vᴃ/Vᴀ)

e.g. pᴀVᴀ^γ= pᴅVᴅ^γ→ (pᴀVᴀ)Vᴀ^γ-1=(pᴅVᴅ)Vᴅ^γ-1→nRTₕVᴀ^γ-1=nRT_ᶜVᴅ^γ-1, T_ᶜ/Tₕ=(Vᴀ/Vᴅ)^γ-1

同理, pᴃVᴃ^γ=pᴄVᴄ^γ→ T_ᶜ/Tₕ=(Vᴃ/Vᴄ)^γ-1 ⸫(Vᴀ/Vᴅ)^γ-1=(Vᴃ/Vᴄ)^γ-1→ Vᴃ/Vᴀ=Vᴄ/Vᴅ

因此ε=1-(T_ᶜ/Tₕ)

ex. use Carnot cycle to determine the integral of dqᵣₑᵥ/T around a cycle is zero.

∮ dqᵣₑᵥ/T=Q₁/Tₕ+Q₃/T_ᶜ=nRln(Vᴃ/Vᴀ)+nRln(Vᴅ/Vᴄ)=nRln(VᴃVᴅ/VᴀVᴄ) i.e. Q₂=Q₄=0

⸪ T_ᶜ/Tₕ=(Vᴀ/Vᴅ)^γ-1, T_ᶜ/Tₕ=(Vᴃ/Vᴄ)^γ-1 ⸫ VᴃVᴅ/VᴀVᴄ=1, ∮ dqᵣₑᵥ/T=0

自由能函數, A & G(Helmholtz and Gibbs functions)

2^nd law告訴我們一封閉系統處於熱平衡(T^sys=T^surr=T),符合不等式: dS^ₛʸ^ₛ≥ dq^ₛʸ^ₛ/T

此不等式是以系統的函數表示自發變化的門檻,檢視以下的條件:

1. 當在定容下輸送熱,也沒有非pV功, (dq)_V=dU, 因此dS-dU/T≥0 or TdS≥dU

如果dU=0, (dS)_U,V≥0 or 如果dS=0, (dU)_S,V≤0

2. 當在定壓下輸送熱,也沒有非pV功, (dq)ₚ=dH, 因此TdS≥dH

如果dH =0, (dS)_H,ₚ≥0 or 如果dS=0, (dH)_S,ₚ≤0

自由能函數: A=U-TS, G=H-TS if state change at constant temp.,

dA=dU-TdS, dG=dH-TdS代入不等式, (dA)_T,V≤0 or (dG)_T,ₚ≤0

自由能不等式告訴我們一個系統在等溫定容下的自發變化必須(dA)_T,ᵥ<0;換言之,自發變化會降低自由能A, 而平衡的標準即是(dA)_T,ᵥ=0. dA=dU-TdS通常被解釋為系統狀態趨向於自由能比較低的狀態是因為系統低內能高熵所致,這是錯誤的! 2^nd law告訴我們整個封閉系統(系統+周圍環境)的熵≥0,其中包括系統的熵dS和周圍環境的熵dq/T, 所以dS是系統變化的熵,-dU/T是周圍環境變化的熵,兩個總和的熵趨向於最大值

Max. work: 自由能A也稱為功函數,將不等式dS≥ dq/T結合dU=dq+dw, 可得dU≤TdS+dw.dw是系統被做的功, 所以系統做功dw=-dw, dw≤-dU+TdS, 也就是說dwₘₐₓ=-dU+TdS=-dA

In the case of isothermal change, wₘₐₓ=-∆A=-∆U+T∆S

自由能G: 化學實驗通常在1大氣壓下進行,因此G函數在定壓下更常用,(dG)_T,p≤0的準則判斷化學反應朝自由能G減少的方向自動發生,直至自由能G達到最低,反應也才達成平衡,真實的反應驅動力是使整個封閉系統的熵變大

G=H-TS if state change at constant temp., dG=dH-TdS and dH=dU+d(pV)=dq+dw+pdV+Vdp

i.e. dq=TdS, dw=-pdV+dwₑ, dH=TdS+dwₑ+Vdp代入 dG=dwₑ+Vdp

at fixed p, dG=dwₑ 表示在定壓定溫下,自由能變化-∆G就是系統做的非pV功-dwₑ

第六章 第二定律機構

1^st & 2^nd laws的結合: dU=dq+dw(1^st law)對密閉系統的可逆變化而言, dw=-pdV and dq=TdS, 所以dU=TdS-pdV(6.1). dU是無關路徑的狀態函數,因此數學上符合exact differential.

不管路徑可不可逆,雖然TdS和-pdV隨路徑而變,但總和為dU,是無關路徑的狀態函數此種式子稱為基本公式. 假設系統的組成固定,可以基本公式開展各個性質的關係

dU=TdS-pdV應該視為S與V的函數, U(S,V);也可看作其他變數的函數, ex. U(S,p) or U(T,V),不過,當組成固定且無non-pV功的情況,U(S,V)是最好的、簡單的表示式,其微分式:

dU=(∂U/∂S)_VdS+(∂U/∂V)_SdV(6.2), → (∂U/∂S)_V=T, (∂U/∂V)_S=-p

由於(6.1)基本公式符合exact differential的特性

df=gdx+hdy is exact if (∂g/∂y)ₓ=(∂h/∂x)_y , ⸫ (∂T/∂V)_S=-(∂p/∂S)_V (6.3) i.e. g=T, h=-p

(6.3)稱為Maxwell relation

其餘的基本公式和Maxwell relation:

H=U+pV→ 微分式dH=dU+d(pV)=TdS-pdV+Vdp+pdV=TdS+Vdp (6.4), (∂T/∂p)_S=(∂V/∂S)_p (6.5)

A=U-TS→ 微分式dA=dU-d(TS)=TdS-pdV-SdT-TdS=-SdT-pdV (6.6), (∂S/∂V)_T=(∂p/∂T)_V (6.7)

G=H-TS→ 微分式dG=dH-d(TS)=TdS+Vdp-SdT-TdS=-SdT+Vdp (6.8), (∂V/∂T)_p=-(∂S/∂p)_T (6.9)

(6.1),(6.4),(6.6),(6.8)為基本公式, (6.3),(6.5),(6.7),(6.9)是Maxwell relation

ex. identify (∂U/∂V)_T=T(∂p/∂T)_V-p in the manipulation of the 1^st law.

Pf: dU=(∂U/∂S)_VdS+(∂U/∂V)_SdV → (∂U/∂V)_T=(∂U/∂S)_V(∂S/∂V)_T+(∂U/∂V)_S=T(∂S/∂V)_T-p

利用(6.7), (∂U/∂V)_T=T(∂S/∂V)_T-p=T(∂p/∂T)_V-p

ex. show thermodynamically that (∂U/∂V)_T=0 for a perfect gas and compute the value for a van der Waals gas.

Pf: p=nRT/V for a perfect gas, (∂p/∂T)_V=nR/V→ (∂U/∂V)_T=T(∂p/∂T)_V-p=nRT/V-p=0

p=nRT/(V-nb)-n²a/V² for a van der Waals gas, (∂p/∂T)_V=nR/(V-nb)

→ (∂U/∂V)_T=T(∂p/∂T)_V-p=nRT/(V-nb)-[nRT/(V-nb)-n²a/V²]=n²a/V²=a/Vₘ²

if van der Waals gas replaced by virial eq. p=(RT/Vₘ)(1+B/Vₘ+C/Vₘ²+...)

(∂p/∂T)_V=(R/Vₘ)(1+B/Vₘ+C/Vₘ²+...)+(RT/Vₘ)[(∂B/∂T)_V/Vₘ+(∂C/∂T)_V/Vₘ²+...]

→ (∂U/∂V)_T=T(∂p/∂T)_V-p=(RT/Vₘ)(1+B/Vₘ+C/Vₘ²+...)+(RT²/Vₘ)[(∂B/∂T)_V/Vₘ+(∂C/∂T)_V/Vₘ²+...]-(RT/Vₘ)(1+B/Vₘ+C/Vₘ²+...)=(RT²/Vₘ)[(∂B/∂T)_V/Vₘ+(∂C/∂T)_V/Vₘ²+...]=RT²(∂B/∂T)_V/Vₘ²+...

Gibbs函數的性質

由定義出發G=H-TS,可以導出基本公式dG=-SdT+Vdp是溫度與壓力的函數,因為一般的控制參數是溫度與壓力,Gibbs自由能在化學應用中很重要!

同理, (∂G/∂p)_T=V, (∂G/∂T)ₚ=-S 而且if dG is exact, (∂V/∂T)_p=-(∂S/∂p)_T

(i)溫度相關性: 由於(∂G/∂T)ₚ=-S和S為正的情況,當壓力與組成固定時,溫度上升時自由能降低,熵越大,自由能降得越快,所以氣體自由能對溫度敏感

將S=(H-G)/T代入(∂G/∂T)ₚ=-S → (∂G/∂T)ₚ=(G-H)/T or (∂G/∂T)ₚ-G/T=-H/T

(∂G/∂T)ₚ-G/T∂(G/T)/∂T, ⸪ [∂(G/T)/∂T]ₚ=(1/T)(∂G/∂T)ₚ+G[∂(1/T)/∂T]ₚ=(1/T)(∂G/∂T)ₚ-G/T²=(1/T)[(∂G/∂T)ₚ-G/T]

導出[∂(G/T)/∂T]ₚ=-H/T² (6.10) Gibbs-Helmholtz eq. 如果知道系統的焓H,也可以得到G/T 的溫度關係,(6.10)常用於物理狀態改變和化學反應: [∂(G_f/T)/∂T]ₚ-[∂(Gᵢ/T)/∂T]ₚ=-[(H_f/T²)-(Hᵢ/T²)], [∂(∆G/T)/∂T]ₚ=-∆H/T² (6.11) i.e. ∆G=G_f-Gᵢ and ∆H=H_f-Hᵢ, ∆G/T看起來是不好處理的數量

(ii)壓力相關性: (∂G/∂p)_T=V, 因為體積是正數,自由能與壓力成正比; G(p)=G(p)+∫ₚ^pVdp

若是固相或液相,V可視為常數, G(p)=G(p)+(p-p)V, 而且(p-p)V數值很小, ⸫G(p)≈G(p)

氣體的莫耳體積大,因此(p-p)V大且與壓力強相關,先以理想氣體為例

G(p)=G(p)+∫ₚ^pVdp=G(p)+nRT∫ₚ^pdp/p=G(p)+nRTln(p/p) 以標準狀態為參考值, p=p^⦵=1 bar

G(p)=G^⦵+nRTln(p/p^⦵) → Gₘ(p)=Gₘ^⦵+RTln(p/p^⦵) molar Gibbs function莫耳自由能

以純物質定義μ=Gₘ(p), μ=μ^⦵+RTln(p/p^⦵) chemical potential

真實氣體的有效壓力, fugacity: 為了處理偏離理想氣體的差異,以逸壓f取代p.

化學勢改寫為μ=μ^⦵+RTln(f/p^⦵) (6.12),首先建立f與p的關係: 利用G(p)=G(p)+∫ₚ^pVdp

→ ∫ₚ^pVₘdp=μ(p)-μ(p)=RTln(f/f) 真實氣體的情況,當壓力是p,氣體逸壓為f; 當壓力是p,氣體逸壓為f. 若是理想氣體(以°為記): ∫ₚ^pVₘ°dp=μ°(p)-μ°(p)=RTln(p/p), 前後相減

∫ₚ^pVₘdp-∫ₚ^pVₘ°dp=RTln(f/f)-RTln(p/p) or ln[(f/f)/(p/p)]=(1/RT)∫ₚ^p(Vₘ-Vₘ°)dp

當p→0, 真實氣體近似理想氣體,f→p:

因為p趨近零,f/p=1, ⸫ ln(f/p)=(1/RT)∫₀^p(Vₘ-Vₘ°)dp (6.13)

(6.12)可改寫: μ=μ^⦵+RTln(f/p)+RTln(p/p^⦵)

簡化(6.13): Vₘ°=RT/p for a ideal gas; Z=pVₘ/RT defined for a real gas and Vₘ=RTZ/p代入

→ ln(f/p)=∫₀^p(Z-1)dp/p or f=γp, γ=exp[∫₀^p(Z-1)dp/p] (6.14) fugacity coefficient

壓縮係數Z若小於1, 指數積分為負,那麼γ也小於1,即逸壓小於理想氣體的壓力(中低壓範圍吸引力主導);當Z>1,γ也會大於1,逸壓大於理想氣體的壓力(高壓時斥力主導)

ex. f determintion from van der Waals gas

RTdlnf=Vdp, dlnf=Vdp/RT → lnf|_f*^f=(1/RT)∫ₚ_*^pVdp, i.e. f對應p;f*對應p*(p*→0)

∫ₚ_*^pVdp=pV|_V*^V-∫_V*^VpdV= pV-p*V*-∫_V*^VpdV ⸪ p*→0, p*V*=RT

→ ln(f/f*)=[pV-RT-∫_V*^VpdV]/RT=ln(f/p*) → lnf=lnp*+[pV-RT-∫_V*^VpdV]/RT

p=RT/(Vₘ-b)-a/Vₘ²代入∫_V*^VpdV=∫_V*^V[RT/(V-b)-a/V²]dV=RTln[(V-b)/(V*-b)]+(a/V-a/V*)

⸪ p*→0, V*-b≈V* & a/V*→0

⸫ ∫_V*^VpdV=RTln[(V-b)/V*]+a/V=RTln[(V-b)/RT]+RTlnp*+a/V e.g. p*V*=RT

p=RT/(V-b)-a/V²→ pV= RTV/(V-b)-a/V→ pV-RT=RTV/(V-b)-a/V-RT=RTb/(V-b)-a/V

lnf=lnp*+[RTb/(V-b)-a/V-RTln[(V-b)/RT]-RTlnp*-a/V]/RT=b/(V-b)-ln[(V-b)/RT]-2a/RTV

lnf=b/(V-b)-ln[(V-b)/RT]-2a/RTV→ f=RT/(V-b)e^{b/(V-b)-2a/RTV}=γp i.e. p=RT/V

→ γ=V/(V-b)e^{b/(V-b)-2a/RTV} ⸫ lnγ=ln[V/(V-b)Gˋ]+b/(V-b)-2a/RTV

ex. pVₘ=RT(1+Bp+Cp²+...) virial eq., Z=(1+Bp+Cp²+...)

→ γ=exp[∫₀^p(Z-1)dp/p]=exp[∫₀^p(B+Cp+...)dp]=e^{Bp+Cp²/2+...} ⸫ f=pe^{Bp+Cp²/2+...}

ex. van der Waals gas p=RT/(Vₘ-b)-a/Vₘ², find the fugacity when attractive interaction ignored.

attractive interaction ignored, a=0, p=RT/(Vₘ-b) → Z=pVₘ/RT=1+pb/RT

∫₀^p(Z-1)dp/p=b/RT∫₀^pdp=pb/RT, f=pe^pb/RT

e.g. estimate its value for NH₃ at 10atm and 298.15K,

pb/RT=103.70710⁻³/(0.08206298.15)=0.015, f=10e^0.015=10.15atm

真實氣體的標準狀態: 假設如理想氣體的標準狀態, 當f=p^⦵, (6.12)可寫成μ=μ^⦵+RTln(p/p^⦵)+RTlnγ 前2項是理想氣體的化學勢,最後1項是理想氣體的偏差值

開放系統Open system: G除了有關溫度與壓力,組成變化也有關; G(p,T,n₁,n₂,...)