字體:小 中 大
字體:小 中 大 |
|
|
|
| 2009/12/03 01:27:16瀏覽13709|回應18|推薦103 | |
|
一張薄膜往四方無限撐開、拉大,它遲早要破裂。做為我們宇宙萬物存在背景基礎的空間本身,是可以向四面八方無限擴張的呢,還是一旦超過某個限度也會破裂開來?如果前者為真,空間為什麼會有這種性質?若是後者為真,裂開的空間又是什麼東西?
廣義相對論的公式穩固地根值在「黎曼幾何」的基礎上。
黎曼幾何假設,或者說要求,空間必須是「平滑無瑕」的,沒有皺摺、溝槽、穿孔、疊頁,當然也不可以有任何破裂的部分,否則「距離」一詞即無意義。兩點之間的距離是幾何裡最根本的要素之一,如果連距離都失去意義,幾何也就不成其為幾何了。 不止於此。空間的幾何形貌若非平滑無瑕,相對論的公式將立刻崩解,服膺相對論的宇宙不就要完蛋大吉了嗎?但事實上宇宙自始至今似乎運作無礙,一切正常。所以可見我們宇宙的空間實質上的確是平滑無瑕、完美無缺的吧? 其實不然。大舉成功的量子力學早已告訴世人,在極短小的距離範圍內,暴亂的時空劇烈動盪,有如近距離觀測波濤洶湧的海洋,無或稍息。
而這現象早已讓科學家們懷疑,宇宙時空的撕扯、碎裂、匯聚、癒合,可能根本就是隨時隨地都在發生的普遍正常現象,一如海面上的浪花,分分秒秒都在進行著同樣的聚散離合。
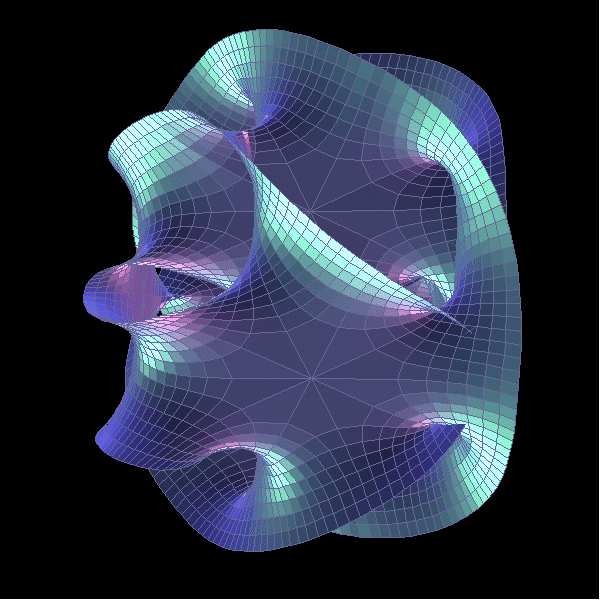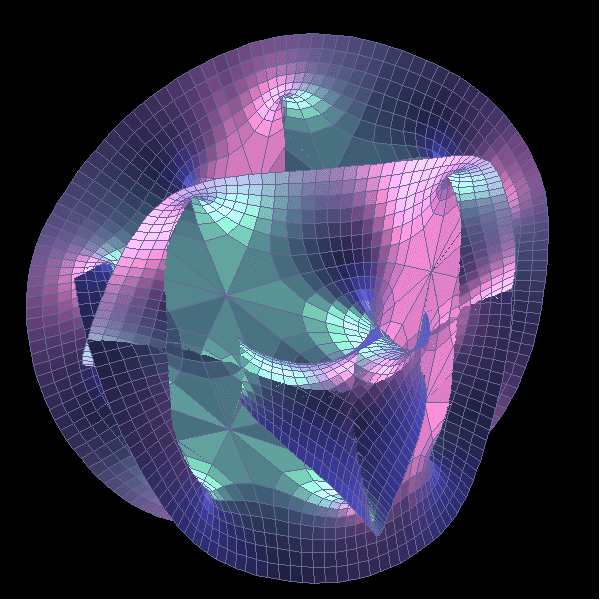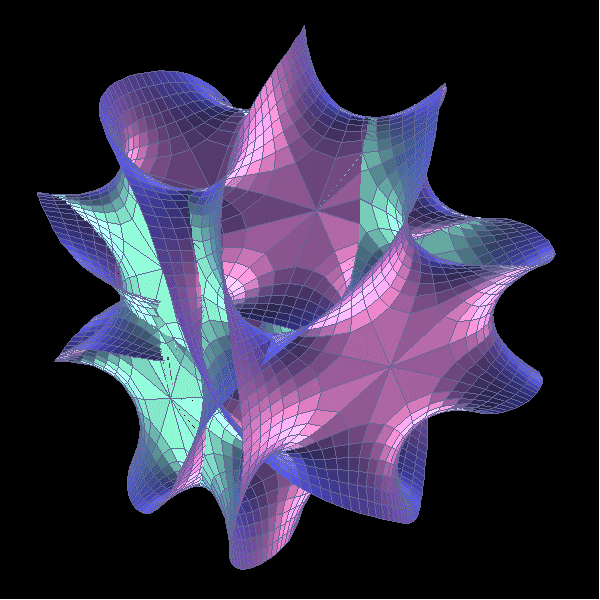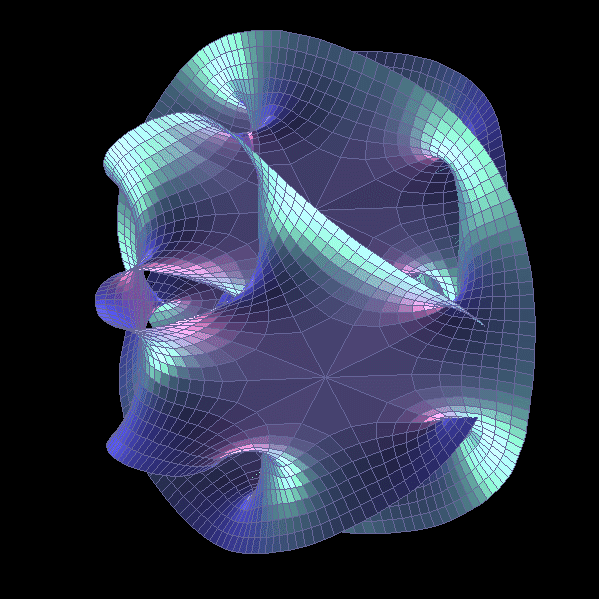
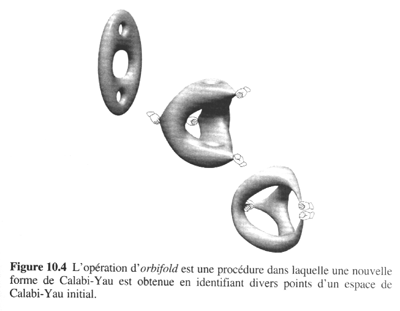
在此讓我們先把結論說出來吧:宇宙的空間理論上是可以被撕裂,再癒合的。本文試圖以最淺顯的文字交代達成此一研究結果的來龍去脈。但實際上又是如何?大家看完後可以自行揣摩,畢竟實驗觀測還不可能,任何答案都無所謂對錯。 1987 年間,丘成桐和他的研究生田剛,在某些卡拉比‧丘流形裡發現一種二度空間的球狀體。下為卡拉比‧丘流形示意圖:
球體不希奇,大家都知道是什麼。所謂「二度空間」的球體指的是一種類如海灘球表面,沒有厚度,沒有內在空間,純粹只有表面積,沒有所謂體積的這麼一個東西。丘和田試圖將此球體「縮小」至一個點,也就是零表面積,空間因此在該處被「掐斷」,一如一團麥芽糖用兩手拉開,中央部分越來越細,最後終於斷裂一樣。 他們接著在該斷裂處「補上」另一個新的二度球體,然後將它「膨脹」到原來大小。
這個「手術」的名稱叫做 "flop transition"。他們發現,經過 flop transition 的卡拉比‧丘流形與原先的卡拉比‧丘流形在拓樸學上為互異體。記得上篇提到過,甜甜圈和馬克杯為何互為拓樸學上的同形體嗎?因為我們不必撕裂麵團,就可以將甜甜圈逐漸揉搓捏弄成一個馬克杯。
以此,經過 flop transition 的這一前一後兩個卡拉比‧丘流形,在「手術」的過程中,必定曾經將空間撕裂開來。雖說在此我們用了幾個相當具象的動詞,譬如縮小、掐斷、補上、膨脹等等,然而一切都只不過是抽象的數學運算而已。真的空間會像這些描述那樣,實際上進行此種「手術」,從「之前」的狀態,經過空間的斷裂、修補,發展到「之後」的狀態嗎? 當丘成桐和田剛在 1987 年發表空間裂變的的初步假設時,不太有人以之為然。【量子幾何驚奇 ─ 弦論如何顛覆傳統距離觀﹝弦論六﹞】文中敘述的,1984年間 Keiji Kikkama 和 Masami Yamasaki 的發現:『當一個距離「縮小到普朗克值,再繼續微縮下去」時,一切所有物理現象正好和「縮小到普朗克值,然後開始增長上去」一模一樣,毫無差別。』已經成為弦論圈裡的通識﹝Planck length, denoted ℓP, is a unit of length, equal to 1.616252(81)×10−35 meters﹞。不過,在量子幾何裡,一個維度縮陷到小於普郎克距離的情形並不完全適用於一個空間崩塌時的狀況,因此布萊恩‧格林對丘成桐與田剛的結論雖不以為然,仍不免念茲在茲地不時懸想著。 1991 年,挪威物理學家安迪‧路肯與保羅‧阿斯蘋瓦爾提出一個有趣的命題:如果一個卡拉比‧丘流形內部的空間歷經前述 flop transition 的撕裂「手術」,從該流形的鏡對稱卡拉比‧丘流形看起來會是什麼樣子? 鏡對稱的發現者格林和普雷瑟在從事 orbifolding﹝orbifold 是 manifold ─ 流形的統稱,參【弦論七】﹞
的研究過程中,並未發現歷經撕裂的空間有何災難性的異狀發生。受到路肯和阿斯蘋瓦爾想法的鼓舞,他們發現可以用兩種方法「修復」一個裂變的空間:一種使撕裂點縮陷至零的二度球體回復原狀,另一種讓它走完 flop transition 全程,一如第四張圖由上至下所示。 截至 1991 年底,已經有不少學者認為,空間確實可能裂變。問題是無人有足夠的技術能力為空間裂變的可能提出支持或反對的證據。 格林和普雷瑟於 1992 年間力圖為空間裂變找尋證據,二人並在赴普林斯頓訪問時受到弦論大師惠登的加持。他們並與杜克大學的數學家大衛‧莫理森共同擬定一項證明空間裂變的「攻堅策略」。但是當三人坐來討論所須進行的數學運算時,他們發現,即使用全球最快速的電腦運算一個世紀也不可能完成。 就在此一困頓時刻,愛森大學的數學家維特‧巴特耶夫的研究成果為他們帶來一線曙光。 維特‧巴特耶夫一直以來對格林和普雷瑟二人找出卡拉比‧丘鏡對稱流形的物理方法迷惑不已,身為數學家的他於是便著手進行以數學方法構建鏡對稱流形的配對工作。巴特耶夫受到臺灣數學家阮希石的啟發,找到建立卡拉比‧丘流形配對的數學方法,並證明該法邏輯正確、有效可行。 布萊恩‧格林和其他物理學家一樣,對巴特耶夫的數學方法雖有信心,卻因不瞭解而頗感迷惑。他於是決定暫時離開康奈爾,到普林斯頓高等研究所去,準備以一個秋季的時間在那裡和同樣也要去普林斯頓的莫理森及阿斯蘋瓦爾,三個人一起來解決空間裂變的難題。 他們很快的發現,要直接解決這個 flop transition:
的數學問題是不可能的,變通的辦法是改採上面這九個步驟的鏡對稱流形來解。好消息是,改頭換面之後的流形不再有中心點空間斷裂的現象,或許這意味著,原來的九個步驟在我們的宇宙空間中確實發生,並且無害也無礙地進行。問題之一是:變通的辦法還是須要證明,它的數學也未必見得就比較容易;二是:鏡對稱原理是否可以被拿來運用到如此極端的地步,甚至跨越到空間裂變的另一端,而依然正確有效? 簡單講就是,現在不但得在數學上算出變通辦法的每一個步驟,還得保證變通的辦法確實可以取代原來的所有步驟。 格林,莫理森,和阿斯蘋瓦爾 '92 年的整個秋天在普林斯頓搞的就是這些運算和證明。他們成功的故事精彩無比,也將是下篇【空間的裂變及癒合 ─ 答案是什麼?﹝弦論九﹞】的主要內容。
|
|
| ( 知識學習|科學百科 ) |