字體:小 中 大
字體:小 中 大 |
|
|
|
| 2014/01/21 16:03:11瀏覽7038|回應9|推薦45 | |
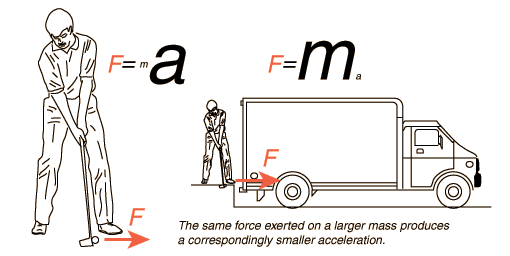
牛頓在十七世紀發表他的力學第二定律 F = m.a 意思是:作用在一個物體上的力(Force,F)產生一個相應比例的加速度(acceleration,a)。在這裡 m 是此物體的質量(mass,m),「.」在代數裡是「乘」,可省略,如 F = ma。 也就是說,如果一個物體沒有任何(淨)力作用於它,此物體將無加速度,它的速度守常不變(所謂靜者恆靜動者恆動,速度包括物體運動的方向和速率)。加速度的「加」不一定是加速,也可以是減速(負加速度),或方向的改變。 我們在坐轉轉馬時雖然繞的速率不變,但方向一直在變,所以有「加速度」,因此一定有一個力在作用。轉轉馬的「力」就是向心力。讓我們感覺不抓緊會摔出去的離心力是向心力的反作用力。 牛頓第二定律一直被用來解釋一個系統(譬如一顆飛行中的高爾夫球)的物理狀態和力學行為,並預測它在時間裡(包括過去和未來)將如何演變。
在量子(分子原子以及次原子等極微粒子)力學裡類似牛頓理論的方程式是薛丁哲方程式(Schrödinger's equation)。薛丁哲方程式不是一個簡單的代數方程,而是一個「線性偏微分方程式」,用來描述量子的「波函數」(wave function,其值就是「量子態」quantum state)。 既然說「類似牛頓力學第二定律」可見薛丁哲方程式必與時間有關。確實,所謂薛丁哲方程式對量子態的「描述」一如牛頓力學第二定律,它主宰波函數在時間裡的演變過程。這是量子力學的「公設」,此基本概念不從任何其他概念而來,it simply is。
波函數(如上圖,以 ψ 表示)是對一個物理體系所能給予的,最完整的描述。薛丁哲方程式對此體系的波函數解不但能夠描述分子、原子、次原子粒子的動態,甚至對宏觀物體像人、地球、乃至整個宇宙都可能正確描述。 所謂的「波函數」 ψ(r, t) 其值是一個「複數」,用來描述一個粒子和它(在空間時間裡)的行為,因此它的值是空間和時間(r 和 t)的函數,也就是說會隨空間時間的不同而改變。
複數是一種比較複雜的數字,由實數(譬如 1,2,3 等)和虛數(imaginary unit,所以用 i 表示,等於負一的平方根)合成,像 a + bi。在這裡 i2 = −1。由於沒有那種數目的平方(自己乘上自己)是負的(所謂負負得正),所以這個自乘後變 −1 的數字叫虛數。因為“1”,所以叫「單元」(unit)—— i,就是虛數裡的 1。 波函數的值如果畫成圖像看起來呈波浪狀,因得此名。雖然波函數的值是個(連實帶虛的)複數,它的絕對值平方(|ψ|2)是實的(記得 i2 = −1,−1 是負的實數)。這個 |ψ|2 的值代表「在某時某處可找到某粒子的或然律」,也就是說,它某時某刻出現在某處的可能性。意思是說,在某特定時候,一個粒子可能出現在任何地方,無所謂「一定會」或「絕對不會」,只有可能性的大小。數學語言的講法是:一顆粒子的波函數絕對值平方對一個三度空間區域的積分值是一個無單位的概率,代表此粒子出現(存在)在此區域(所以要積分)的可能性。
波函數和薛丁哲方程式是量子力學的中心理論,也是對粒子運動最直接、最徹底的描述。雖然波函數蘊藏粒子的行為資訊,它並不(像牛頓力學第二定律那樣)給出一個粒子或宏觀物體的任何可量度值(譬如速度,含方向和快慢,或位置)。要得到它們必須透過一種「量子算符」(quantum operator,或算子)作用在量子態 ψ(r, t) 上來獲得。數學上 operator 是「動詞」,像 2 X 3 = 6 裡的 X,把兩個值乘起來,作用和 + 不同,但都具有某種意義。
在上式中, I : H → H 以文字解釋的話,我們說一個算子 U 和它伴隨的反算子 U∗ 聯合起來不論先後作用於一個量子態的結果將還原該量子態的本來狀態,相當於採用一個「恆等算子」I 的結果 —— 一切如常,nothing happened。而 I 這個算子之所以叫「恆等」是因為它像回音,你給它什麼它還你什麼,等於無作用。 U 和 U∗ 很厲害的,可作用在多度乃至無數度空間,結合向量幾何和微積分應用在歐基里德空間裡的方法。一個把東西「轉換過去」,另一個再把它「還原回來」,所以恆等(I 是 Identity,即「自己」、沒變)。 整個來說就是,以算子 U 和它伴隨的反算子 U∗ 在一個多度空間(所謂西爾伯特空間,Hilbert space,所以 H)裡先後作用在某量子態 ψ(r, t) 上的結果應該完整還原該量子態 ψ(r, t)。 量力的「算符」是一種「么正(unitary)算符」。么什麼么?么這個:么 => 一 => uni。我是為了寫這篇才去查各個詞的中文翻譯,結果發現,現在專有名詞的英翻中幾乎都被大陸壟斷了,所以才「么」。要換我來翻,我才不會翻得這麼肉麻,我會翻成「歸元算子」。
么正(unitarity)的意思是這樣的:在一個量子系統內某單一事件所有一切可能結果的或然率加起來的總和必須等於 1(「么」是「一」,「正」是「整」,像我們說「新臺幣一萬元整」的整)。這是一個「規定」,沒有為什麼。比方說,一間屋子裡如果有一個橘子,這橘子可能在餐桌上,可能在冰箱裡,即使被我吃掉不見了,在我肚子裡還是在這間屋內,無論如何每一種可能性都小於一,但全部加起來必須、也一定等於一,就是說「橘子一定在屋裡」。很多東西都「么正」,或然率么正,百分比也么正。拿百分比來比喻就更清楚了。我們說總共一百顆(有黑有白的)球裡白球的百分比如下: 1 白,99 黑:1% = 0.01 5 白,95 黑:5% = 0.05 77 白,23 黑:77% = 0.77 100 白,0 黑:100% = 1
沒有什麼叫做 123% 這種事,百分比也「么正」,100% 等於 1。
既然一個系統的全部資訊「含藏」在它的波函數裡,此資訊在某一時間點上的狀態應該完全可以決定它在其他時間點上的狀態。而作用在波函數上的么正算符「保證」從量子角度而言資訊將永遠被完整保存,只是從一個狀態(在時間裡)演變成另一個狀態,不會憑空消失。記得嗎?U:H --> K,U∗:K --> H。量子態可以轉變,也必須可被還原。U 把量子態 H 轉變到 K,U∗再把 K 還原回 H。你的手機正面朝上放在桌上,這是量子態 H,將它翻轉過來正面朝下,這是量子態 K,有「回不到量子態 H,手機再也無法正面朝上」這種事嗎?當然沒有。再翻一次不就回到原狀了? 之所以要講這麼多的理由在這裡: 量子力學裡的量子態(即波函數值)連同它們的么正算符,加上詮釋波函數如何演繹的薛丁哲方程式,構成最嚴格的「決定論」(determinism),叫「量子決定論」(quantum determinism)。
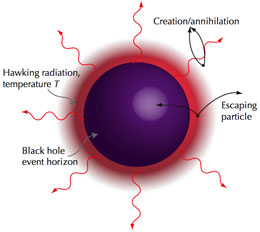
事情彷彿一片大好,直到資訊悖論(information paradox)出現。 1974 年,英國物理學家史蒂芬.霍金(Stephen Hawking)發現(注:算出或預期,不是觀測)黑洞會輻射(叫霍金輻射),差不多同時間貝肯斯坦(Jacob Bekenstein)發現黑洞有溫度和熵。黑洞會輻射,經過一段很長的時間還會因輻射而損失物質過多最後從宇宙裡「蒸發」掉?黑洞不是有進無出,連光都逃不出來的嗎?加州理工的基普.松(Kip Thorne)有一本名著叫「黑洞與時間擰扭」(Black Holes and Time Warps,留在美國家裡沒帶來,不然我就可以轉載),裡頭對霍金輻射有詳盡解釋,在此暫按不表。大強子對撞機可能打出的微黑洞專家們咸認沒有危險,就是因為它們即便被打出來也會在極短時間內霍金輻射到完全「人間蒸發」。
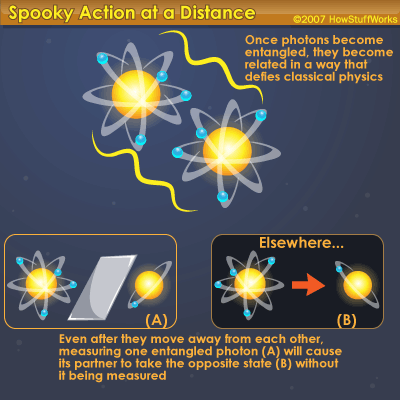
霍金不但發現黑洞會「蒸發」,更發現蒸發掉的黑洞不會保存它之前吞食掉的所有資訊。今天的全像宇宙論者多以為霍金是錯的,而後者在 2004 年承認自己的想法有誤,資訊不從宇宙消失。即便被黑洞吞食後又蒸發掉,之前發生的事情也都還在,必定保存在某處(其實就是黑洞事界),這是全像宇宙論的看法。 霍金認為宇宙資訊會因黑洞而憑空消失的理由和所謂「量子糾纏」(quantum entanglement)有關。量子糾纏是一種已獲證實的奇異現象:一對(如雙胞胎般)一起產生的粒子其中的一顆它的量子態將永遠和另一顆息息相關,二者間的距離彷彿不存。也就是說,一顆有變另一顆也會立即改變,觀測一顆等於同時觀測另一顆,不論二者距離多遠 —— 它們之間的「心電感應」所需時間是零,比光速還快(現今實際測量值高於光速一萬倍 —— 一般咸信這是儀器問題,其速應為無限大,真正「同時」),好像兩顆是同一粒子、還在一處,宇宙沒有距離這回事。
霍金假想,在黑洞事界上產生的一對粒子,一顆墮入洞內,另一顆逃逸變成黑洞輻射。而墮入黑洞的那顆都消失在黑洞奇點裡了,還能與外在那顆怎麼繼續「糾纏」?也就是說,我們難道還能從逃逸掉的那顆得知消失了的那顆的量子態不成? 霍金不以為然,認為墮入黑洞那顆的量子態即便 after 此黑洞完全蒸發掉也回復不來,整個的從宇宙消失,它的量子態資訊不見了!他正式宣告資訊不滅論因黑洞而破功,因為你無法以 U∗ 回復它過去的量子態。霍金的結論惹惱了很多人,但苦於無計反駁這位物理大師,因為你必須解釋黑洞如何保全資訊,而霍金的論述又滴水不漏到無懈可擊,一直到全像原理面世。全像原理的反撲最終讓霍金承認錯誤,並於 2004 年發表他以為的,黑洞事界保存宇宙資訊不讓量子決定論破功的原理。 「資訊悖論」所指在此 —— 資訊不應從宇宙消失,no matter what。說資訊會自宇宙消失得無影無蹤,即便是透過變態到將宇宙時間、空間扯到破的黑洞也讓人無法接受,所以叫「悖論」。下篇文章將敘述全像原理的絕地大反撲 —— 它解釋黑洞事界如何保存宇宙資訊,並將此原理推廣到宇宙本身的經過。 |
|
| ( 知識學習|科學百科 ) |




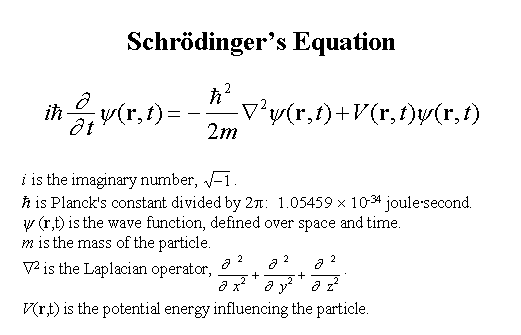
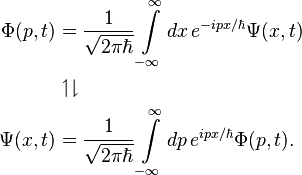


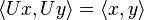
 決定論說,每一件事情都存在有許多條件,而這些條件無法造就出任何其他事情。一隻蝴蝶搧一下翅膀或不搧,後果將是兩種截然不同的宇宙未來走向。在蝴蝶搧一下的宇宙裡可能形成蝴蝶不搧的宇宙裡不存在的一場颱風,這就是有名的「蝴蝶效應」(butterfly effect)。蝴蝶效應的原理正是決定論。如果蝴蝶搧一下的宇宙和沒搧一下的宇宙之後完全相同,決定論就破功。在量子論裡,么正算符暗喻著絕不破功的「量子決定論」—— 一個波函數未來的演變完全由它的算符決定,而這個算符的反算符同樣地也能從新波函數反推回過去的那個舊波函數。你可以說,
決定論說,每一件事情都存在有許多條件,而這些條件無法造就出任何其他事情。一隻蝴蝶搧一下翅膀或不搧,後果將是兩種截然不同的宇宙未來走向。在蝴蝶搧一下的宇宙裡可能形成蝴蝶不搧的宇宙裡不存在的一場颱風,這就是有名的「蝴蝶效應」(butterfly effect)。蝴蝶效應的原理正是決定論。如果蝴蝶搧一下的宇宙和沒搧一下的宇宙之後完全相同,決定論就破功。在量子論裡,么正算符暗喻著絕不破功的「量子決定論」—— 一個波函數未來的演變完全由它的算符決定,而這個算符的反算符同樣地也能從新波函數反推回過去的那個舊波函數。你可以說,