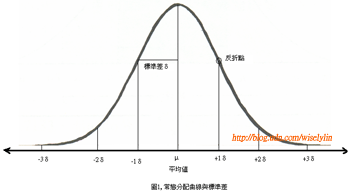
統計學中常以常態分佈曲線(Normal Distribution)來描述一個流程或母群體之可量測特性(Measurable Characteristics)的隨機行為(Random behavior)。在實務上也廣泛應用在企業與產業界，如產品的特性、化學與電子等。

常態分佈曲線如圖所示，主要特性為出現次數最多之處即為平均值，而平均值的左右兩邊曲線為對稱，反折點與平均值之距離，即為一個標準差(δ)，曲線由平均值的兩側往下滑，尾部永不與水平軸相交。

如果X代表產品品質的特性變數，當產品品質特性可以使用常態分佈曲線描述時，樣本變數之平均值也可用常態分佈曲線來表示。而標準差就可以用來量測樣本平均值的變異程度。常態分佈曲線可以用標準差來劃分標準差區域，曲線下的面積就代表平均值出現於兩點之間的機率。一個平均值(μ)的標準差面積為0.6827，即表示出現在此區域之機率為68.27%，出現在者區域之外的機率為31.73%。

μ±1δ：68.27%

μ±2δ：95.45%

μ±3δ：99.73%

μ±4δ：99.9937%

μ±5δ：99.999943%

μ±6δ：99.9999998%