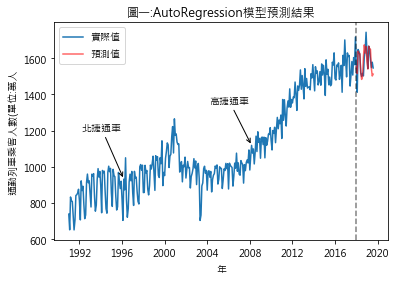
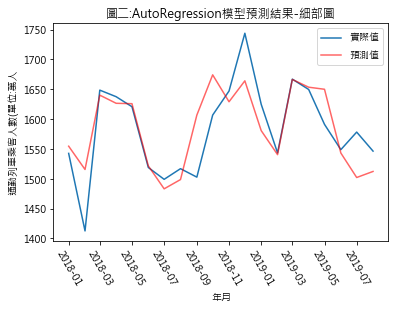
<<Python練習  時間序列的自我迴歸(Autoregression)>>

一、依過去的資料預測未來 – 時間序列的直覺

看著時間序列圖形,我們常不禁好奇,現在的走勢是否會延續至未來?先前練習的Naïve(天真)預測法可說是此種思維下的一種極端例子:「未來=現在」,未來一律等同目前的情況.

既然未來與過去有關,那麼若我們能找出未來與過去之間的關係,我們即能利用過往的資訊來預測未來,自我迴歸(Autoregression,AR)即是此種想法下發展出的預測模型.延續先前台鐵通勤列車乘客人數預測的練習,圖一及圖二是運用AR模型得出的預測結果,其與實際數據間的擬合程度雖優於先前練習的Naïve及Snaïve預測法,但其過程則曲折多了.

二、自我迴歸(Autoregression,AR)模型

AR是統計上一種處理時間序列的方法,用同一變數,例如X的之前各期,亦即用X_1期至X_t-1期來預測本期X_t期的表現,並假設它們為一線性關係,簡單說,就是用自己來預測自己.

X_t = a + b_t-1*X_t-1 + b_t-2*X_t-2 + … + b_2*X_2 + b_1*X_1 +ɛ_t

三、前世情緣 – 一段曲折的路

AR模型雖簡單易懂,但在適用上有其先天限制,即用來預測的資料集數據本身,需具有穩定性(stationary).

(一)穩定性(stationary)定義

是指資料集數據的統計屬性(如平均數或變異數等),不會隨著時間流動而有波動改變.至於如何判定資料集是否具有穩定性,則需要使用上有如有字天書的統計技巧.

(二)Python中用來判定穩定性的方法及套件

1.統計方法: 使用Augmented Dickey-Fuller (ADF) 檢定法(別問我這是什麼鬼東西)

2.匯入套件: from statsmodels.tsa.stattools import adfuller

3.語法: 檢定結果 = adfuller(資料集)

4.檢定結果:會帶二項統計資訊

(1)ADF統計值,及1%、5%、10%臨界值

(2)p-value

5.資料集穩定性評斷基準

(1)ADF統計值 < 臨界值

(2)p-value < 0.05

(三)通往穩定性的曲折之路

1.延續先前的季節性因素分離練習,首先檢驗抽離出的通勤列車趨勢值(trend),結果未通過ADF檢驗,即通勤列車趨勢值本身不具備穩定性,須動些手腳,讓資料能具有穩定性,才能使用ＡＲ

2.如何讓資料變成具有穩定性

有些方法可嘗試讓資料具有穩定性,但不是絕對的,仍須看最後的統計檢定結果.

(1)   差分:計算每一期通勤列車趨勢值與上一期通勤列車趨勢值的差額,再計算這些差額數列是否具有穩定性

1. Python語法: 差分數列 = 原始數列.diff()
2. 統計結果: ADF檢驗仍未通過

(2)   對數:對通勤列車趨勢值求其自然對數,再看這個對數數列是否具有穩定性.

i.Python語法: 對數數列 = numpy.log(原始數列)

ii.統計結果: ADF檢驗仍未通過

(3)   對數差分: 計算每一期通勤列車趨勢值對數值與上一期通勤列車趨勢值對數值的差額,再計算這些對數差分數列是否具有穩定性

1. Python語法:對數差分數列 = 對數數列.diff()
2. 統計結果:皇心不負苦心人,總算通過ADF檢驗

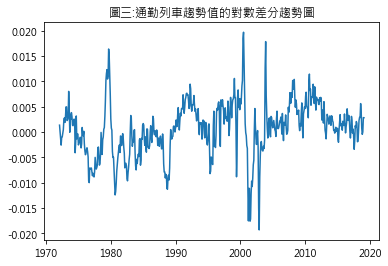
ADF Statics: -3.412633

p value: 0.010536

Critical Values:

    1%: -3.442

    5%: -2.867

10%: -2.570

圖三為通勤列車趨勢值的對數差分趨勢圖,從肉眼無法看出所謂穩定性的圖形規則特徵.

四、三生三世的糾纏 - 本期結果受前期資料的影響度

明日的我,會受昨日的我的影響,大家沒有多大的疑義.但若說七世前的我,仍對明日的我有極大的影響力,縱使相信輪迴之說,或許會對此說法打上問號.通常來說,愈久遠的數據,對未來的影響力應呈遞減狀態,所以AR模型雖簡單易懂,但在運用前要先回答一個問題:多久前的資料,仍對未來具有顯著影響力?在統計學上,這稱為自我相關(autocorrelation).

(一)自我相關(autocorrelation)定義

將一個有序的隨機變數序列與其自身相比較，如果序列中的組成部分相互之間存在相關性（不再是隨機的），所得的自我相關值的範圍在-1至1之間,1為最大正相關值，-1則為最大負相關值.但若不存在相關性,則自我相關值為0.

(二)Python中有關autocorrelation的視覺化圖形

1. 1.      pandas.plotting.autocorrelation_plot(時間數列)

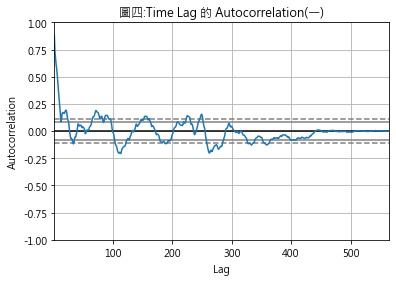
圖四為通勤列車趨勢值對數差分數列按此法畫出的圖形.橫軸為遞延期數,愈右邊,代表愈久遠的資料.縱軸為自我相關係數,顯示各期遞延資料對本期資料的影響程度.

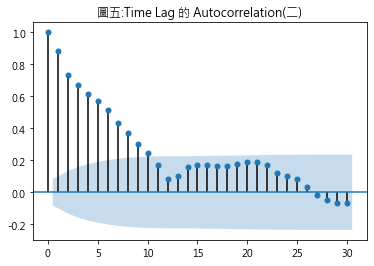
在圖形上可看到一對平行的虛數及實數,虛數代表統計上99%信賴區間的臨界值,實線則是95%信賴區間臨界值.自我相關係數位於虛線或實線之外,代表具有統計上顯著性,反之,則不具有統計上的顯著性.

從圖四可看出,自我相關係數隨著遞延期數迅速下降呈狹幅波動線形且不具統計顯著性,符合愈近的資料,對目前結果愈具影響力的直覺觀點.

2. statsmodels.graphics.tsaplots.plot_acf(時間數列,遞延期數)

plot_acf()一樣可視覺化自我相關係數與遞延期數之間的關係,只不過該法須事先指定遞延期數的範圍.從圖四結果可知,愈遠的期數已不具影響力,故我們將遞延期數訂為30,圖五為得出的圖形.橫軸與縱軸代表的意義同圖四,圖形上有層陰影區,自我相關係數若落在陰影區裏,即代表不具有統計顯著性.從圖五可看出,遞延期數若大於10,則不具有統計顯著性.

五、醜媳婦見公婆 – AR模型預測結果

在Python,我們可使用statsmodels.tsa.ar_model.AR套件來建構AR模型進行預測

(一)匯入套件: from statsmodels.tsa.ar_model import AR

(二)建構AR模型及其預測過程

1. 訓練資料集(train data set):為1972年1月至2017年12月,各月的通勤列車趨勢值的對數差分數列,以下簡稱為對數差分訓練集.
2. 2018年1月至2019年8月的通勤列車趨勢值的對數差分預測,以下簡稱為對數差分預測

(1)   建立AR模型: 模型 = AR(對數差分訓練集)

(2)   訓練模型: 訓練後模型 = 模型.fit()

運用AR模型時,遞延期數的指定是至關重要的. statsmodels.tsa.ar_model.AR套件提供一項貼心的功能,函式本身會自動幫我們挑選最適遞延期數,我們不用為此傷腦筋.我們若想知道AR模型訓練後選定後的遞延期數是多少,可使用

訓練後模型.k_ar

這道指令查看.這次練習例子,AR模型選定的遞延期數為18期.

(3)   對數差分預測結果 = 訓練後模型.predict(start=datetime(2018,1,1), end=datetime(2019,8,1))

start及end這二個參數,是用來設定預測資料的起迄日期.

3.導出通勤列車的2018年1月至2019年8月的乘客人數預測值

目前求出的是對數差分預測值,並不是我們想要的結果,我們需再進行下列步驟:

(1)   利用模型求出的對數差分預測值,得出各期對數預測值

t值對數值 = (t-1)期對數值 + t期對數差分

(2)   將各期的預測對數值,還原成一般值

通勤列車趨勢值預測 = numpy.exp(對數預測值)

(3)   通勤列車乘客人數預測

t期通勤列車乘客人數預測 = t期通勤列車趨勢值預值 + t期季節因素

圖一及圖二,即預測值與實際值的視覺化比較結果

(4)預測效果:RMSE的檢驗結果為47.96,優於先前練習的Naïve及Snaïve預測法.