<<Python練習  時間序列數據的季節性因素分解>>

一、時間序列與季節因素

時間序列(time series) 是一組按照時間發生先後順序進行排列的數據點序列,在長期觀察下,有時時間序列數據似乎沿著某種長期趨勢演進發展,若能界定出此種長期趨勢,即能依照現在及過往的觀察數據對未來進行預測。

通常觀察一組時間序列數據時不會呈現一條平滑的曲線,而是峰谷間上下來回波動,而再深入觀察,會發現此種上下來回波動的現象,常週期性地規律重複發生,我們將這些造成數據定期波動的外在因素稱為季節性因素(seasonality),我們如能將季節性因素所造成的數據上下波動假象移除,即能掌握住時間序列的長期趨勢動向.

二、時間序列數據的分解

依照上述思維,我們可將一組時間序列分解為由下列三種因素組合而成:

(一)趨勢(trend): 影響時間序列長期走勢的基本動因.

(二)季節性因素(seasonality): 造成定期性規律波動的影響變因.

(三)噪音(noise): 無法用以上二種因素解釋的變因.

三、由時間序列分解出季節性因素

如何從時間序列數據中分離出季節性因素,現有不少作法,不同的作法有其先天假設及限制,需依照數據本身特性選擇適當的方法,這是事先需銘計在心的.我這個初學者,先練習一個在1920年代發展出來,較簡單(反義即是對數據的限制要求較多)的古典分解法(classical decomposition method),這個分解法可再分為二個分支:

(一)添加法(additive)

additive法是認為實際數據是由趨勢、季節性因素及噪音三者累加而成的,即

Y[t] = T[t] + S[t] + e[t]

Y[t]: t期時觀察值

T[t]: t期時趨勢值

S[t]: t期時季節性因素

e[t]: t期時噪音

additive法的背後假設,是趨勢、季節性因素及噪音三者對實際數據影響是呈線性(linear)關係.

(二)累乘法(multiplicative)

multiplicative法是認為實際數據是由趨勢、季節性因素及噪音三者累乘而成的,即

Y[t] = T[t] * S[t] * e[t]

multiplicative法的背後假設,是趨勢、季節性因素及噪音三者對實際數據影響是呈非線性(non-linear)關係.

本練習的目的,是利用一組時間序列數據,來評斷additive法、multiplicative法二者之中,何者較適宜處理練習數據集的季間性因素分離問題.

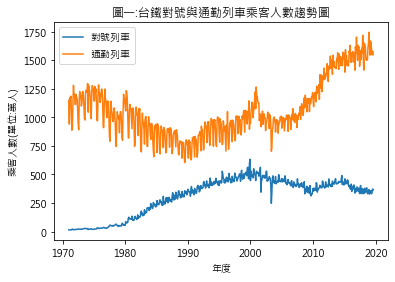
四、資料蒐集及整理

基於一名鐵道迷的好奇心,本次練習嘗試以台鐵歷年通勤列車(非對號列車)的乘客數為分析數據

(一)資料來源

1. 1.      下載路徑: 中華民國統計資訊網 > 全國統計資料 > 運輸、倉儲及通信業 > 運輸統計 > 台鐵客貨運統計 > 進一步查詢 > 臺鐵旅客列車客運概況
2. 2.      資料期間: 從民國60年1月至最近月份,下載當時為108年8月.
3. 3.      檔案格式: Excel檔

(二)資料清理

為便於後續能利用Python工具分析,資料需進行下列預先處理:

1. 1.      將Excel檔轉為csv檔
2. 2.      中文編碼,由BIG5,轉為utf-8
3. 3.      將資料匯入Python工作平台並轉為Pandas物件
4. 4.      資料內容按年月依序排列,但每年有當年度小計資料,為便於資料分析時能按逐月趨勢分析,須將這些年度小計資料找出並刪除
5. 5.      原始資料的時間是民國年、月,為便於能直接使用Python的套件來分析,需將民國年、月轉為西元年、月,並將資料格式變為Timestamps型態
6. 6.      原始資料,分為”自強號”、”莒光號”、”區間列車”及”普通車”.因”自強號”、”莒光號”主要為長途旅客,合併為”對號列車”, ”區間列車”及”普通車”的旅客主要為短期通勤,合併為”通勤列車”.

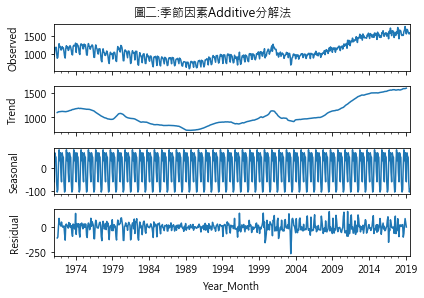
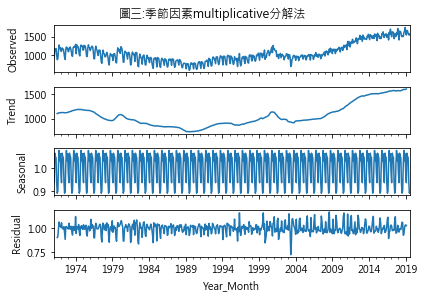
五、季節性資料分解

依前所述,本練習將採用古典分解法來分解季節性因素.

(一)套件匯入

from statsmodels.tsa.seasonal import seasonal_decompose

(二)語法

DecomposeResult物件 = seasonal_decompose(Pandas物件,model=additive(multiplicate))

其中參數model=’additive’時採用additive分解法;若是model=’multiplicative’,則是’multiplicative’分解法.圖二及圖三分別為這二種方法分解後的情形,圖中四個小圖分別代表:

1. Observed:原始數據
2. Trend:趨勢值
3. Seasonal:季節性因素
4. Residual:噪音項

additive與multiplicative分解法得出的圖形外觀看似雷同,但二者實質意義不同,additive法是不同因素間相加,而multiplicative法則是相乘.

六、以預測結果評斷additive及multiplicative分解法

接下來,就要以預測結果來評斷additive及multiplicative分解法,何者較佳

(一)預測結果的評斷

將2018年1月至2019月8月這20個月的期間,設定為預測檢驗期,以這20個月的實際值,與預測方法得出的該期間預測值進行比較,來評斷何種方法較佳

(二)預測方法的選用

預測方法也是有多種方式可選擇,在此選用最簡單的Naïve(天真)預測法,即預測值直接等於過去的實際觀察值.此種方法雖然預測效果通常較不佳,但可用該法的預測結果作為標桿(benchmark),作為檢測其他較複雜方法的預測效能.

Naïve預測法,可再概分為二類:

1. Naïve法:預測期間每一期的數值都等於最近一期的實際觀察值,即

Ŷ(t+h|t) = Ŷ(t+h|t)

    Ŷ(t+h|t): t+h期時的預測值

    Ŷ(t+h|t): t期時的實際觀察值

由於我們已將數據分解為趨勢及季節因素二大部份,季節因素變動假設會再重複發生,我們故可僅對趨勢值進行預測.至於噪音,屬未知項目,無法對其預測.

(1)additive分解法

    t+h期預測值 = t期趨勢值實際值 + (t+h)期的季節性因素

            此例t期:指2017年12月

(2)multiplicative分解法

t+h期預測值 = t期趨勢值實際值 * (t+h)期的季節性因素

1. SNaïve法:預測期間每一期的數值都等於最近T期前的實際觀值,即

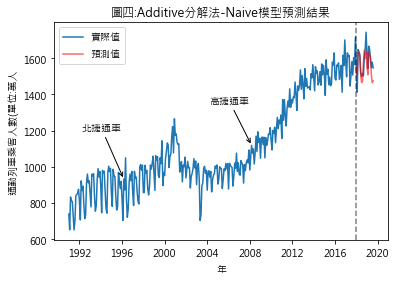
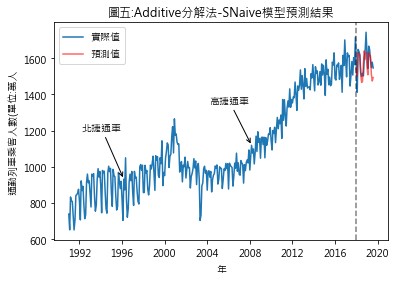
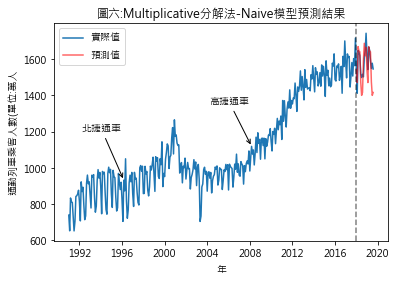
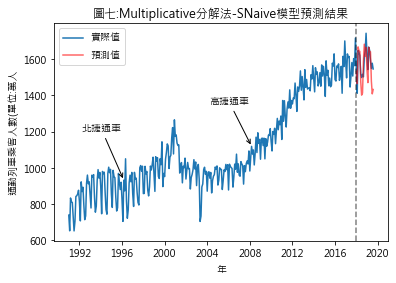
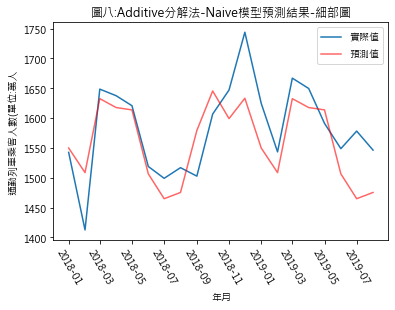
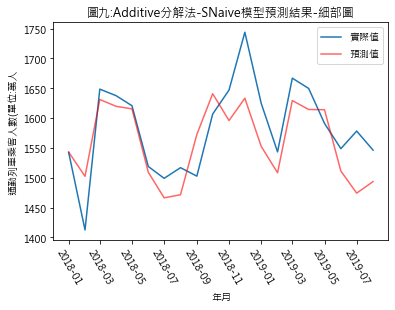
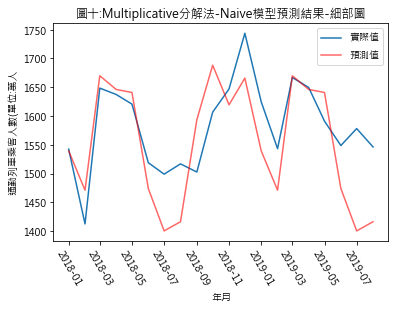
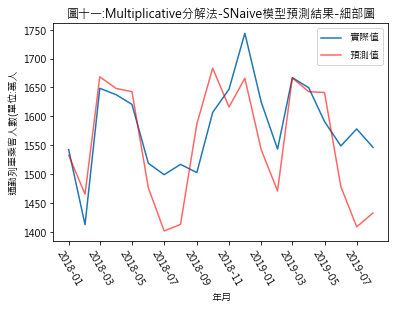
Ŷ(t+h|t) = Y(t+h-T)

Ŷ(t+h|t): t+h期時的預測值

Y(t+h-T): T期前的實際觀測值

所以若將Y設定為趨勢值,則t+h期的趨勢預測值將是

(1)additive分解法

t+h期預測值 = (t+h-T)期趨勢值實際值 + (t+h)期的季節性因素

此例t期:指2017年12月

     T:指12個月前

(2)multiplicative分解法

t+h期預測值 = (t+h-T)期趨勢值實際值 * (t+h)期的季節性因素

(三)預測結果

圖四至圖七,分別是季節性因素按additive及multiplicative方法分解後,依照Naïve及Snaïve預測方法得出的比較結果.藍線為實際數值,紅線則是依預測方法得出的2018年1月至2019年8月的預測值.圖八至圖十一則是將預測期間局部放大.用肉眼觀察,採用additive分解法的預測值似乎與實際值間的吻合度較高.但除了用目測外,還有其它方法可用來比較預測結果嗎?

(四)預測結果效能檢驗

有許多方法可用於檢驗預測效能,在此利用均方根方法(Root Mean Squared Error,RMSE),該值愈低,預測效能愈好.

1. 1.      定義:是預測與實際值二者間之差平方的期望值再求平方根
2. 2.      套件匯入

我目前沒有找到可直接算RMSE的套件,但有找到算MSE的套件,可先求出MSE的值,再算其平方根得出RMSE

(1)   MSE套件: from sklearn import metrics

(2)   平方根套件: from math import sqrt

1. 3.      語法

sqrt(metrics.mean_squared_error(實際值,預測值))

1. 4.      驗證結果

Additive分解法下的RMSE:

  1.Naïve法 :  56.594612529215105

  2.SNaïve法:  53.57873820669224

Multiplicative分解法下的RMSE:

  1.Naïve法 :  76.48135778812637

  2.SNaïve法:  73.16158281163716

從RMSE的結果來看,此例用additive分解法比multiplicativ分解法合適.

另一個有趣的結果,無論是additive法或multiplicative法,Naïve預測法求出的RMSE值都比Snaïve法略高,與直覺相符,雖然要天真活潑,但也不能天真過頭.