 
 字體:小 中 大
字體:小 中 大 |
|
|
|
| 2010/04/16 16:34:30瀏覽8849|回應7|推薦1 | |
. 商高(畢氏)定理的證明,我覺得這是一個應該要學的證明,證明的方法有很多種,維基百科都有,老師應該要教至少一個的證明,告訴學生這個定理是有原因的,而不是把這個定理當作一個口訣背起來。 . 許多人討厭數學,我是從小學就討厭數學,直到幾年前才莫名其妙又喜歡上,我回頭想想為什麼我會這麼討厭數學?或許是我問了太多課本上沒有的東西吧!老師通常會給我不是很正面的回應,甚至是情緒化的回應,後來我也懶得問了,一切都懶了,考試的成績當然也懶到趴了。 . 我記得有位生物老師,很喜歡拍投影片的機器罵人,我真怕她把投影機拍破了,有一次我學到神經細胞傳遞訊號時會分泌介質來達到工作,訊號傳遞速度會到 100m/sec ,我就問她為什麼要這麼麻煩?難道不能夠電訊號直接通過去嗎?這樣可以 300000km/sec ,結果投影機又倒楣了,真可憐;還有另一個女老師,說男生因為精囊脹脹的不舒服,所以【自慰】只是碰碰精囊把精液流出來,我嚇到了!真的嗎?真的是這樣嗎?我的精囊是這樣的嗎? . 現在年紀大了,終於明白許多老師只不過是混口飯吃罷了,會去買雞排,喜歡看好看的,喜歡人家問自己會的,甚至有時也會幹些小小的壞事,其實就只是一個普通人罷了!也就不再討厭他們了!雖然他們老是沾孔子的光!
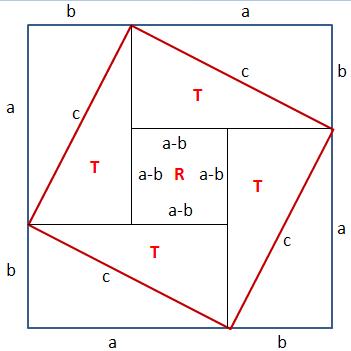
. 一個正方形內接一個邊長為 c 的正方形,從兩個正方形的交接處畫出垂直的輔助線,記住先證明出 T 是直角三角形且四個 T 是全等, R 是正方形且邊長為 (a-b) ,這裡省略證明,四個直角三角形 T 的面積和為: ......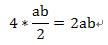 中間小正方形 R 的面積為 ...... 內接正方形面積 = 正方形 R + 四個三角形 T ...... . 直角三角形 T 的三邊長的關係也就計算出來了。 . 商高定理展示了一個極為重要的數學概念,這個概念學校沒有提,至少我那個時候沒有提,就是自然數( 1,2,3… )就只是自然數,是人類【初步】歸納出描述這個世界的方法,自然數不足以表示所有的現象,如圖的直角三角形就是一個例子: .........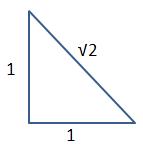 . 斜邊長根本無法用一個有限長度的數字來表達,可是它偏偏就是存在,就在你面前的三角形斜邊上,當你硬著頭皮要以自然數的數字來表達時,就會要動用科學家發明的平方逼近法等等破壞性近似的方法,就會跑出 1.414…. 無限長度的數字,換句話說永遠無法表達。 . 為什麼會有這種現象呢?就是【數字】這種現象只是整個宇宙所有現象當中的一小個,自然沒有辦法表達所有現象。 . 所以當我們計算得到根號時,是一則以喜一則以憂,喜的是有方法近似成一般數字,憂的是如果是計算到一半的時候,那將來合併的過程將是困難重重,數學轉換有一個很重要的願望,就是【 無失真轉換 】,例如我們需要丈量出 2 平方公尺正方形土地,那是不是一定要量出 1.41421356…. 的邊長才能做呢?其實只需要做出: .........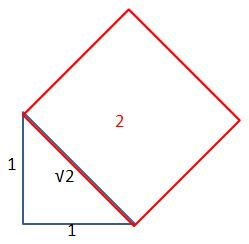 . 這個例子只是展現保持原樣 (√2) 的好處,並沒有實際的意義,根號是數學上假設的符號,是一個未開展的符號,也代表【 無失真狀態 】,順道在提到另一個無失真狀態:分數型態,分數也是無失真的符號,它比根號強的地方是它的合併非常容易,只要把分母通分即可,能化成分數型態的數叫做有理數的原因就是如此。 . 人類不斷碰到無法解決的問題,甚麼叫【無法解決】呢?其實就是走不下去,現有經驗理論無法套用,數系便從最原始的自然數,到 0 的出現,後來出現負數,負數其實也是一個不存在的東西,一路過來都是為了因應無法解決的問題而擴展了數系,後來有許多科學家開始思考一個問題: ...... . 這類的問題怎麼辦?無解!究竟這個答案是【不存在】還是只是在【數字上不存在】?我們有很多的解答並不一定要把目前問題解決才能走下一步,其實有時只要繞過去,就如同前面的根號一樣,所以尤拉發明了一個東西,好像是尤拉的發明: ...... . 【虛數的平方等於負一】,發明虛數符號還不夠,如同根號一樣,還必須定義出虛數的運算方式,因為這些刻意發明的定義與運算,能夠達到【 無失真轉換 】,所以【虛數不能分辨出大小】是不重要的,重點是【 無失真轉換 】,就算沒有辦法轉換下去,也能如同根號一樣,保留住【 無失真狀態 】, 等待下一個理論被發明出來 再行轉換,注意虛數世界的根源是 【 . 差別在哪? 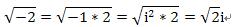 . 如上式化成屁股有 i 的符號就可以運算了,尤拉與高斯等等的偉大科學家發明出來虛數的動作方法,我們只要依照這些方式與定義動作,就可以把那個不知道是甚麼東西的東西困在 i 這個符號裡面,整個方程式動到翻掉都沒有關係,完全不受那個未知物影響,真的很厲害,能找到這樣的東西。虛數運算方式網路上都有,實數與虛數共同組成複數系,成為目前數學上的主幹。 . 轉換的發明到底有沒有用呢,很難說,那是人類的應用層面了,負數的運算建構出了【金融】,【信用交易】,買空賣空的基石就是負數運算,愛情也是負數運算,都是夢想在交互作用,【我是相信他(她)的】,問他相信甚麼東西其實也搞不清楚,越問越不能信;虛數呢?好像和原子有關吧!其實我也不懂!去問物理老師吧! . 愛情搞不好是虛數才對!那個封印是不能打開的,【你愛我嗎?愛!】,到這就好,不要再問下去了,哪裡愛?這個愛一拆開,都是慾、貪、恨、愚痴、自大、小心眼等等,會發現和原來認為的運作方式完全不搭嘎,難怪牛頓一輩子是處男!還是封印起來好了,那樣最美! |
|
| ( 心情隨筆|心情日記 ) |



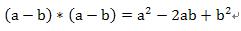
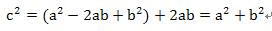

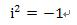
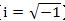 】 ,不能隨便開平方出來。
】 ,不能隨便開平方出來。 





