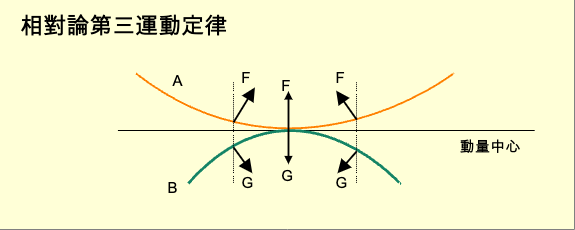
運動三定律是牛頓力學的基礎定律。在相對論中也有對應的三定律。在力學篇已經證明運動三定律來自於力學中的群體動量守恆律。而群體動量守恆律其實就是群體慣性定律。在相對論中有四維動量守恆律。而四維動量守恆律也是四維群體慣性定律。力學與相對論的差異僅在於度量。所以運動三定律如同動量守恆律也是超越度量的觀念。

在真實宇宙中，每一個物體的四維路徑都是一條線。在沒有受到外力影響的情況下，物體的線是直線。在有外力的情況線，是曲線。

曲線任何一點的彎曲程度稱為曲率。曲率的觀念是向切線對於路徑的變化率。向切線只是方向，沒有數值。一種方法是衡量方向角度的變化率為曲度。這裡採用的是由讓·弗雷德里克·弗勒內(Jean Frederic Frenet)和約瑟夫·阿爾弗雷德·塞雷(Joseph-Alfred Serret)分別提出的方法，稱為弗勒內-塞雷(Frenet-Serret)公式。

弗勒內-塞雷的方法是建構一個向量，稱為單位切向量(unit tangent vector)。向量的數值是1；方向是向切線。以這個向量對路徑微分。所得出的向量數值為曲度，方向為向法線。與這個定義適用於各種度量。

  d單位切向量/d四維路徑 = 曲率 × 單位法向量

真實四維力也是不隨觀察者或參考系變化的固定量。相對四維力是真實四維力在觀察者的座標系的四個分量所組成。

由於真實四維動量的方向就是向切線的方向，如果質量不變，真實四維力與曲率及向法線的關係是：

  真實四維力 = 質量 ×曲率 × 單位法向量

這個關係就是採用弗勒內-塞雷公式的原因。

下一步要探討相對論對應牛頓的第三運動定律：作用力與反作用力相等而方向相反。

首先要注意的是牛頓的力是三維空間的力，而相對論的力是四維力。除了在時間的分量為0，四維力是不可能方向完全相反。因此兩個四維力只能三維分量相反。

其次是牛頓的的作用力與反作用力同時發生。在相對論中沒有同時。怎麼辦？幸好除了同時之外，兩個力還屬於同一個三維空間。力學只有一個三維空間，而相對論有無數的三維空間。因此得找到既含有作用力也含有反作用力的三維空間。如何尋找呢？先從一個案例來看。

假設有A、B兩個球碰撞。兩個球的四維路徑經過碰撞自然不可能是直線。不是直線，必然受到力的作用。如何證明兩個球受到的力三維分量相等但是方向相反呢？必須A球路徑上每一個受作用力F的點在B球的路徑上都有一個對應受反作用力的點。假設A球路徑上a點受作用力F，如何找到B球路徑上對應的b點呢？幸好無論相對論或力學都有動量守恆律。在力學中可以用動量守恆律推導牛頓第三運動定律。在相對論中也可以用四維動量守恆律推導。

A球與B球可以看為一個群體，有群體動量中心。動量中心的路徑是一條直線。直線中必然有一點的垂直三維空間含有a點。這個點稱為c點。垂直三維空間必然與B球的路徑相交。交點是b點。那B球在b點所受的力G是不是就是反作用力？G的三維空間分量是不是與F的三維空間分量相等而方向相反？

依據動量中心的定義，在每一個垂直三維空間中，A的三維動量，也就是四維動量的空間分量，必須與B的三維動量互相抵消。因此在a點的三維動量與b點的三維動量互相抵消。由於碰撞，a點的三維動量與b點的三維動量都在變化。兩者的變化也必須互相抵消才能保持之後的三維動量互相抵消。然而兩者的變化率是對於動量中心的原時，不是各自的原時。原時之間依勞倫茲變換。所得的公式是：

  A勞倫茲因子^-1 F空間分量 + B勞倫茲因子^-1 G空間分量 = 0

其中四維空間的勞倫茲因子使用的不是速率，而是向切線的夾角。由於物體線是曲線，夾角不斷變化，勞倫茲因子跟著變化。公式中的勞倫茲因子是在a點和b點的勞倫茲因子。

依據動量中心的定義，兩球路徑的轉折點必然同在一個垂直三維空間。各自的四維動量與動量中心的四維路徑方向一致。勞倫茲因子為1。時間分量為0.作用力等於負作用力而方向相反。公式成為：

  F + G = 0

與牛頓第三運動定律完全一樣。

這就是相對論的運動三定律。