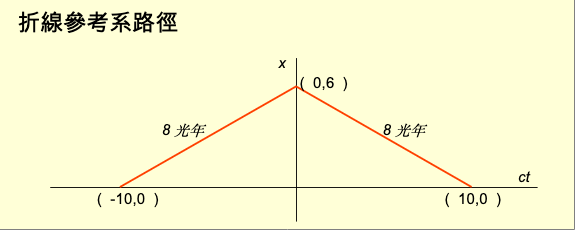
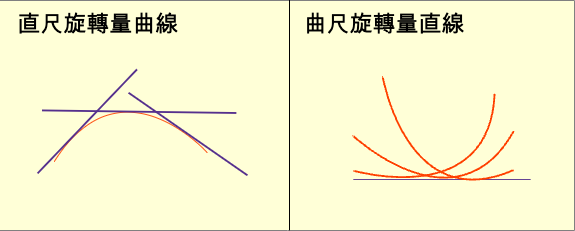
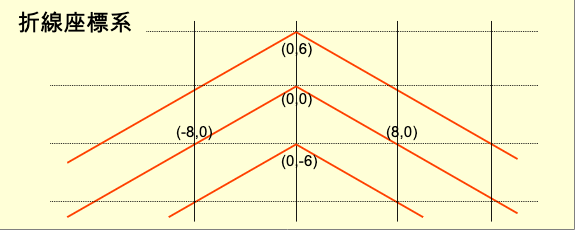
狹義相對論立足的根基是慣性參考系。主要的物理定律也都建立在慣性參考系之上。慣性參考系的四維路徑是直線。然而宇宙中的大多數物體的四維路徑都不是直線，而是曲線。以一個曲線觀察者的四維路徑作為參考系是非慣性參考系。在非慣性參考系中的時間與空間度量會是什麼呢？

在閔考斯基空間中，任何兩點之間可能的四維路徑以直線的原時最大。曲線觀察者的時間步伐較慢。在孿生子悖論中已經詳細解說過。一個孿生子甲以0.6光速到一個距離6光年的星球再返回。本來應該是花了10年到星球，返回再花10年，一共20年。但是由於時間步伐較慢，甲實際上只過了16年。而留在原地的孿生子乙過了20年。而從甲的觀點看乙，如果仍然採用閔考斯基度量，乙應該只過了9.6年。是錯的。這就表示甲的度量不可能是閔考斯基度量。

愛因斯坦相對論中的光速對於曲線參考系不再不變。光速會變意味光的路徑不再是直線，而是曲線。閔考斯基度量自然不再適用。

曲線參考系的時間度量是彎曲的。如果以直的度量器測量曲線，度量器必須旋轉，因此認為曲線是彎曲。如果以彎曲的度量器去測量直線，度量器必須旋轉。從度量器看來，直線被認為是彎曲。由於測量時間的計時器本身不能直接顯示時間步伐的變化，也就不能知道路徑是否是直線。要知道參考系是直線或曲線可以從光是否彎曲判斷。

曲線參考系的度量不是閔考斯基度量，那如何度量長度呢？物理學界通常採用的方法是微分幾何(differential geometry)中的度量張量(metric tensor)。關於度量張量留待廣義相對論再討論。這裡介紹另外一種較爲簡單易懂的方法。

第一步是建立一個座標系。在建構真實宇宙時已經說過，雖然宇宙必須能以笛卡兒座標系描述，但是不排除以其他座標系描述。既然以曲線作為參考系，座標系的ct軸就必須與曲線相重合。

如何決定三維空間的三個軸呢？慣性參考系的座標系是笛卡兒座標系。三維空間與ct軸垂直。因為是直線，所有的垂直三維空間互相平行，沒有交集。在曲線座標系在ct軸不同點的垂直三維空間會有交集，一個四維空間點會有兩個以上的座標，因此不適用。怎麼辦？最簡單的方法是採用標準座標系的xyz軸。這樣建立的三維空間仍然互相平行，沒有交集。

如何使用這個曲線座標系度量長度呢？這個曲線座標系與標準座標系之間存在雙射關係，因此每一個點的座標都對應一個標準座標。任何一條線都既可以被曲線座標系也可以被標準座標系描述。將曲線座標系的描述變換成標準座標系對應的描述，就可以用閔考斯基度量計算長度。

這裡以孿生子悖論中的折線路徑為例演示非慣性參考系的時空度量計算。

折線參考系由在ct-x平面與標準參考系ct軸夾角30.96度的直線抵達(0,6,0,0)位置。然後順時針旋轉118.08度延伸出去。這條折線是折線座標系的ct軸。轉折點是原點。xyz軸與標準座標系方向一致。長度單位是光年。

折線座標系的ct軸上的度量是參考系本身路徑的長度。譬如從轉折點到與標準座標系ct軸的交點長度是8光年。依據這個觀念，折線座標系位置(0,0,0,0)對應標準座標系(0,6,0,0)。位置(-8,0,0,0)對應標準座標系(-10,0,0,0)。位置(8,0,0,0)對應標準座標系(10,0,0,0)。

折線座標系任何一點(ct,x,y,z)對應標準座標系(⁠ct́,x́,ý,ź)的映射公式是：

ct<0 ct́=1.25ct, x́=x+0.75ct+6, ý=y, ź=z
ct>=0 ct́=1.25ct, x́=x-0.75ct+6, ý=y, ź=z

由於任何一個慣性座標系的度量都是閔考斯基度量，上述折線座標系並不必須映射到標準座標系，映射到任何一個慣性座標系都可以恢復閔考斯基度量。

從這個例子可以看出，任何一條曲線參考系都可以用同樣的方式建構座標系，以及對應慣性座標系的映射函數。

從上面的討論可以看出，度量與座標系相關。物理上笛卡兒座標系可以支持閔考斯基度量，也可以支持歐幾米得度量。曲線座標系卻不能支持其中任何一種，但是卻可以對應笛卡兒座標系。關於座標系與度量的關係留待以後深入探討。