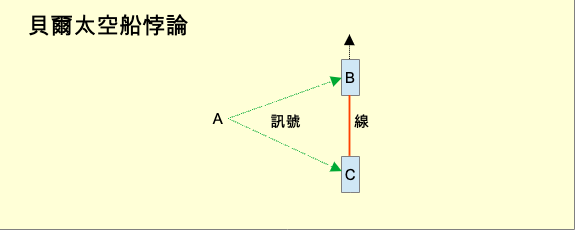
貝爾太空船悖論原先是德灣(E. Dewan)與貝然(M. Beran)在1959年提出。經過約翰·貝爾在1976年略為修改後重新敘述而以貝爾太空船悖論聞名。

根據維基百科的敘述，貝爾太空船悖論如下：

有三艘太空船A、B、C。一開始都與同一個慣性參考系相對靜止。AB之間的距離與AC之間的距離相等。B和C船頭指向同一個方向。B在前，C在後。B船尾和C船頭之間連著一條纖弱的線。B和C都存有相同關於何時加速多少的指令。然後從A送一個訊號同時抵達B和C。收到訊號後，B和C同時啟動。依照指令加速。A本身維持不動。貝爾認為：「對A來說，在任何時間B和C的速度完全相同。B和C的距離永遠保持不變。」隨著B和C加速，線會不會斷？

這個問題引起很多爭論。一般來說有三種意見：

• 雖然有加速，B和C的距離不變，因此線不會斷。
• 加速會導致長度收縮，因此線會斷。
• 加速會施力於線，因此線會斷。

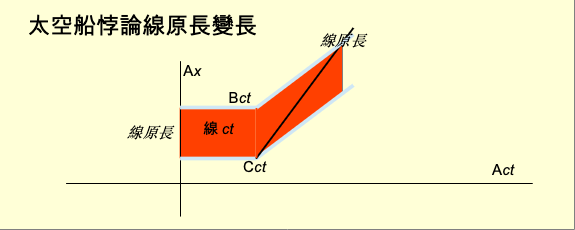
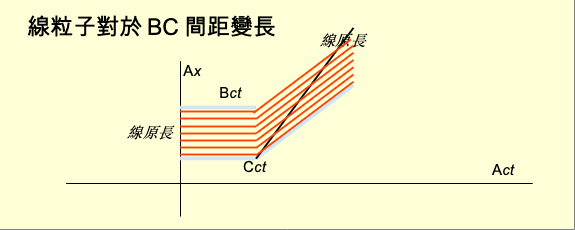
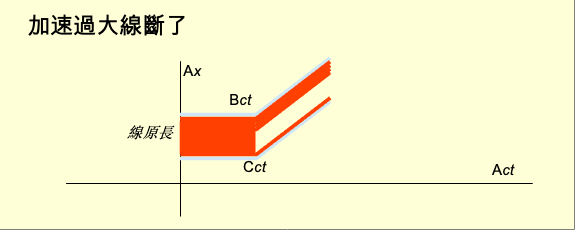
究竟哪一個對呢？

首先要澄清，整個悖論的先決條件是：「對A來說，B和C的距離永遠保持不變。」之前的敘述只是為了達成這個條件。A四維路徑每一個位置都有一個垂直三維空間。每一個三維空間都有B和C的切體。距離指的是每一個空間中兩個切體的距離都相等。

先考慮長度收縮會造成線斷的論述。B和C的加速導致兩者的四維路徑是曲線。雖然從A看來兩者之間的距離不變，也就是線的長度不變。但這不是線的原長，而是收縮後的長度。線的原長是線本身的垂直三維空間中線的長度。線的原長變長了。原長才是線的真正長度。當原長變長會對線產生張力(tension)。張力達到一定程度就會將線拉斷。

反對以上論述者的理由是線要斷掉需要張力。長度收縮來自勞倫茲變換。勞倫茲變換只是觀察者之間的變換，不會產生張力。因此不會斷。

認為線會斷的另一個理由是線綁在火箭上，火箭加速會連帶線跟著加速。線要加速必然被施力。纖弱的線受了力而斷開。所以線會斷，但是原因來自加速。

那麼應該如何看這個悖論呢？

首先這個悖論的敘述不夠清晰，其中有兩個觀念需要澄清。第一個需要澄清的是判斷線斷的標準。一般將線拉斷的方法是以兩手握住線的兩端，向兩邊拉扯。線從中間斷開，分成兩段。判斷的標準可以有兩種。一種是將兩段之間的引力低於某值F，以至於一段運動不會影響到另一段，判為斷開。另一種是將兩段之間的空間距離超過某值L判為斷開。空間距離越遠引力越小。所以兩個判斷方式基本一致。

線由粒子組成。粒子連接在一起成為線段。所以在線段中任何兩個粒子必然存在至少一個由粒子組成的連接鍊。鍊中每一顆粒子與相鄰的粒子距離小於L。線段中的任何一顆粒子與另一段的任何一顆粒子的距離必然大於L。

依據這個定義可以出現兩種情況。一種是線段中有許多粒子。另一種是線段只有一個粒子。如果整條線的每一個線段都只有很少的粒子，線不只是斷了，而且粉碎了。

假設線的每一顆粒子會自己加速，與B和C同步。對A來說，任何兩個粒子之間距離不變。那麼從A看來，線沒有斷。然而從B或C看來，在它們的垂直三維空間們中，粒子之間的距離在增加，直到距離大於L。對於B或C來說，線粉碎了。所以在這種情況下，線斷與否相對於觀察者。而加速的作用僅僅是B或C的方向上的改變導致垂直三維空間的改變，並沒有其他作用。線雖然碎了，但是仍然與B和C同步加速，並沒有散。

在悖論的敘述中線的粒子本身沒有加速能力，而是被B拖著加速前進。因此會被B施力。這就得澄清纖弱的意思。纖弱可以定義成只能承受很小的力F就會斷。這個觀念與力學一致。差別是力學的力是三維空間的三維力。相對論是閔考斯基空間的四維力。

當B加速很慢，線所承受的力小於F，線不會斷。當B加速很快，快到施於線的力大於F，線就斷了。線斷了以後，與B連接的一段會拉直，隨B的加速前進。與C連接的一段會落至C的頂端，被C推著前進。

綜合以上兩種情況，對於悖論的解答是如果B加速產生的力大到線不能承受，無論A、B、C都會認為線斷了。如果B加速很慢，但是持續加速，A不會認為線斷了，但是最終B和C會認為線粉碎了。

這個悖論很清楚的展現愛因斯坦相對論與真實相對論觀念上的差異。愛因斯坦相對論的物體是三維物體。愛因斯坦相對論對於原長(proper length)的理解是物體原本的長度。爭議點在對於原長增加的理解。認為原長是物體是實際長度的人因為原長增加，認為線會斷。認為原長增加僅僅是勞倫茲變換的結果，認為線不會斷。

真實相對論認為物體是四維物體。物體四維形狀固定，不會因為觀察者變化。人類看到的物體是觀察者垂直三維空間對物體的切體。原長僅僅是物體本身四維路徑的垂直三維空間對物體切體後所得到的長度，與其他觀察者看到的長度沒有更多的意義。也就是說根本沒有實際長度。所以不存在爭議。