字體:小 中 大
字體:小 中 大 |
|
|
|
| 2025/08/15 03:40:42瀏覽56|回應0|推薦0 | |
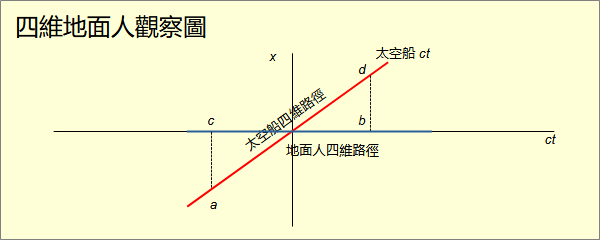
相對論從提出到現在已經超過100年。當愛因斯坦提出狹義相對論時物理界對時空的理解尚停留在力學的會隨時間變化的三維空間的觀念上。以至於除了閔考斯基,其他的物理學者對於相對論中推導出的許多現象的理解是錯的。這些錯誤流傳到今天仍然在書籍裡、課堂中繼續誤導學生。在前面幾篇已經破除了長度收縮、同時的觀念。這一篇破除時間膨脹(time dilation)的觀念。 一般對於時間膨脹的敘述是這樣的: 地面上有一個人看到天上有一艘太空船以高速在天空中通過。太空船向地面發射一束光。光反射回太空船。地面上的人看到光斜射到地面再斜反射回太空船。所花的時間是 這樣的敘述在相對論中很常見,卻不嚴謹。狹義相對論的光速不變有一個前提,就是觀察者必須是慣性參考系。這意味著在四維空間中,觀察者的四維路徑必須是直線。直線必然與真實方向的夾角不變。也就是說在相對論中,慣性參考系的慣性必然是真實慣性。至於相對慣性。相對論沒有相對慣性。在力學篇之前對於力學的真實慣性與相對慣性有詳細解說。可以與相對論相比較。 時間膨脹也有悖論。 地面上的人也向上射一束光。在太空船經過時剛好射中太空船反射向地面。所花的時間是地面時間 = 太空船高度/光速 。而太空船上的人看到光光斜射到太空船再斜反射回到地面。所花的時間是 地面的時間怎麼可以既比太空船時間慢又比太空船時間快?這是時間膨脹悖論。 要解開時間膨脹悖論前先要理解時間膨脹現象。 真實相對論的物理架構是:「四維真實宇宙經過人類慣性觀察者測量而成為閔考斯基空間。發生在閔考斯基空間的現象是四維現象。人類慣性觀察者觀察四維現象而得到三維現象。」所以要理解相對論的三維現象得逆向回推到閔考斯基空間的四維現象。 時間膨脹的四維現象是什麼? 時間在相對論是度量。1秒=1光秒。物體是四維超體。由於時空度量規模的巨大差異,所有的四維超體都是極細的線。線是物體的四維路徑。沿著四維路徑以計時器測量的長度是物體的原時。四維路徑上一點是物體的一個時刻。人類觀察者也是物體。人類在任何一個時刻觀察到的物體是在該時刻垂直三維空間與物體的切體。 地面的人在a點看到太空船在四維空間的c點。之後在b點看到太空船在四維空間的d點。a點與b點是在人的四維路徑上。a點與b點的距離,也就是時間差,是沿著人類四維路徑兩點之間的長度。c點與d點在太空船的四維路徑上。c點與d點的距離,也就是時間差,是沿著太空船四維路徑兩點之間的長度。這就是太空船的時間與地面時間不同的原因。路徑都不同,哪有什麼時間膨脹。 時間膨脹的悖論又是什麼? 太空船上的人看物體是看到的是物體被自己的垂直三維空間切割地切體。c點的垂直三維空間切割地面人四維路徑的點不是a點;d點的垂直三維空間切割地面人四維路徑的點不是b點。點都不同,哪有什麼悖論。 以上的論述可以用實際的數字演示。為了講解方便,將敘述中地面的人移到太空船的高度。其餘不變。落實所有的度量。高度為1光秒。太空船對地面速度為0.6光速。太空船在與人相遇時射出光線。 建立一個笛卡兒座標系。以地面上的人的四維路徑為ct軸。x軸的方向是太空船行駛的方向。y軸方向是太空船向地面的方向。太空船的四維路徑是向x軸傾斜31度的斜線。tan(31)=0.6。太空船發射光線也就是c點的位置座標為(0,0)。這也是人的a點位置。太空船收到反射光也就是d點的位置為(2.5,1.5)。線段長度為2光秒。人的b點位置是(2.5,0)。a點與b點的距離是2.5光秒。c點與d點的距離是2光秒。 時間膨脹現象在三維歐幾米得空間有對應的現象。 在地上放一把尺A。斜放另一把尺B一端在A上,方向與A夾角36.8度。一個人從交點沿著A前進。到達2公尺的位置。橫看B尺的標示是2.5公尺。然而沒有人會認為這是長度縮減。 |
|
| ( 知識學習|科學百科 ) |


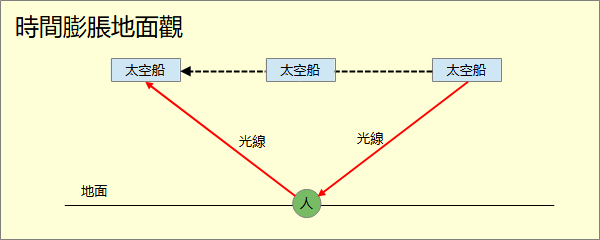
 。而在太空船上的人看到的是光線直射到地面再直反射回太空船。所花的時間是太空船時間 = 太空船高度/光速。太空船時間過的比地面時間緩慢。這個現象稱為時間膨脹。
。而在太空船上的人看到的是光線直射到地面再直反射回太空船。所花的時間是太空船時間 = 太空船高度/光速。太空船時間過的比地面時間緩慢。這個現象稱為時間膨脹。
 。地面時間過的比太空船時間緩慢。
。地面時間過的比太空船時間緩慢。