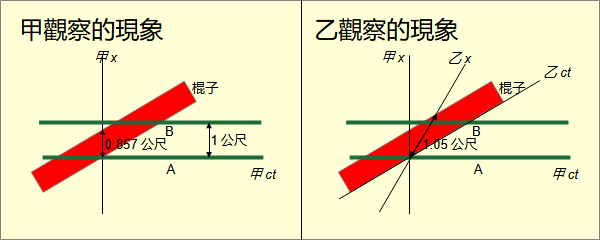
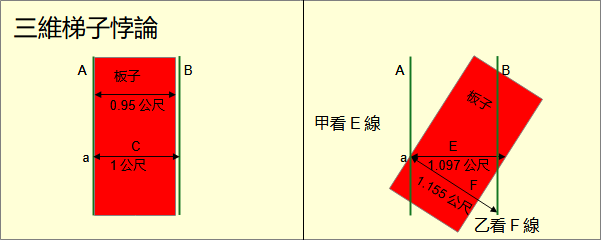
在二十世紀初，愛因斯坦剛提出相對論不久，物理界仍然對相對論將信將疑，仍然以傳統力學的時空觀念看待相對論，遂產生了許多所謂的悖論。其實這些所謂的悖論只是出於對相對論的誤解，並不是真正的悖論。其中就有梯子悖論(ladder paradox)，也稱為竿與穀倉悖論(barn-pole paradox)。

這個悖論依據維基百科的敘述：

有一個梯子和一個有前門與後門的穀倉。梯子的長度比穀倉前、後門間的靜止長度要長。如果梯子不移動的話，其是無法容納進整個穀倉裡的。

此時如果有一個人，拿著這個梯子，以接近光速的速度，向穀倉運動的話。對於站在穀倉，一名靜止旁觀者而言，因為收縮效應，當梯子高速移動經過穀倉時，可以完美地容納進穀倉。也就是說，對於這名旁觀者而言，梯子的長度小於穀倉前、後門間的長度。

但是另一方面，對於拿著梯子的人而言，由於與梯子沒有相對速度，因此梯子並不會縮短。反而是觀察到穀倉以接近光速的速度向自己移動，因為收縮效應，穀倉會收縮。也就是說，對於拿著梯子的人而言，梯子的長度大於穀倉前、後門間的長度。

梯子怎麼可能又長於穀倉，同時又短於穀倉？

梯子悖論是一個偽悖論。維基百科的解釋是在相對論中對於每位觀察者｢同時性｣是相對的。這個解釋是錯的。相對與同時的意義互相矛盾。同時就不可能相對，相對就不可能同時。在相對論出現的初期，物理學界仍然以力學的三維空間看待相對論。將許多舊的觀念錯誤地直接沿用到相對論。相對論根本沒有｢同時｣這個觀念。也就是說，現象可以存在，但是問題錯了。那應該怎麼理解這個現象呢？

這個悖論是以時間為參數的三維空間敘述。而相對論的宇宙是四維的閔考斯基空間。要理解這個悖論得改換成以閔考斯基空間敘述。

這個悖論的敘述即使在三維空間也過於複雜，再換成四維空間之前，先簡化到最基本的三維論述。

地上相距1公尺畫A、B兩個點。一條直線連接兩點。一根極細長1.05公尺的棍子。將棍子沿著直線以0.577光速移動。地上靜止的觀察者甲在某一個時刻看到棍子夾在兩點之間。而隨棍移動的觀察者乙從沒有看到這一現象。

再以四維重新敘述一遍。

在真實宇宙中並不分時間、空間，而是渾然一體。是人類以計時器測量時間，以尺測量空間而分成時間與空間。每一個人，推及到每一個物體，以自己為參考系測量時間與空間，因此有自己的時間與空間。由於光與真實方向在任何一點的夾角都是45度，加上測量方法相同，每一個人測量出的時空度量都是閔考斯基度量。同在地球上的人，測量的時間雖然不同，但是差異極小。

物體在四維空間是四維超體，有時、長、寬、高四維長度。由於1秒等於1光秒的長度，任何物體都是細長的一條線。這條線是物體的四維路徑。路徑的長度是物體的原時。

物體在任何一個時刻都有一個垂直於四維路徑的三維空間。物體在自己的垂直三維空間的切體的長、寬、高是物體在該時刻的原長、原寬、原高。

人類觀察者本身也是四維超體。人在一時刻觀察到的三維形體是物體在人的垂直三維空間的切體。當物體的四維路徑與人的四維路徑的夾角等於0度，人的垂直三維空間與物體的垂直三維空間完全重合。人看到物體的度量是物體的原長、原寬、原高。

當物體的四維路徑與人的四維路徑的夾角不等於0度，人觀察到物體在移動。速度是tan(夾角)。人的垂直三維空間與物體的垂直三維空間不一樣。人看到物體的度量是物體的斜長、斜寬、斜高。

為了敘述方便，建一個ct-x的座標系。地上A、B兩點成為與ct軸平行，沿x軸相距1公尺的A、B兩條線。棍子成為與ct軸平行，沿x軸長度1.05公尺板子。將板子向x軸旋轉。超過某一個角度後與ct軸平行的觀察者甲看到在某一時刻板子的三維切體，也就是棍子，落在兩點之間。而與板子平行的觀察者乙在任何時刻都只看到棍子至少有一段落在兩點之外。

在｢長度其實沒有收縮」中已經說明，所謂長度收縮其實只是在閔考斯基空間中斜長小於原長的現象。斜度越大，棍子對於甲的斜長越小。當夾角到30度，板子斜長是0.857公尺，自然能落在兩線之間。在乙的任何時刻，三維空間都與板子的三維空間重合。看到的是板子的原長。當然至少有一段落在兩點之外。

所以梯子悖論現象的根本原因是兩個觀察者由於四維位置與方向不同，測量的是兩條不同的線段。

其實在三維歐幾米得空間有對應這個悖論的現象。

在地上畫A、B兩條極長相距1公尺的平行線。A線在左，B線在右。一塊極長寬0.95公尺的板子。將板子左邊沿A線放入兩條線之間。板子可以完全放入。任何觀察者沿著任何橫過板子的線看到的都是板子在兩線之間。

在A線任選一點a畫一條垂直線C到B線。C線長1公尺。在板子靠a點劃一條垂直線D直到右邊。D線長0.95公尺。D線與C線重疊。

在板子靠a點順時針方向旋轉30度。在板子左邊靠a點沿著C線畫一條直線E到板子另一邊。E線的長度是1.097公尺。一個沿著E線的觀察者甲看到板子突出B線。

從A線的a點沿著D線畫一條直線F到B線。F線的長度是1.155公尺。沿著F線的觀察者乙看到板子仍然在兩線之間。

板子的寬度怎麼可能同時既大於兩線之間的距離，又小於兩線的距離？

在隨時間變化的三維空間中可是有｢同時｣的，但是無助於回答這個問題。實際上沒有人會認為這是悖論。E線與F線，根本是兩條不同的線。自然長度不同。

梯子悖論雖然是偽悖論，理解其現象的根源還是有助於理解相對論。