

 字體:小 中 大
字體:小 中 大 |
|
|
|
| 2025/07/02 00:10:53瀏覽27|回應0|推薦0 | |
在我學狹義相對論時,總有一個疑問縈繞心頭。為什麼宇宙的度量是閔考斯基度量?愛因斯坦說是因為光速不變。那為什麼光速不變?閔考斯基說是因為閔考斯基度量。總是在兜圈子。會有這個問題是因為閔考斯基度量感覺上怪怪的。總覺得哪裡不對。宇宙不應該是這樣的。直到我認知到真實物理與景象物理的區別才知道這根本不是宇宙的本質,而是人類觀察所賦予的性質。 有了這樣的認知,思路逐漸清晰。光速不變是人類觀察的結果。速度是長度除以時間。那麼如果長度與時間隨觀察者一起改變,光速就能保持不變。因此光速不變不是原因,而是結果。同樣的閔考斯基度量不是原因,而是結果。要徹底理解原因,就得找出光在人類觀察前的真實行為,以及人類如何觀察導致光的路徑長度與時間一起改變。 首先考慮時間是怎麼一回事。人類測量時間需要計時器。愛因斯坦在相對論中採用光鐘當計時器。光鐘是兩面平行相對的鏡子。光在兩面鏡子間來回反射。以反射的次數計算時間。因此癥結在於光的行為。 光的行為本身並不受人類觀察的影響。光在人類觀察前的規律是什麼呢?經過深入的研究,最終建立的真實論已經在前篇敘述。其中的描述規律是真實物理的定律。這篇敘述如何從真實論經過人類觀察得出狹義相對論。 真實論說宇宙有真實方向。假設有一個人類觀察者甲。甲的線段方向與真實方向一致。或者說甲的路徑沿著真實方向前進。就以甲的路徑為參考系。方向從過去指向未來。沿真實方向的參考系稱為標準參考系。 真實論說有一個四維笛卡兒座標系使得真實方向是一條直線。將座標系的四個軸設定為(ct,x,y,z)。座標系的單位是光秒。讓ct軸與參考系重合。ct軸的正向與參考系的方向一致。穿過ct軸任何一點的光線會與ct軸夾角45度。光速,也就是時空單位轉換常數是1光秒/秒。這樣的座標系稱為標準座標系。
計時器採用愛因斯坦的光鐘。將鏡子一面鏡子A放置在甲身上,面對y方向。另一面鏡子B放置在y方向距離甲1光秒的位置,面對甲。A的路徑與甲重合。B的路徑與甲距離1光秒。 將計時開始點設為原點。光從A射向B。當光到達B時,甲的原時(proper time)經過1秒。當光從B反射到達A時,經過2秒。到達點座標為(2,0,0,0)。就這樣來回反射,甲的原時以2秒為單位增加。
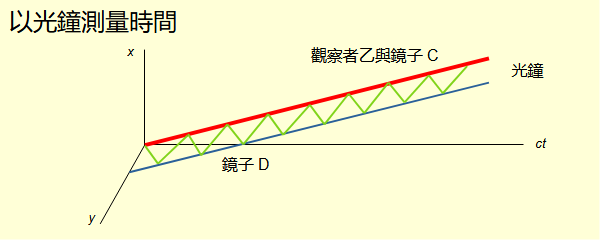
假設有另外一位觀察者乙。路徑也是直線。通過座標原點。從ct軸向x軸方向傾斜θ度。θ必須小於45度。以三維空間理解,相對於參考系,乙以tan(θ)光速向x軸方向前進。假如θ是30度,乙的速度是 乙也用光鐘測量時間。光鐘的鏡子C放在乙身上,面對y方向。另一面鏡子D放置在y方向距離乙1光秒的位置,面對乙。C的路徑與乙重合。D的路徑與乙距離1光秒。 將原點設為計時開始點。光從C射向D。當光到達D時,乙的原時經過1秒。當光從D反射到達C時,經過2秒。問題是,到達C點的座標是什麼? 依據真實論,無論鏡子怎麼放,光行進的路徑仍然必須與真實方向夾角45度。因此到達C點的座標是 由於θ可以是任何大於0度,小於45度的角度,從以上討論可以得到對於原點2光秒,沿x軸的對原點2光秒的等距線4 = ct2 - (x2+y2+z2)其中y與z均是0。如果只看(ct,x)平面,是一條雙曲線。傾斜方向可以是任何方向。對原點2光秒的等距體為4 = ct2 - (x2+y2+z2)。調整光鐘兩面鏡子距離可以得到對原點任何距離的等距體s2 = ct2 - (x2+y2+z2)。s是對原點的距離。由於原點可以是任何點,公式變成對於任何兩點(ct1,x1,y1,z1)與(ct2,x2,y2,z2)之間的距離s2 = (ct2-ct1)2 - ((x2-x1)2+(y2-y1)2+(z2-z1)2)。s是兩點之間的四維距離,也是聯繫兩點直線段的原時。 如果要計算曲線長度得採用微積分表述。公式變成微分ds2 = dct2 - (dx2+dy2+dz2)。這就是閔考斯基度量公式。 由於四維距離是由光鐘測量出的原時,不會因參考系或座標系改變,所以適用於任何參考系與座標系。 至此新的物理架構已經完整呈現。新物理架構是真實物理經過人類觀察產生景象物理。真實物理有自己的真實物理觀念以及物理定律。現在物理學界的物理是景象物理。以新的物理架構對物理的理解會更清晰,更容易融會貫通。。 |
|
| ( 知識學習|科學百科 ) |



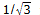 光速。
光速。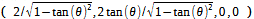 。
。





