狹義相對論有兩種切入點。一種是愛因斯坦的光速不變原則。另一種是閔考斯基的四維閔考斯基空間。閔考斯基空間是一個度量為閔考斯基度量的四維空間。再依據閔考斯基度量推導出光速不變。推導順序是從基礎觀念推導出結果。是順向推導。較容易理解。而愛因斯坦從光速不變推導出閔考斯基度量，是從現象推導基礎觀念。是逆向推導。較難理解。因此出現了許多悖論。這些悖論以閔考斯基空間理解，其實很簡單。

閔考斯基度量的定義是在閔考斯基空間中的任何兩點的平方距離是:
兩點四維距離² = (兩點時間距離 × 光速)² - 兩點三維空間距離²

在相對論中有兩種空間。第一種空間是宇宙的四維空間。另一種是符合人類直觀的三維空間。閔考斯基度量中的空間指的是三維空間，是四維空間的次空間(subspace)。兩個名稱一樣，涵義完全不同。所以凡提到空間必得指明是四維空間還是三維空間。同樣的情況也發生在距離上。在相對論中必須明確指出是三維距離還是四維距離。物體在一點的速度則是三維空間距離對於時間距離的變化率。

光速在愛因斯坦相對論中指的是光的速度。在閔考斯基度量中的意義卻是時間長度與三維空間長度的轉換常數。假設兩點時間距離是1秒。乘以光速後是1光秒。等於299,729,458公尺。在四維空間中所有的點在本質上並沒有差異。那麼以計時器測量的時間長度與以尺測量的三維空間長度本質上沒有什麼不同。因此1秒本質上就是1光秒，根本必轉換。上面的閔考斯基度量公式可以改寫成
兩點四維距離² = 兩點時間距離² - 兩點三維空間距離²

一個人身高不過兩公尺，而一秒就有近3百萬公尺。一個人的四維超體的形狀是一條極細的線。任何一個人觀察到的物體，其四維超體也是一條極細的線。就連地球、太陽這些看來巨大的星球也不例外。這個時空單位的巨大差異就是電子計算機能計算那麼快的根源。

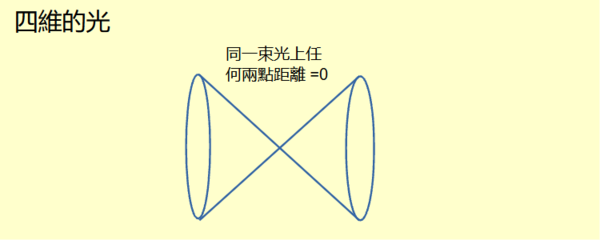
閔考斯基度量公式中的四維平方距離是時間平方距離減去三維空間平方距離。當兩者相等，兩點四維距離為0。當距離等於0，將三維空間距離除以時間距離得到的是光速。所以光所經過的途徑上任何兩點的四維距離為0。

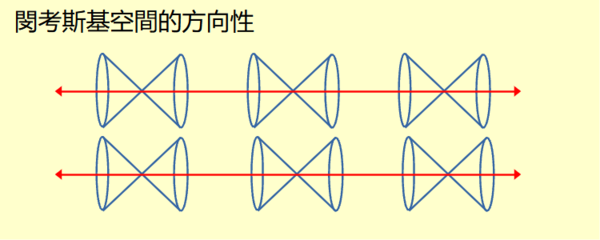
由於所有的光的速率都是光速。任何兩束光最多只能相交一點。所有通過一點的光形成一個三維正錐面。每一個三維正錐面都可以有一條中心線通過。任何兩條中心線只能平行或重合。據此證明閔考斯基空間具有方向性。方向是中心線的方向。這個方向是真實論的觀念，稱為真實方向。狹義相對論是建立在具有真實方向的四維空間上。這個方向對於貫通閔考斯基空間至關重要。

雖然宇宙方向性的推導是建立在閔考斯基空間上，力學的宇宙以及廣義相對論的宇宙都具有方向性。力學的宇宙時間維度與三維空間互相獨立。時間維度的方向就是力學宇宙的方向。廣義相對論宇宙方向性後續會討論。

閔考斯基度量有一個嚴重的問題。四維距離是由時間距離與三維空間距離所構成。然而度量公式卻沒有提供任何資訊來決定兩點之間的時間距離與空間距離。舉例來說，一個四維超體是一條極細的直線。在前一篇已經說明，線的長度是可以由計時器測量，是時間的長度。所以在這個超體上的任何兩點只有時間距離。這個論述卻沒有辦法從閔考斯基度量公式直接推導。有了真實方向，這個問題就有了答案。

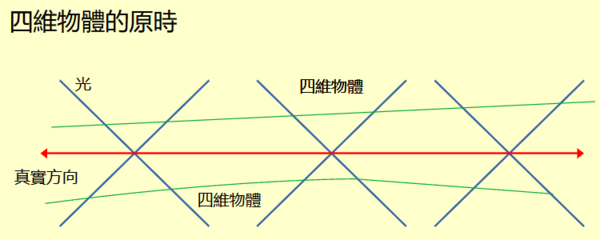
四維距離是連結兩點之間直線線段的長度。當直線與真實方向的夾角小於45度，直線線段的長度是線段的原時。進一步推論。如果一條線段，不必是直線，中每一點的切線與真實方向的夾角都小於45度，線段的長度是線段的原時。

那三維空間度量是不是與真實方向夾角超過45度的線段呢？不盡然。後續會詳細說明。