在前面幾篇已經說明，狹義相對論的宇宙是閔考斯基空間。閔考斯基空間是度量為閔考斯基度量的四維空間。閔考斯基度量由時間度量與三維空間度量組成。宇宙有方向性。方向是真實方向。宇宙中與真實方向夾角小於45度的線段長度只有時間度量，是線段的原時。具有原時的線段稱為原時線段。其他大於45度的線段呢？

想像一個長方體的箱子。箱子本身是四維超體。除了原時外還有長、寬、高三個三維空間度量。這三個度量怎麼來的？

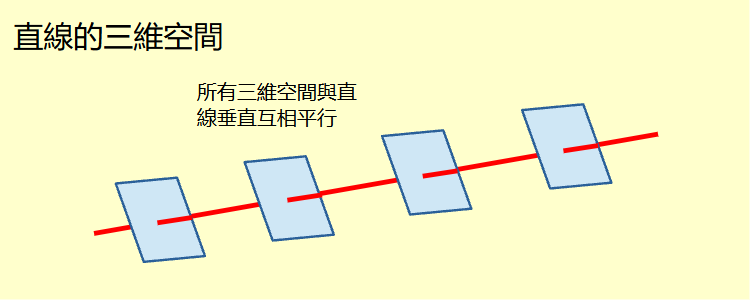
這個問題先從數學考慮。想像一個四維的歐幾米得空間。空間中任意取一條直線。直線上任意取一個點。與直線垂直通過這個點的所有的直線集合成一個三維空間。這個三維空間依附在直線的這個點上。直線上每一個點都依附著一個這樣的三維空間。直線上每一個點依附的三維空間互相平行不相交。

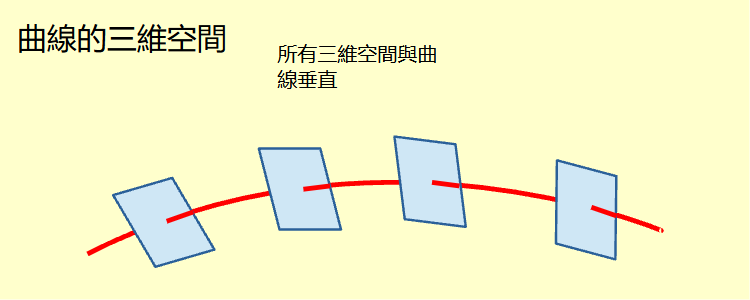
將直線改成曲線。曲線上每一個點都有一條切線通過。與切線垂直通過這個點的所有直線也集合成一個三維空間。曲線上不同點所依附的三維空間不一定平行，可能相交。

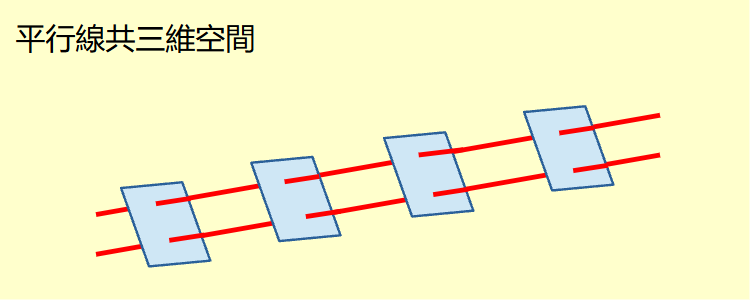
當兩條線平行時，兩條線上對應點的三維空間完全相同。

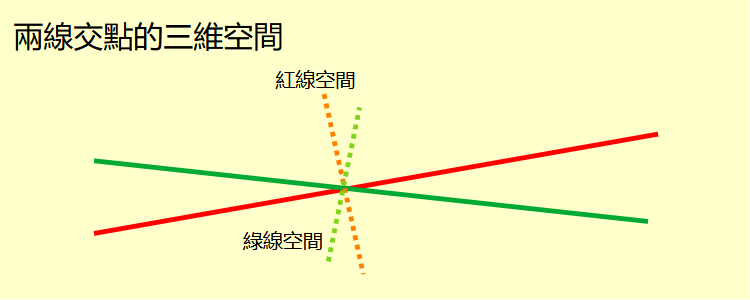
很顯然的這樣產生的三維空間由線與線上的點共同決定。設想有甲乙兩條線在A點相交。甲線在A點的切線方向與乙線在A點的方向不同，因此甲線在A點的三維空間與乙線在A點的三維空間不同，但是都含有A點。

將四維空間的度量改成閔考斯基度量。空間成為閔考斯基空間。所有上述基於歐幾里得空間的論述不必改變仍然成立。

到目前為止，所有的論述都是數學。下一步是賦予物理意義。又得回到真實方向與原時線段。所有物體的四維超體的線段都是原時線段。在狹義相對論中，只有原時線段上的點才有依附的三維空間。任何在三維空間中的線段只有三維空間度量，沒有時間度量。

回到前面提到的箱子。四維箱子與自己原時線段上的任何一點所依附的三維空間相交，必然形成一個三維箱子。這個三維箱子有三條線段長度是箱子的長、寬、高。這三條線段都在三維空間中，只有三維空間度量。

無論三維空間度量值或時間度量值，在閔考斯基空間中都以閔考斯基度量合成一個四維度量值。閔考斯基度量公式
  兩點四維距離² = 兩點時間距離² - 兩點三維空間距離²
如果箱子長度是1公尺。時間距離為0。三維空間距離為1公尺。四維長度平方是-1平方公尺。長度是1i公尺，是虛數。虛數是什麼意義？後續再討論。

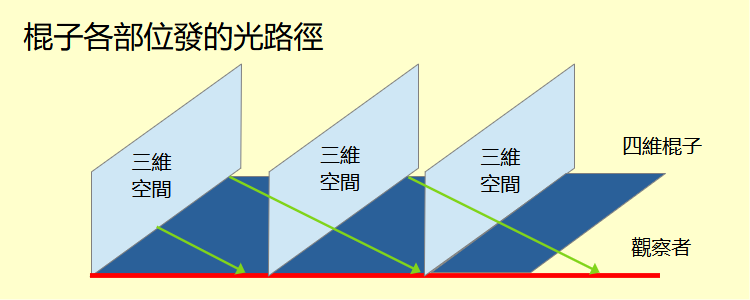
原時線段的三維空間是物理學刻意設定的。觀察者看到的三維物體並不是四維超體與三維空間的交集。想像一根有1根很長的棍子。一端緊貼著觀察者。另一端距離觀察者有1光秒。觀察者看到的是棍子的光到達眼睛的影像。棍子近端的光花0秒到達，是現在的三維空間中的棍子。棍子遠端的光需要1秒才到達，是1秒前的三維空間中的棍子。也就是說，整個棍子的影像是由不同的三維空間中棍子各部位組成。

想像棍子就是一把有刻度的尺。遠端刻度減去近端刻度是棍子的長度。假設棍子的遠端在這1秒間忽然消失，觀察者不可能觀察到。那麼算出的長度是1秒前的長度。如果近端也在這1秒間消失。那麼算出的長度既不是1秒前三維空間也不是現在三維空間的長度。

棍子在光線發出後可能發生變化而導致誤判。那麼觀察不是沒用了​？這就顯出時間度量1光秒等於299,729,458公尺的重要性。在人類生活的環境中時間度量遠大於空間度量。一個最遠離觀察者100公尺的物體，光線傳到人的時間僅33奈秒。物體幾乎不可能在這個時間中有任何改變。人類才可能依據直接觀察推導出物理規律。傳統物理學得以發展。

相對論處理的空間規模堪比時間。不能忽視光到達觀察者的延遲。相對論中有一些悖論就牽涉到觀察到的物體與現在的三維空間的差異。後續會一一解說。