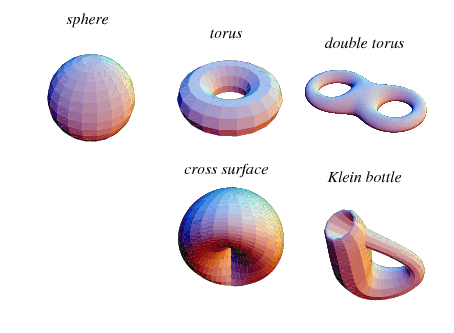從﹝弦論 O﹞到﹝弦論六﹞這一路下來，我們瞭解到，愛因斯坦的廣義相對論把重力物理與時空幾何連結起來，而弦論更強化並深化了物理與幾何之間的關聯性。接下來讓我們看看近二十年來物理學家們獲得怎樣的最新進展。

1988 年，史丹佛的蘭斯‧迪克森，歐州核研組織﹝CERN﹞的伍爾夫庚‧勒奇，哈佛的瓦法，和麻省理工的尼克勞斯‧華納，以基於對稱美學方面的理由，倡議當兩個不同的卡拉比‧丘流形，被選擇用來做為弦論裡那些蜷曲起來的多餘維度的時候，有可能造成兩個物理性質完全相同的宇宙。

這裡有點難懂。講明的話是這樣的：弦論不是說空間有十度嗎？這十度裡有三度是不蜷曲、舒展開來的，即為我們所熟知的長、寬、高這三個維度。其餘七個度我們說，捲起來，看不見了。整個宇宙的空間裡每一個點，都存在著這七個空間度蜷曲起來，無法觀測的「球」，叫「卡拉比‧丘流形」或「卡拉比‧丘空間」。

如果我們知道這七個空間度是怎麼個捲法，不就完全瞭解宇宙的時空真面目了嗎？問題是，在無以數計可能的眾諸卡拉比‧丘流形裡，那一種才是宇宙的真實面貌？在窮究一切可能的卡拉比‧丘流形的過程當中，上述這四位提議：或許兩種不同的卡拉比‧丘流形有能造成一模一樣的宇宙空間樣貌。意即：卡拉比‧丘流形與蜷曲空間樣貌或有可能不是一對一，而是多對一的關係。

前文也提過，基本粒子是由「弦」在包括舒展與蜷曲空間的所有維度裡激盪振動形成的 ─ 振盪的模式決定所形成的粒子。

沒提到的一點是：基本粒子會依它們的生成型態成群成族，叫做 "family"。研究發現：基本粒子如何分門別類，和卡拉比‧丘流形在那七個蜷曲空間裡有幾個「洞」大有關係。也就是說，如果我們能找到一切所有基本粒子，將它們成功地分門別類，我們就可以知道，宇宙真正的卡拉比‧丘流形有幾個「洞」─ 雖然還是不知長成什麼樣子，知道它有幾個洞也不錯。可惜這也還不可能，我們尚未能找著所有一切基本粒子。

這裡所謂的「洞」和甜甜圈中心的洞意思一樣。拓樸學上，甜甜圈和馬克杯是同樣的東西 ─ 一個麵團做成甜甜圈後，也可以經由搓揉捏弄，在不撕壞或扯破麵團的條件下，被轉變成馬克杯。

因為二者基本上都是中間有一個洞的三度物﹝在馬克杯而言該洞是即杯邊的耳狀把手﹞。卡拉比‧丘流形只不過是度數和孔洞都比甜甜圈多一些而已。

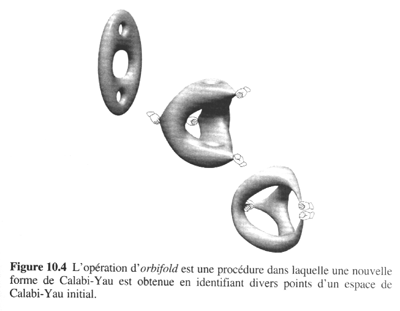
值得一提的是，兩個不同的卡拉比‧丘流形，不論它們在那幾個維度上開洞，只要二者的「總孔洞數」一樣，就會造成一樣多的基本粒子族群類別。

1988 年末，布萊恩‧格林和羅嫩‧普雷瑟在哈佛研究開發將一個已知形狀的卡拉比‧丘流形轉變成另一個未知的卡拉比‧丘流形的數學方法。他們對一種八零年代中期研發出來的，用數學來「玩弄」類如前述甜甜圈麵團，使其形狀、模樣、相貌、孔洞產生變易，叫 "orbifolding" ﹝orbifold 是 manifold ─ 流形的統稱﹞的方法特別感興趣。

因為與瓦法同在哈佛的緣故，他倆在得知上述四人的假設之後，思路遂朝向本文第三段所述之「多對一」關係逐漸整合。

經過數月的研究，格林、普雷瑟越來越傾向於認為：兩個完全相異的卡拉比‧丘流形，如果能用 orbifolding 的方法彼此變化、轉換成功，那麼二者除了在各自形成的宇宙裡會有一模一樣的基本粒子族群類別之外，其他各方面的物理性質也都將完全相同。也就是說，兩種不同的卡拉比‧丘流形可能造成同一種宇宙，條件是 orbifolding 必須成功。他們給這發現取了一個名字：鏡流形。

二人將此一構想告知丘成桐﹝卡拉比‧丘流形的發明人﹞。丘成桐認為他們一定在計算過程中犯了某種錯誤，幾乎不可能完全正確。畢竟，只要一項物理性質不同，兩種卡拉比‧丘流形造成的宇宙即會大相逕庭。況且愛因斯坦發現的空間幾何與宇宙物理間的硬性關聯百年來已經深植人心。再者我們只有一個宇宙，而這個宇宙服膺相對論，弦論鏡流形的事實基礎在那裡？證據又在那裡？話說回來，臆測是一回事，證明又是另一回事。

與此同時，德州州大的菲利普‧坎德拉斯和他的兩位助理研究生以電腦模擬大量卡拉比‧丘流形後發現，幾乎全部的卡拉比‧丘流形都是成雙成對出現的。此一發現正好與「鏡流形」互補：坎德拉斯的研究發現卡拉比‧丘流形有大量的對稱現象，而格林與普雷瑟的計算結果發現對稱的卡拉比‧丘流形會造成完全相同的宇宙。

兩組人馬各發表一篇論文後，弦論的「鏡對稱」從此誕生。

鏡對稱為弦論物理與卡拉比‧丘流形數學的研究工作帶來重大突破。記得人們還在為尋找真實宇宙的確切卡拉比‧丘流形努力不懈嗎？當一個被選來研究的卡拉比‧丘流形的數學運算遇上無可克服的困難時，現在學者們可以改用它的鏡對稱卡拉比‧丘流形繼續下去，並基於鏡對稱原理完全信任最後得到的結果將與使用原來的卡拉比‧丘流形毫無不同。這和利用能量不滅定律證明砲彈飛行拋物線高度之於不同出射角一律相等，較諸使用幾何、三角、牛頓力學等繁複計算更為簡易快捷，是同樣的道理。

鏡對稱是否禁得起考驗？1991 年間發生的一則故事將說明一切。

兩位挪威數學家，蓋爾‧愛靈素爾德和史坦‧阿利爾德‧史特羅姆恰好正在研究一項坎德拉斯團隊同時也在研究的項目。要言之，他們都在尋找某一特定卡拉比‧丘流形內所能容納的球體數目。愛靈素爾德和史特羅姆在花費無數的時間和精力後，得到的答案是 2,682,549,425。坎德拉斯團隊改採該卡拉比‧丘流形的鏡對稱流形，大量簡化計算的難度之後，得到的答案是 317,206,375。

兩個數字的巨大差異在當年柏克來的物理與數學年會上引起廣泛的討論和爭議，許多人將最後真象是否得以大白視為弦論實際可信度的檢驗標準。然而直到年會結束，這兩個數字的差異還是沒有得到解決。

一個月後，愛靈素爾德和史特羅姆在他們使用的電腦程式裡找到了一個邏輯錯誤，程式經過修正後重新運算的結果是：317,206,375，與坎德拉斯團隊的答案完全吻合。

自此之後，許多數學運算業已證明弦論鏡對稱原理的可靠度達到百分之百。更重要的進展是，數學界也已經找到了鏡對稱的理論基礎。利用馬克辛‧康慈維屈、尤里‧曼寧、田剛﹝音譯﹞、李俊﹝音譯﹞、亞歷山大‧基文陶等人的研究成果，丘成桐和連鵬﹝音譯﹞、劉基鋒﹝音譯﹞等人的研究團隊也找出一個卡拉比‧丘流形所能容納球體數目的計算公式，一舉解決困擾了數學界幾百年的問題。

至此，我們可以說，弦論不但為物理提供了一個統合的架構，也與數學在極深的層面上熔鑄在一起。接下來，讓我們看看理論物理如何運用弦論的鏡對稱，來證明空間本身不但可能裂變，也可以癒合，而在事前事後之際，我們的宇宙如何得以安然無恙。