字體:小 中 大
字體:小 中 大 |
|
|
|
| 2009/07/09 16:41:03瀏覽5609|回應18|推薦54 | |
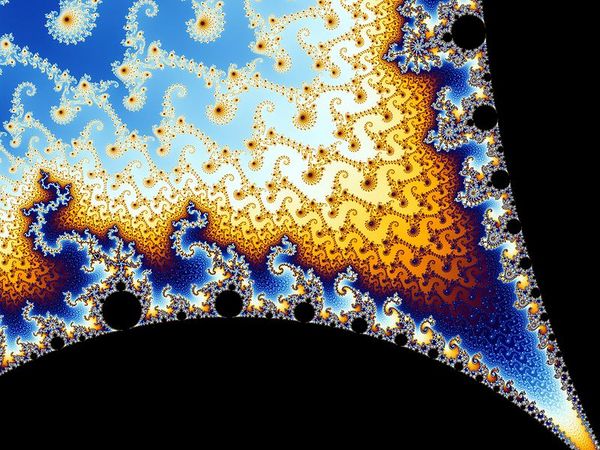
碎形一般是指「一個粗糙或零碎的幾何形狀,可以分成數個部分,且每一部分都(至少會大略)是整體形狀的縮小版」。此一性質稱為「自相似」。碎形的數學基礎可追溯至十九世紀,但「碎形」一詞卻是由曼德勃羅特於1975年提出的,由拉丁文 “fractus” 一詞而來,有「破裂」、「零碎」之意。數學碎形源於方程式的「重覆」,是即基於「遞歸」的一種「反饋」。 碎形通常有以下特質:
因為碎形在所有的大小尺度下都顯得相似,所以通常被認為是無限複雜的。自然界裡一定程度類似碎形的物體有雲、山脈、閃電、海岸線和雪花等等,甚至高麗花菜和綠花椰菜都是。但是並不是所有自相似的東西都是碎形,如實線﹝歐基里德直線﹞雖然在形式上是自相似的,卻缺乏碎形的其他特質,譬如說,它太規則以至可以用歐基里德語詞描述,所以不能被稱為碎形。 碎形的形象可以用電腦軟體產生。電腦軟體產生的碎形雖然不完全符合上述條件,仍被稱為碎形──縱使可能近觀該形象的某一區域,並發現該區域不完全符合碎形的性質。 好了,理論的東西交代完了,讓我們從實際的角度來看到底什麼是碎形吧。點一下這些動態或靜態的圖就知道了。電腦繪製而成的碎形相當漂亮,很是流行了一陣子呢! http://upload.wikimedia.org/wikipedia/commons/e/ed/Phoenix%28Julia%29.gif http://upload.wikimedia.org/wikipedia/en/b/ba/Mandelbrot_color_zoom.gif http://upload.wikimedia.org/wikipedia/en/7/74/Animated_construction_of_Sierpinski_Triangle.gif http://upload.wikimedia.org/wikipedia/commons/f/fd/Von_Koch_curve.gif http://upload.wikimedia.org/wikipedia/en/a/a4/Mandelbrot_sequence_new.gif
|
|
| ( 知識學習|科學百科 ) |