

 字體:小 中 大
字體:小 中 大 |
|
|
||
| 2013/04/26 15:56:16瀏覽15976|回應0|推薦5 | ||
前言 一直以來對於機械人非常感興趣,尤其是在機器視覺這一塊特別的關注,因為欲解決機器人在空間運動的問題,除了利用 MEMS(Micro Electro Mechanical Systems)元件(水平量測的加速度計(Accelerometer)、感測與維持方向陀螺儀(Gyroscope),以及可作為指南針功能的地磁感測器(Geomagnetic Sensor))來解決本身運動感測的問題外,還需要 3D 空間偵測的能力,來解決避免碰撞/接觸的問題。然而在過去依靠雷達或許能夠解決障礙物感測的問題,但是最近出現的 XBox 360 所採行 Kinect 體感控制方案恰巧提供一個新的思考方向。 距離探測 一維距離探測的手段通常有微波(Microwave)、聲波(Sound Wave 或 Acoustic Wave)、紅外線(Infrared)、雷射(Laser)、立體視覺法(Stereoscopic)等。大都屬於三角測距(Triangulation)的應用,但是也有用其他方式的,例如時差測距(Time-Of-Flight,或稱『飛時測距』)。也就是由儀器發射一個雷射光脈衝,雷射光打到物體表面後反射,再由儀器內的探測器接收訊號,並記錄時間,由於光速(Speed of Light) 為一已知條件,光訊號往返一趟的時間即可換算為訊號所行走的距離。 另外一種則是利用『相位差』的方式,這種方法乃是利用雷射照射待測物時的反射光與參考波之間的相位差來求得待測物的距離。首先雷射光源發射一調製光束,檢測器所收到回波信號之相位為 ψ,並與一 local oscillator 產生拍頻 (Beat)信號,此時相位檢測器會測出發射與接收信號間的相位差Δψ ,並藉此計算出距離。但由於相位以 2π 為週期,所以相位測距法會有測量距離上的限制,測量範圍約數十米,精度可達釐米級,但為了提高訊噪比(S/N)有必要多測量幾次,無法做瞬間即時測距。所以這種測距方法多應用在短距離,例如室內裝潢等用途。 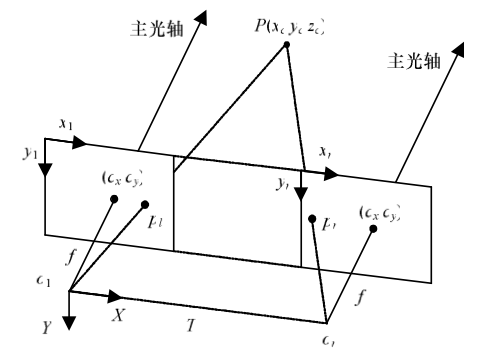
至於立體視覺法的測量方式如右圖所示,使用兩個固定距離的攝影機,平行注視待測物體,然後依照待測物體與主光軸的夾角,便可計算出距離。 以上幾種方法中聲波、紅外線等方式由於發射的測距束波容易發散,所以通常只有厘米級的測量精度。且容易受到干擾,因此應用範圍比較受限制。至於使用微波或雷射在做遠距量測時,則需要考慮包括大氣的折射、電子電路和光學系統的延遲、是否通過日冕或太陽風的路徑、相對論的影響、發射與接收兩端相對運動所產生的都卜勒效應等等。但不管如何雷設和微波因其具有測量距離遠、精度高等優點,目前微波的使用頻率主要集中在23~24,60~61,76~77GHz3 個頻段,波長均為毫米級。 三維探測 我們知道雷射測距儀每發一個雷射訊號只能測量單一點到儀器的距離。因此,如果想要掃描完整的視野(Field of View),就必須使每個雷射訊號以不同的角度發射。而此款雷射測距儀即可透過本身的水平旋轉或系統內部的旋轉鏡(Rotating Mirrors)達成此目的。旋轉鏡由於較輕便、可快速環轉掃瞄、且精度較高,是較廣泛應用的方式。典型時差測距式的雷射掃瞄儀,每秒約可量測 10,000 到 100,000 個目標點。不過在很多案例中,人們以習慣一線形雷射條紋取代單一雷射光點,將雷射條紋對待測物作掃描,這樣可以大幅加速了整個測量的行程。 另外還有幾種方式可以加快掃描的速度,例如使用『結構光源(Structured Lighting)』,將一維或二維的圖像投影至被測物上,根據圖像的形變情形,判斷被測物的表面形狀,可以非常快的速度進行掃描。而『調變光(Modulated Lighting)』則是使用投影機將正弦波調變之光柵投射於待測物體上,調變光三維掃描儀在時間上連續性的調整光線的強弱,常用的調變方式是週期性的正弦波。藉由觀察影像每個像素的亮度變化與光的相位差,即可推算距離深度。調變光源可採用雷射或投影機,而雷射光能達到極高之精確度,然而這種方法對於雜訊相當敏感。 當然我們還是可以用立體視覺法的測量方法來做 3D 空間的量測,只不過此方法在概念上,是類似於人類藉由雙眼感知的影像相疊來推算深度(當然實際上人腦對深度資訊的感知歷程複雜許多),若已知兩個攝影機的彼此間距與焦距長度,而擷取的左右兩張圖片又能成功疊合,則深度資訊可迅速推得。因此法須仰賴有效的圖片像素匹配分析(Correspondence Analysis),一般使用區塊比對(Block Matching)或對極幾何(Epipolar Geometry)演算法達成。所以使用兩個攝影機的立體視覺法又稱做雙眼視覺法(Binocular),另有三眼視覺(Trinocular)與其他使用更多攝影機的延伸方法。 例如 『色度成形法(Shape from Shading)』早期由 B.K.P. Horn 等學者提出,使用影像像素的亮度值代入預先設計之色度模型中求解,方程式之解即深度資訊。由於方程組中的未知數多過限制條件,因此須藉由更多假設條件縮小解集之範圍。例如加入表面可微分性質(differentiability)、曲率限制(curvature constraint)、光滑程度(smoothness)以及更多限制來求得精確的解。此法之後由 Woodham 衍生出立體光學法。 『立體光學法(Photometric Stereo)』,為了彌補光度成形法中單張照片提供之資訊不足,立體光學法採用一個相機拍攝多張照片,這些照片的拍攝角度是相同的,其中的差別是光線的照明條件。最簡單的立體光學法使用三盞光源,從三個不同的方向照射待測物,每次僅開啟一盞光源。拍攝完成後再綜合三張照片並使用光學中的完美漫射(Perfect Diffusion)模型解出物體表面的梯度向量(Gradients),經過向量場的積分後即可得到三維模型。此法並不適用於光滑而不近似於朗伯表面(Lambertian Surface)的物體。 『輪廓法』,此類方法是使用一系列物體的輪廓線條構成三維形體。當物體的部分表面無法在輪廓線上展現時,重建後將遺失三維資訊。常見的方式是將待測物放置於電動轉盤上,每次旋轉一小角度後拍攝其影像,再經由影像處理技巧去除背景並取出輪廓線條,蒐集各角度之輪廓線後即可「刻劃」成三維模型。 這些方式都是基於照片攝影原理,針對同個物體拍攝影像以推算三維資訊。另一種類似的方式是全景重建(Panoramic Reconstruction),乃是在定點上拍攝四周影像使之得以重建場景環境。 Light Coding 技術
微軟的 Kinect 採用的是一家以色列公司 PrimeSense 將其深度測量技術命名為 Light Coding,顧名思義,就是用光源照明給需要測量的空間編上碼,屬於結構光技術的一種,只是深度計算方式不一樣。與結構光法不同的是,Light Coding 的光源稱為『雷射散斑(Laser Speckle)』,是激光照射到粗糙物體或穿透毛玻璃後隨機形成的衍射斑點。這些散斑具有高度的隨機性,而且會隨著距離的不同而變換圖案。也就是說空間中任意兩處的散斑圖案都是不同的。只要在空間中打上這樣的結構光,整個空間就都被做了標記,把一個物體放進這個空間,只要看看物體上面的散斑圖案,就可以知道這個物體在什麼位置了。當然,在這之前要把整個空間的散斑圖案都記錄下來,所以必須要先做一次光源的標定動作。 另外 Light Coding 與傳統的 ToF、結構光技術的不同之處在於,它不需要特制的感光芯片,只需要普通的 CMOS 感光芯片,這讓方案的成本大大降低。同時 Light Coding 技術不是通過空間幾何關系求解的,它的測量精度只和標定時取的參考面的密度有關,參考面越密測量越精確。傳統結構光方法采用三角視差測距,基線長度(光源與鏡頭光心的距離)越長越好。換句話說,不用為了提高精度而將基線拉寬。所以請注意的是 Light Coding 所取得的是『3D 景深影像』與一般的『彩色影像』是不同的,如下圖所示。
基本上這種單純景深影像所取的 3D 資訊並不是非常精準,但是用來做體感偵測卻是足夠了。當然這還得加上『骨架追蹤系統』才能正確判斷使用者的動作出來。 如果你上過他們官網,你一定會他們超高的精準度(0.01mm)而驚訝。網路上有人說是一種利用多普勒效應感知物體移動狀態的技術 sound wave 。也有人說是紅外成像技術(IR)。另一說是『電場成像技術(Electric Field Imaging)』。但具體是什麼樣的技術還真不好說,繼續關注吧! 超遠距測量 雷達遙測 (Radar ranging):精確決定地球與太陽平均距離(一天文單位,1 AU),是量測宇宙距離的基礎。由克卜勒定律 ,可以推算出金星與地球的最近距離約是0.28 A.U.。在金星最近地球時,用金星表面的雷達回波時間,可找出(誤差小於一公里) 1 AU = 149,597,870 公裡≒1.5* 108 公裡 測距適用範圍:~1AU。 恆星視差法 (Stellar parallax) :以地球和太陽間的平均距離為底線,觀測恆星在六個月間隔(地球軌道的直徑),相對於遙遠背景恆星的視差 。恆星的距離d d (秒差距,pc) = 1/ p (視差角,秒弧) 1 pc 定義為造成一秒視差角的距離,等於3.26 光年。地面觀測受大氣視寧度的限制,有效的觀測距離約為100 pc (~300 光年)。在地球大氣層外的Hipparcos 衛星與哈伯望遠鏡,能用視差法量測更遠的恆星,范圍可推廣到1000 pc。 測距適用范圍:~1,000 pc。 光譜視差法(spectroscopic parallax) :如果星體的視星等為mV,絕對星等MV,而以秒差距為單位的星體距離是d。它們間的關系稱為距離模數 mV - MV = -5 + log10d 如果知道恆星的光譜分類 與光度分類 ,由赫羅圖 可以找出恆星的光度。更進一步,可以算出或由赫羅圖讀出恆星的絕對星等,代入距離模數公式,即可以找出恆星的距離。 因為主序星的分布較集中在帶狀區域,所以光譜視差法常用主序星為標的。利用鄰近的恆星,校准光譜視差法的量測。另也假設遠處的恆星的組成與各項性質,大致與鄰近恆星類似。誤差常在25% 以上,。(注:本銀河系直徑約30 Kpc) 測距適用范圍:~7Mpc。 例: 若某恆星的視星等為+15 ,其光譜判定為G2 V 的恆星『i從赫羅圖讀出該星的絕對星等為+5 ,代入距離模數公式15 - 5 = 5 log d - 5 ,求出該星的距離d= 1000 pc = 3260 光年。 變星:位在不穩定帶的後主序帶恆星,其亮度有周期性的變化(周光曲線),而綜合許多變星的周光關系,可以發現變星亮度變化周期與恆星的光度成正比(參見周光關系) 。用來做距離指標的變星種類主要有造父變星(I 型與II 型)與天琴座變星。 測定變星的光譜類別後,由周光圖可以直接讀出它的光度(絕對星等)。由變星的視星等和絕對星,利用距離模數公式, mV - MV = -5 + log10d 即可定出變星的距離。目前發現,最遠的造父變星 在M 100,距離我們約17 Mpc。 測距適用范圍:~17 Mpc。 超新星:平均每年可以觀測到數十顆外星系的超新星。大部份的超新星(I 型與II 型) 的最大亮度多很相近,天文學家常假設它們一樣,並以它們做為大距離的指標。 以造父變星校准超新星的距離,以找出I 型與II 型星分別的平均最大亮度。由超新星的光度曲線 ,可以決定它的歸類。對新發現的超新星,把最大視亮度(mV) 與理論最大絕對亮度(MV) 帶入距離模數公式,即可找出超新星的距離。 II 型超新星受外層物質的干擾,平均亮度的不確定性較高,I 型超新星較適合做為距離指標。 測距適用范圍:> 1000 Mpc。 Tulley-Fisher 關系:漩渦星系的氫21 公分線,因星系自轉而有杜卜勒加寬 。由譜線加寬的程度,可以找出譜線的位移量Δλ,並求出星系的漩渦臂在視線方向的速度Vr, Δλ/λo = Vr/c = Vsin i/c i 為觀測者視線與星系盤面法線的夾,由此可以推出漩渦星系的旋轉速率。Tulley 與Fisher 發現,漩渦星系的光度與自轉速率成正比,現在稱為Tulley-Fisher 關系。 量漩渦星系的旋轉速率,可以知道漩渦星系的光度,用距離模數公式,就可以找出漩渦星系的距離。Tulley-Fisher 關系找出的距離,大致與I 型超新星同級,可互為對照。 注:現常觀測紅外線區譜線,以避免吸收。 測距適用范圍:> 100 Mpc。 哈伯定律:幾乎所有星系相對於本銀河系都是遠離的,其遠離的徑向速度可用都卜勒效應來測量星系的紅位移 ,進而找出星系遠離的速度。 1929年Edwin Hubble得到遠離徑向速度與星系距離的關系 哈柏定律 Vr = H*d 其中
哈柏定律是一個很重要的距離指標,量得星系的遠離速度,透過哈柏定律可以知道星系的距離。 例: 室女群(Vigro cluster) 的徑向遠離速度為 Vr =1180 km/sec, 室女群與地球的距離為 d = Vr/H = 1180/70 = 16.8 Mpc。 測距適用范圍:宇宙邊緣。 紅超巨星:假設各星系最亮的紅超巨星絕對亮度都是MV = -8 ,受解析極限的限制,適用范圍與光譜視差法相同。 測距適用范圍:~7Mpc。 新星:假設各星系最亮的新星,絕對亮度都是MV = -8 。 測距適用范圍:~20 Mpc。 HII 區:假設其他星系最亮的HII區之大小,和本銀河系相當。(定H II區的邊界困難,不准度很高) 行星狀星雲:假設星系行星狀星雲,光度分布的峰值在MV = - 4.48。 測距適用范圍:~30 Mpc。 球狀星團:假設星系周圍的球狀星團,光度分布的峰值在MV = - 6.5。 測距適用范圍:~50 Mpc。 Faber-Jackson 關系:與Tulley-Fisher 關系類似,適用於橢圓星系。Faber-Jackson 關系:橢圓星系邊緣速率分布寬度σ的四次方與星系的光度成正比。 D-σ關系:橢圓星系邊緣速率分布寬度σ與星系的大小D 成正比。 測距適用范圍:> 100 Mpc。 星系:假設其他更遠的星系團,與室女星系團中最亮的星系都具有相同的光度MV = -22.83。 測距適用范圍:~4,000 Mpc 紅位移測距:星體對於我們作相對運動時的光源,會使恆星光譜產生所謂的紅移現象或藍移現象,由都卜勒效應可得知星體的移動速度v,再由 赫伯定律(Hubble's Law):v = Ho × d 即可求得星體的距離d。其中Ho 稱為赫伯常數約在每百萬秒差距50~100公里/秒之間,即星系的距離每增加一百萬秒差距時,它自我們奔離的速度約增加50~100公里/秒。 另外從恆星光譜讀出光譜類型及光度分類,經由赫羅圖 (H-R)決定恆星的絕對星等Mv。我們可直接測得視星等mv,再經由星球距離公式 ( mv-Mv = 5 ㏒ d-5 ),求出距離 d。 例如:某一視星等為+15的恆星,又經其光譜判定為G2V的恆星,亦即可從H-R圖該星的絕對星等為+5,如此可經由星球距離公式 15-5 = 5 ㏒ d-5,求出 d = 1000 PC(秒差距) =3260 LY(光年)。 結論 從上面的描述我們知道每一種空間測量技術,都有其適用的範圍,比方說 Light Coding 就不能用在室外或者光線紊亂的場所。這跟當初所猜想的有些不太一樣,不過這並影響他的價值,特別當我知道它所使用的『散斑干涉法』最初是被認為是一種帶著無用信息的特殊噪聲。但在1969~1970 年,散斑所攜帶的信息得到了應用,發展成為一些測試方法之後,讓我覺得人類的創造力真的是有無限的可能性。所以寫這種文章最大的收穫,不在於搜尋資料、素材的時候吸收多少新知,而是在於當你明瞭多少被隱藏在角落的創意被發掘出來的時候,那種驚喜與讚賞的感覺。 參考連結 更趨實用的體感與MEMS偵測應用解決方案 |
||
| ( 知識學習|科學百科 ) |
















