字體:小 中 大
字體:小 中 大 |
|
|
|
| 2007/04/23 01:27:22瀏覽1552|回應1|推薦7 | |
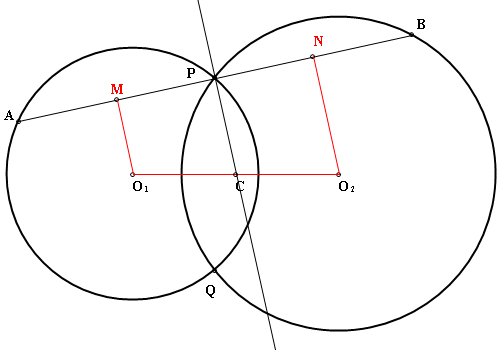
【已知】:兩圓O₁和O₂相交於P、Q二點 【求作】:一直線過P,交二圓於A、B二點,使得AP=PB
【作法】:⒈作O₁O₂的中點C ⒉作通過PC的直線L ⒊再過P點作垂直L的直線M交O₁和O₂2於AB兩點,即為所求。 【證明】:分別由O₁和O₂作垂線交AB於MN ∵O₁M⊥AB,O₂N⊥AB,PC⊥AB ∴O₁M//PC//O₂N 得MP:PN=O₁C:CO₂=1:1→多謝網友最愛小提琴指正。 即MP=PN 又∵O₁M⊥弦AP,O₂N⊥弦PB ∴M、N分別為弦AP和弦PB的中點 故AP=2MP=2PN=PB 得證。
|
|
| ( 知識學習|科學百科 ) |