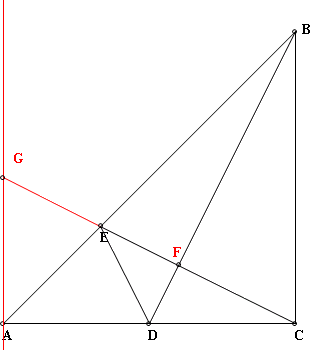
有一等腰直角三角形ＡＢＣ，∠Ｃ為直角，過Ｂ點的一條中線交ＡＣ於Ｄ

，過Ｃ點則有一線段垂直ＢＤ並交ＡＢ於Ｅ。證明∠ＥＤＡ等於∠ＢＤＣ。

設ＣＥ和ＢＤ的交點為Ｆ

過Ａ點作垂線Ｌ⊥ＢＣ，並延長ＣＥ交Ｌ於Ｇ點

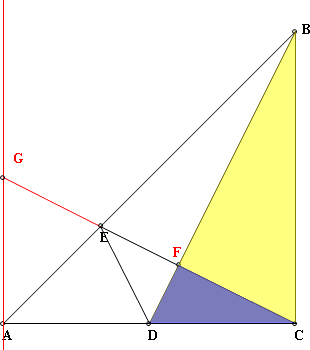
在△ＢＣＤ和△ＣＦＤ中

∵△ＢＣＤ是直角△，且ＣＥ⊥ＢＤ

∴△ＣＦＤ～△ＢＣＤ（母子相似性質）

得∠ＦＣＤ＝∠ＣＢＤ

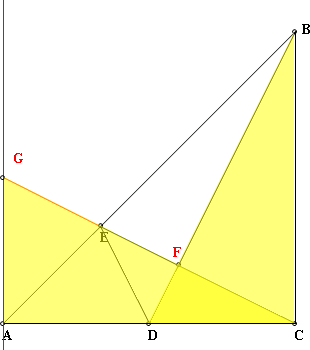
又△ＢＣＤ和△ＣＡＧ中

∵∠ＢＣＤ＝∠ＣＡＧ＝９０，ＢＣ＝ＣＡ，

∠ＦＣＤ＝∠ＣＢＤ

∴△ＢＣＤ≌△ＣＡＧ（ＡＳＡ）

得ＧＡ＝ＤＣ，∠ＢＤＣ＝∠ＣＧＡ......（１）

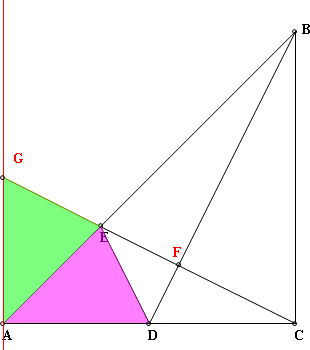
又△ＥＧＡ和△ＥＤＡ中

∵∠ＧＡＥ＝∠ＤＡＥ＝４５，ＡＥ＝ＡＥ，ＧＡ＝ＤＣ＝ＤＡ

∴△ＥＧＡ≌△ＥＤＡ（ＳＡＳ）

得∠ＥＧＡ＝∠ＥＤＡ......（２）

由（１）（２）∠ＢＤＣ＝∠ＣＧＡ＝∠ＥＤＡ　得證