字體:小 中 大
字體:小 中 大 |
|
|
|
| 2006/10/12 09:28:29瀏覽1716|回應0|推薦0 | |
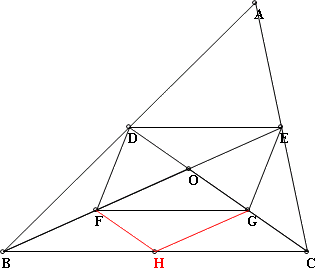
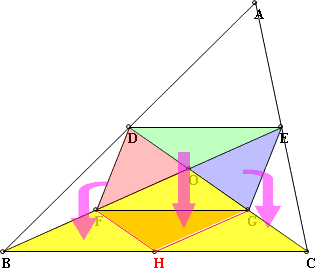
三角形ABC中,D、E分別為AB、AC的中點,BE與CD相交於O,F、G分別為OB、OC的中點,則四邊形DEFG的面積為三角形ABC面積的幾分之幾? 作BC中點H,連接FH和HG
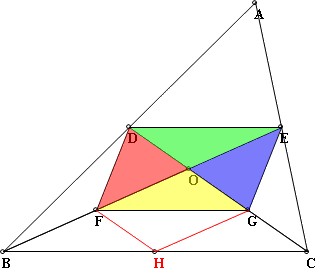
注:△中位線是大陸名辭,我們稱為【△兩腰中點連線】,顧名思義就是△兩個腰的中點所連成的線。 同理 在△OBC中,F、G分別為OB、OC的中點 由(1)(2)我們可以得知四邊形DEFG是平行四邊形
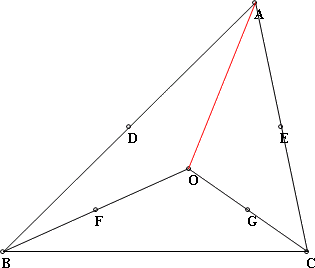
∵CD和BE都是中線 ∴O是重心 故連接OA,OB,OC後
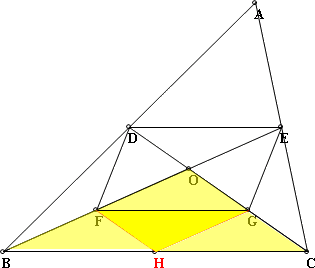
另外在△OBC中,,連接FH和HG後,可以很清楚的發現,△OBC會被分成4塊全等的△
(注:等積換形,顧名思義,就是利用面積相等,可以把幾何圖形換成形狀不同,面積相同的圖形)
|
|
| ( 知識學習|科學百科 ) |