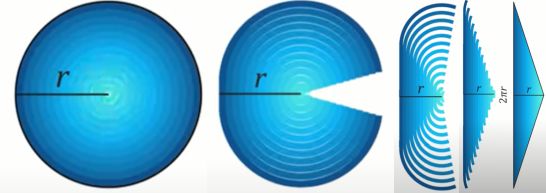
南宋數學家祖沖算出圓周率值準確到第 7位小數點, 他沒有留下資料解說如何做到, 根據我們所知當時的數學技巧, 這是幾乎不可能的事, 後人只能說他是數學天才, 以下是另外兩個有史料可循的巧妙例子. 

要導出圓形面積的公式 A = πr² 需要用微積分, 不過微積分是17世紀時牛頓為了研究物理而發明(註), 之前的數學家沒有這個公式可用, 他們如何算出圓形的面積? 最近得知兩位古代的天才用簡單的幾何觀念, 加上一點想像力輕易算出圓形的面積.

12世紀數學家 Abraham bar Hiyya 的方法是先在圓周的某一點開個口, 然後切開到圓心, 再沿著圓周切出一環環的弧形線以便展開, 完全展開後會形成一個近似三角形的圖形. 這個類似三角形的兩個邊因為弧形線有寬度所以不會是直線, 但是弧線的寬如果能切的非常非常的細, 就會形成一個近乎標準的三角形, 它的高度是圓的半徑 (r), 底邊和圓周相等 (2πr). 三角形的面積是底長乘高度除 2, 所以圓形的面積是 A = (2πr*r)/2 = πr².

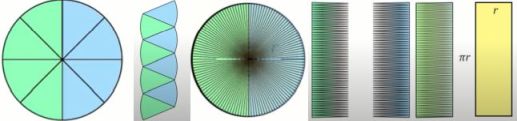
15世紀無所不能的 Da Vinci 也有一個簡單明瞭的方法, 他把圓形平均切成八片, 拿出來湊成一個類似長方形的圖形, 長方形的長不是直線, 但是如果用同樣的方式平均切成很多很多的細片, 就可以湊成一個近乎標準的長方形, 它的寬是圓形的半徑 (r), 長是圓周的一半 (πr). 長方形的面積是長乘寬, 所以圓形的面積是　A = (πr*r) =　πr².

註: 當年牛頓和同時代的德國數學家 Gottfried Leibniz 曾為誰發明微積分抗爭, 歷史學家根據史料判斷他們「各自」研發出微積分, 意思是兩人都說實話, 我推想他們依據前人研究的成果繼續努力, 才會有這樣的巧合, 這件事因牛頓的威名而少為人提.