在 Youtube 上看了火箭叔的水火箭之後相當好奇，其中關鍵詞「極高推重比 (最大靜推力除以最大起飛重量)」，和「極低比沖 (單位質量的推進劑所能帶來的衝量（動量的改變），單位為米/秒（m/s）最大靜推力除以最大起飛重量)」用句人話來描述就是，這個水火箭推力是很夠，但是不持久。所以只能當作一級火箭來用。

另外，影片中提到的「爆沸自生增壓」這個很好理解，那就是儲水罐的高溫高壓液體在釋放到低溫低壓的過程中會產生爆沸，進而使體積劇烈膨脹並於噴嘴處獲得額外的推力。具體我們可以用物質的氣體狀態方程 PV = nRT 來進行計算，其中P為壓力，V為體積，n為物質的摩爾數，R為氣體常數，T為溫度。給定初始條件如下：

壓力P1 = 1 MPa = 1 × 10^6 Pa

溫度T1 = 250攝氏度 = 523.15K

釋放到室溫的最終條件：

壓力P2 = 1大氣壓 = 101325 Pa

溫度T2 = 27攝氏度 = 300.15K

首先，計算初始狀態下水的體積（V1）：

V1 = nRT1 / P1

根據摩爾質量的計算：

M = 18 g/mol = 0.018 kg/mol

質量 (m) = 1 g = 0.001 kg

摩爾數 (n) = m / M = 0.001 kg / 0.018 kg/mol ≈ 0.0556 mol

代入公式計算：

V1 = (0.0556 mol * 8.314 J/(mol·K) * 523.15 K) / (1 × 10^6 Pa)

V1 ≈ 2.793 × 10^(-6) m^3

然後，計算最終狀態下水蒸氣的體積（V2）：

V2 = nRT2 / P2

代入公式計算：

V2 = (0.0556 mol * 8.314 J/(mol·K) * 300.15 K) / 101325 Pa

V2 ≈ 1.215 × 10^(-4) m^3

最後，計算體積增加倍數：

倍數 = V2 / V1 ≈ (1.215 × 10^(-4) m^3) / (2.793 × 10^(-6) m^3)  ≈ 43.57

這是水火箭在噴水之外所額外獲得的推力，但請注意，這個計算結果僅基於理想氣體的狀態方程，並且假設了一定的條件。實際的相變過程可能受到更多的因素影響，如非理想性、水的狀態變化等。因此，這個結果僅作為一個近似值，並且實際結果可能有所不同。

那影片中提到的另一個名詞「機械增壓」則又是什麼回事？原來水火箭上升過程中，作為推進劑的水直接獲得一個加速度，進而可以轉化成推力。

最後我們回到水火箭主要推力的問題上，我們假定儲水罐的內部壓力為　１M Pa，釋放到外部1大氣壓的環境之中，在此假設水的溫度和壓力條件下，水的密度約為1000 kg/m³。

根據托里切利定律是伯努利原理的一個特例，代入相應數值進行計算：

v = √(2 * (P1 - P2) / ρ)

其中：

P1 = 1 MPa = 1,000,000 Pa

P2 = 1 atm = 101,325 Pa

ρ = 1000 kg/m³

代入數值計算：

v = √(2 * (1,000,000 - 101,325) / 1000)

= √(1,898,350 / 1000)

= √1898.35

≈ 43.58 m/s

因此，在給定條件下，儲水罐底部開孔，孔口對外的流速約為43.58 m/s。請注意，這是一個近似值，實際情況可能會受到其他因素的影響，如孔口形狀、孔口尺寸等。

接下來我們想獲得 1.2 的推重比(必須大於1才能起飛)，此時我們假設儲水罐總質量為 1000kg 內含 900kg 水的水火箭，內部壓力為 1 MPa 需要開一個截面積多少的孔呢？此時我們使用質量流率和速度來計算孔的截面積。

推力可以表示為質量流率乘以速度的變化：

F = ṁ * Δv

其中，F 是推力，ṁ 是質量流率，Δv 是速度的變化。

質量流率可以表示為流體通過孔的截面積乘以密度和速度：

ṁ = ρ * A * v

其中，ρ 是水的密度，A 是孔的截面積，v 是速度。

推重比（TWR）定義為推力與重力的比值：

TWR = F / (m * g)

其中，m 是火箭的總質量，g 是重力加速度。

我們要求推重比為1.2，已知 m = 1000 kg，g = 9.8 m/s^2，ρ = 1000 kg/m^3。

將推力的表達式代入推重比的表達式中：

1.2 = (ρ * A * v * Δv) / (m * g)

考慮到火箭從靜止開始升空時速度變化較大，我們可以假設 Δv ≈ v。

化簡得：

1.2 = (ρ * A * v^2) / (m * g)

A * v^2 = (1.2 * m * g) / ρ

A = (1.2 * m * g) / (ρ * v^2)

代入已知值：

A = (1.2 * 1000 kg * 9.8 m/s^2) / (1000 kg/m^3 * v^2)

化簡得：

A = 11.76 / v^2

因此，下方孔的截面積 A 應為 11.76 平方米除以速度 v 的平方。

帶入前面計算出來的43.58 m/s的速度

A=0.00619m^2

然後根據火箭方程，可以進一步推導出火箭的速度變化公式：

v = u * ln(m0 / mf)

其中：

    v 是火箭的速度變化。

    u 是排氣速度（反沖氣體的速度）。

    m0 是起始質量（包括燃料和載荷的質量）。

    mf 是最終質量（僅剩下載荷的質量）。

在火箭的推進過程中，燃料會被耗盡，質量會減少，從而導致速度的增加。

v = 43.58*(1000/100) = 100.346  m/s

此時火箭的升空高度，我們可以使用以下公式：

Δh = (v^2 / (2 * g)) * (TWR - 1)

其中，Δh 是升空高度，v 是速度，g 是重力加速度，TWR 是推重比。

Δh = (100.346^2 / (2 * 9.8)) * (1.2 - 1) = 2,568.7m

當然這只是一個粗略的計算而已。目的只是想知道水火箭的終極性能可以到哪一種程度?

那麼我們可以透過增加儲水罐的內部壓力，或者水溫來加大射程嗎?

透過網路上收集的資料一般來說，水火箭儲水罐的壓力可以在幾個大致範圍內：

• 低壓水火箭：通常使用低壓儲水罐，壓力範圍可以在幾十至幾百千帕（kPa）之間。
• 中等壓力水火箭：一些中等壓力水火箭可能使用高壓儲水罐，壓力範圍可能在幾百至數千千帕（kPa）之間。
• 高壓水火箭：某些高壓水火箭可能使用特殊設計的儲水罐和材料，壓力範圍可能超過數千千帕（kPa）

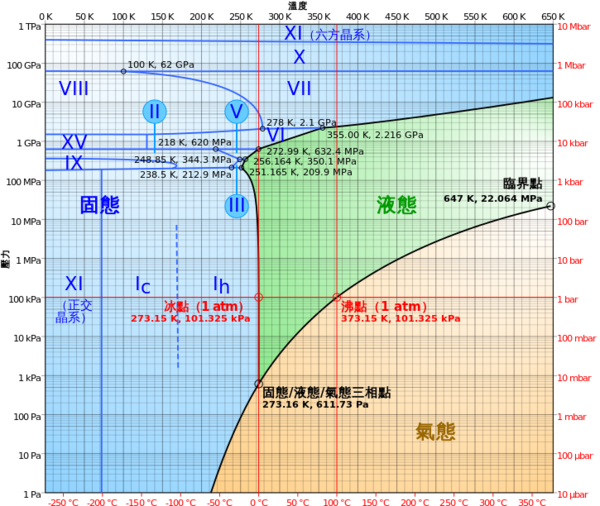
再參考下面水的三相圖

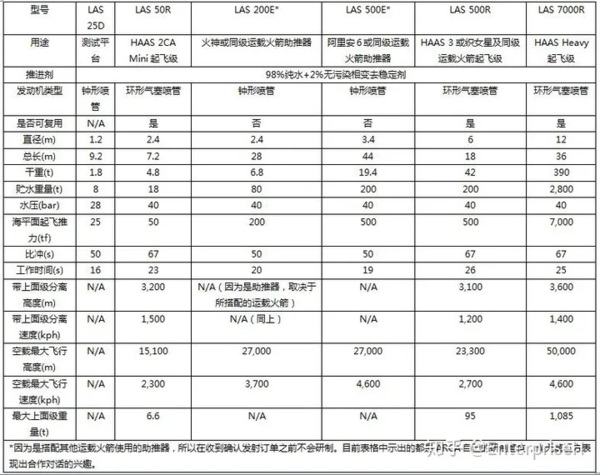
看來水火箭的極限就是如此啊!?

我們再看一下ARCA 公布的LAS 規格

看來作為一級火箭，水火箭還是有點搞頭的!?

參考資料

一大氣壓 (atm) = (76cm)水銀柱高
=(1033.3cm)水柱高
=(1.013)Bar
=(1013百)帕
=(10336)公斤重

1 kg/cm2 約等同於1 大氣壓力（1 atm）

常規氧氣瓶的壓力上限為15Mp（兆帕），換算為大氣壓就是147個大氣壓

一般在國內此類氣體於鋼瓶中之壓力為150kg/cm2

參考連結

有沒有功能很正經但讓人莫名想笑的武器裝備？ 

推重比大於一的固定翼飛機可以像火箭一樣起飛嗎？  

德意志黑科技，世界唯一一款能垂直起降的運輸機 

成飛展示垂直起降隱身戰機專利，可能只是技術儲備，沒必要研製【张斌】 

核動力火箭為何遲遲不露面？技術是個大難題 

【球村】什麼是渦輪增壓？機械增壓？原理如此簡單！ 

神奇的“拉瓦尔管”，为什么能把气体加速到超音速？原理是什么？