Python機器學習筆記（五）：懲罰不合群的人，才有秩序可言-過度擬合（overfitting)與正規化（regularization）

一、何謂「過度擬合」

機器學習的目的很簡單，找到一個演算法模型，先針對現有資料學習，之後當模型接收到新資料時，能對該筆新資料做出正確類別分類或預測。所以要讓一個模型能對「還沒看過」的新資料做出正確的判斷，其前提是先對「已看過」的現有數據，能正確無誤的分析解釋。

但有時我們會發現，模型在學習階段時，雖對現有資料有極佳效能，但在面對新的或未知的數據時，效能卻不好，這種情形，我們稱之為「過度擬合」，也可說該模型有「高變異性」（high variance），其原因是「使用過多特徵」，而產生太複雜的模型。

二、「過度擬合」的例子

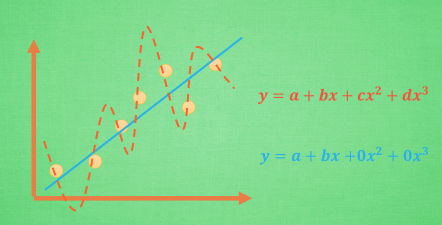
以一個簡單的廻歸問題來看「過度擬合」問題。第一個圖中的粉紅色點點，是已知的現有資料，其內容是由橫軸的x值，與縱軸的y值所組成，我們預期x與y之間具有函數關係，即y=f(x)，當知道x的值之後，我們即能得知y的值，而模型學習的目的，就是利用現有資料，找出x與y之間的函數關係。

假設圖中紅色虛線為模型學習後得出的函數關係，這個x三次方的多項式複雜模型，其函數圖形很完美地通過全數粉紅色點點，其對現有資料的解釋力達到百分百的效能，但其對未知資料的預測卻無多大用處，由於模型高變異的特性，它很難回答以下這個簡單問題：在長期趨勢下，x增加，y是增加還是減少？此時紅色虛線的模型學習結果，即具有「過度擬合」現象。

三、集體秩序 vs 個體自由 - 在「偏誤-變異數（bias-variance）」之間找到平衡點

在一個有「秩序」的環境，事物是按部就班進行，我們也就較易對未知領域進行推測;但若處在詭譎多變、變異極大的環境，既然一切都在變變變，我們就很難推測事物的演變。

再回到第一個圖，其中藍色的直線，是我們希望模型最終學習後能得到的成果：透過一個簡明的「秩序」規則，我們即能掌握未知動態。但這條藍色直線並未通過多數的粉紅色點點，這代表模型在尋求「秩序」過程中，犧牲了每筆資料的「個別特性」，並以「噪音」（noise）來形容這些「個別特性」，雖然這些「噪音」造成模型推測值不等於實際資料的「偏誤」，但我們對造成「偏誤」的原因並不感興趣，所以才將其稱為「噪音」，並從模型中抹除這些「噪音」的影響力。

通常一個模型的學習效果，「低偏誤」與「低變異數」二者無法兼顧，須在二者間做一取捨。

四、懲罰不合群的人 - 正規化

一直在重複說，模型學習、模型學習•••，模型是如何進行學習的？簡單說，就是不斷調整模型參數的權數值，使模型推測值與實際值間的差異，達到最小的境界，這個過程我們稱之為成本函數（模型推測值與實際值間的落差）的極小化。

1.單純成本函數極小化-產生「無偏誤-高變異」模型結果

再回到第一個圖形，假設a、b、c、d分別為模型截距項、x一次項、x二次項、x三次項的權數值，一開始模型會隨機賦予a、b、c、d初始值，再依據此時模型推測值與實際值間的差距，調整a、b、c、d數值，一直調整到使模型推測值=實際值，即成本函數=0，這時模型會推導出通過所有實際值粉紅色點點的紅色虛線，其成本函數雖極小，但其高變異特質並非我們想要的結果。

2.正規化：極小化（成本函數+成本懲罰）

所謂正規化，就是加入成本懲罰，用來懲罰極端參數權重的機制。此時當我們使模型推測值=實際值，讓成本函數=0，但加上成本懲罰後，此時（成本函數+成本懲罰）加總後的結果不一定能達到最小的結果。

在求解（成本函數+成本懲罰）極小值的迭代過程中，加入的成本懲罰機制，會使極端參數權重，如x三次項的d或x二次項的c朝0收斂，最後得到圖中藍色直線，一個低變異但有偏誤的模型學習結果。