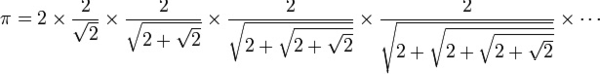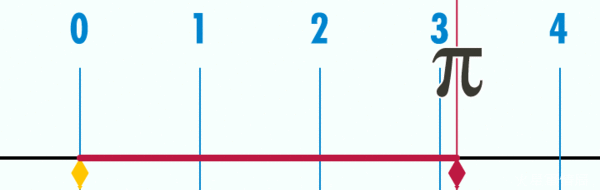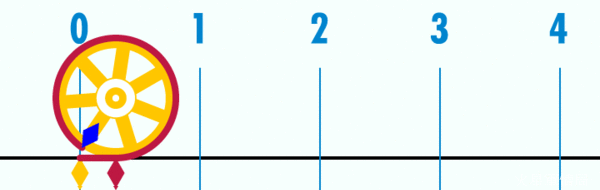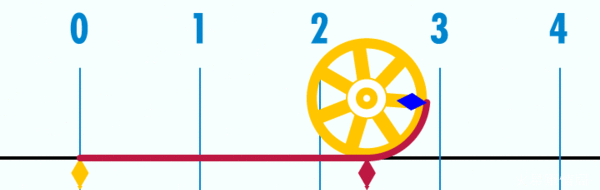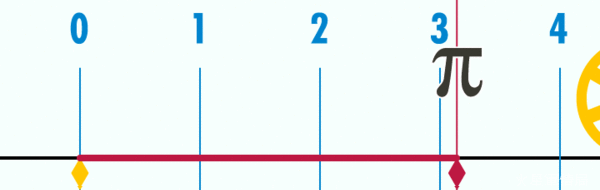
這個星期六早上9:26你要做什麼？建議你把這段時間空下來，因為這一天是2015年3月14日，那個時刻可以寫成3.14.15 9:26。覺得面熟嗎？對啦，這就是圓周率π ＝3.1415926...！每年的3月14日是「圓周率節」（Pi Day)，今年正逢20“15”年，是一世紀只有一次的特別圓周率節，當然要親朋好友團聚，大吃這個節日的傳統食物：一個又大又圓的派（pie）！

（圖片來源：維基百科）

如果有人基礎數學已經還給老師，趕快複習一下：圓周率是圓形的周長與直徑的比：

這個數字對人類文明太重要了，若是沒有準確的圓周率，做出來的圓形物體就有誤差，更何況圓形代表「完美形狀」，古人甚至認為它有神聖的含義。圓周率對今天的我們更重要，因為它是所有圓周、簡諧運動的基礎，任何和頻率有關的事物（振動、通訊、影像...）都和它有關，如果圓周率有明顯誤差，你的電話、電腦不過是個廢物。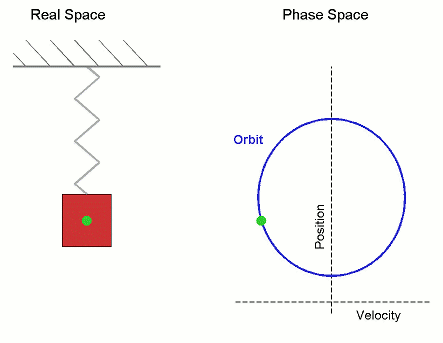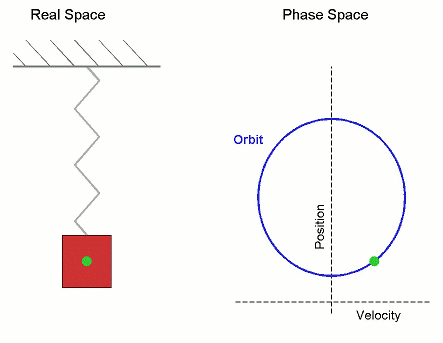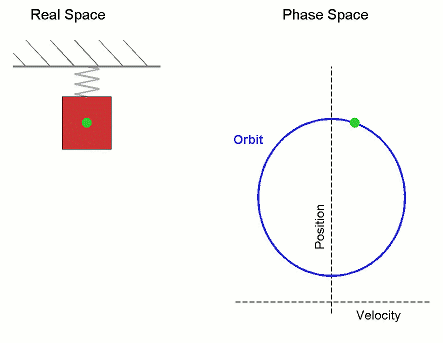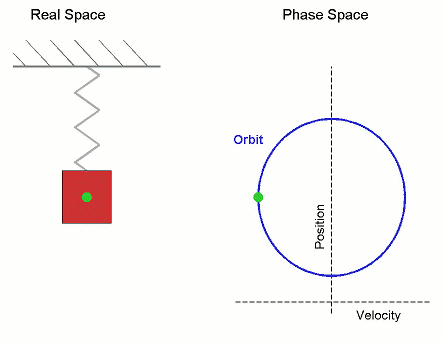

生活中的許多事物都是周期性的，都和圓周率脫不了關係。（圖片來源：維基百科）

人類文明初期就發現不論大圓小圓，周長與直徑的比例都一樣。西元前兩千年前的巴比倫記載這個比例是25/8=3.125。中國西漢末年的《周髀算經》記載「周三徑一」，可見那時的中國人用簡單的整數3代表π。

古時候沒有電玩，有些智商比較高的宅男就關在房間裡，絞盡腦汁求出π的數值。真的，要很的宅的宅男才有耐心做得到。

古希臘的大數學家阿基米德利用外切和內接正多邊形「夾住」中間的圓形，圓形的周長不會超過外切多邊形，卻又比內接正多邊形的周長大，就可以算出圓形周長的範圍。因為多邊形的周長可以用三角的「畢氏定理」算出來，而且多邊形的邊數越多越趨近圓形。阿基米德從六邊形、十二邊形...算到了96邊形，發現π介於22/7和223/71之間（3.14084和3.14285之間）。你有這種耐心嗎，不妨試試把一個圓形切成96等分，看看是不是會被煩死。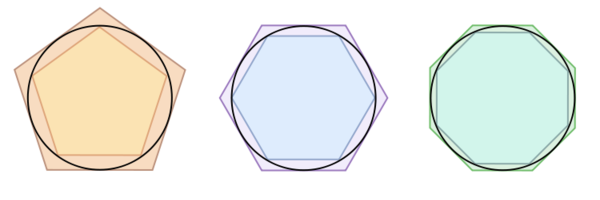

阿基米德用外切和內接正多邊形「夾住」裡面的圓形，多邊形的邊數越多就約接近圓形，他最後使用96邊形，後來的劉徽當然不知道阿基米德是什麼碗公，不知道可以用內接和外切多邊形做三明治，但是卻使用了3072邊形。（資料來源：維基百科）

中國魏晉時期的數學家劉徽用內接3072邊形得到π≈（趨近於）3927/1250=3.1416，給今天的高中生寫作業已經綽綽有餘。200年後南北朝的祖沖之幾乎是中國的民族英雄，他算出π≈355/113＝3.1415926。史書並沒有詳細說明他是怎麼算的，但是後人估計他需用內接24576邊形才能達到這個精確度。嗎呀，他真是有耐心，天天吃飽沒事做。這個精確度在一千年以後才被打破。

想要打破這種紀錄真不是人幹的，15世紀點荷蘭數學家Ludolph Van Ceulen花了40年時間，在臨終前計算到正2⁶²邊形，得出了小數點後35位的準確度。更可憐的是17世紀的William Shanks發表了小數點後707位的圓周率；後來證明由第527位以後是錯的。N年的青春全白費了，如果他地下有知，一定會大罵髒話。

後來的數學家發現更好更快的方法，不再用阿基米德的幾何法土法煉鋼。1593年的Francois Viète就發現可以用無窮級數算出圓周率：

計算到第25項就準確到小數點後第15位，只要算幾天就可以抵過前人好幾年的努力。後來更好的方法不斷推陳出新，16世紀的重量級數學家Euler發明的辦法，只需一小時就可達到小數點後20位的精確度，他也定調把“π”這個希臘字母代表圓周率。

時光荏苒，歷史上偉大的宅男們，謝謝你們鞠躬盡瘁的貢獻，可是我們不需要你了。歡迎進入電腦時代！

現代電腦先驅von Neumann等人在1949年利用世界上第1台真正的電腦ENIAC ，只用了 70 小時就算到小數點後2037位。其實精確到小數點後第40位就夠人類使用，不過為了人爽，就繼續算下去吧。到2014年底為止電腦已經算到小數點後第13,300,000,000,000位，如果把這個數字印成一般字體排好，它的長度可以環繞地球1000次！圓周率是一個無理數（或更精確一點，超越數），是沒有終點的，地球人甚至外星人的電腦都可以永無止境的算下去，直到宇宙的末了，即使用盡宇宙裡每一個原子當作一個位元（bit）也裝不下這個數字。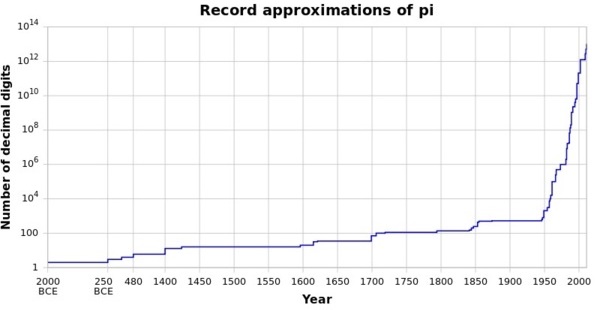

人類追求圓周率精確度的歷史，1950年以後藉著電腦突飛猛進。（資料來源：維基百科）

電視影集《Star Trek》有一集的劇情描述企業號上的電腦被外星人入侵，史巴克就要求電腦算出圓周率的最後一位數，好把它操死。

有人知道“3.1415927>π>3.1415926”怎麼翻譯成文言文嗎？從《隋書》記載祖沖之的事上可以拿到正解：： 「圓徑一丈，圓周盈數三丈一尺四寸一分五厘九毫二秒七忽，朒數三丈一尺四寸一分五厘九毫二秒六忽，正數在盈朒二限之間」～～徹底被打敗，做數學還要這麼文謅謅。

西雅圖市中心的雕塑“Pie in the sky"

想要知道這個節日的典故很如何慶祝嗎：可以參考看雲的《一起來慶祝“π節”（圓周率日）》

參考資料：

• 圓周率的歷史，數學資料庫。非常詳盡又好懂的解釋，我這篇文章的主要來源。
• Pi，Wikipedia.
• Chronology of computation of π，Wikipedia.