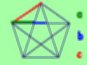
第二組科學營紀錄 ~ 黃金比例&費氏數列的奇妙關係

今天是科學營的第一天~數學營,學校邀請到一位厲害的講師"陳彩鳳老師"來和我們討論有關黃金比例&費氏數列的奇妙關係,老師精心安排的內容,使我們考試科目中的夢魘,死板的數學活了起來,讓我們體會到數學的"生"!

老師並不是一開始就和我們述說黃金比例&費氏數列,而是使用層層引導的方式,列了許多標題,將我們慢慢帶入黃金比例和費氏數列的奧妙中。

一開始便是"有容乃大"告訴我們數學是活的!而非死的;學數學要好奇,而非厭倦!其實我們的日常生活中就處處與數學息息相關,每個人對於數學的感覺也不盡相同,就如同疊羅漢一般,有人喜歡站在最頂端,有人喜歡站中層的位置,有人卻喜歡站在最下層,擔當別人疊上去的橋樑;但不管如何只要每個人盡到自己的本分和義務,排出來的疊羅漢都是美的!

講到"超可怕的人工智慧"在[ http://0rz.tw/ef0u4 ]中,要我們在心理想一個東西,接著電腦會開始問問題,且電腦會在20題內猜出我們心裡想的東西,事關於人工智慧的高深,老師說此遊戲是關於"十分逼近法",電腦利用此類似方式,層層逼近,進而猜出我們心裡我想的東西,人工智慧非常神奇。接著便問我們1元硬幣直徑有多大?是2cm,其實我們在深入學習數學的當中,卻時常對於我們週遭的最基本數學給忽略了!學數學的另一項重要因子就是"觀察",觀察週遭的一切事物,因為任何數學理論都是由生活為出發點,而整理出來的!且身分字號是可猜出來,如果我們有用心觀察其中的關係。

爲了貼近生活,老師準備了許多鑽有1元硬幣大小的紙,試試看能否將1元.5元.10元.50元的硬幣穿過此洞?其實全都可以,就像學數學一樣,我們不能被侷限於一個小框框中,那個1元硬幣的小洞,在經過翻轉.摺疊.拉合和擠押後,發現洞由圓形變為長條狀的,也就是原本1元的圓周除2,變為此長條洞的長,此長度大於50元的直徑,則所有的硬幣皆可通過。還有講到平常店家的促銷手法相當於幾折,像買1送1=5折,買3送1=75折,買4送1=8折。另外一公畝=100平方公尺=10m乘10m 約為一間教室大小,10m也就相當於10個人手拉手,都很有趣味性!

更舉例電影"絕地重生"中的一段話說:"逃犯人高5 呎9 吋,以徒步逃了2小時15分鐘。"而指揮官立刻派人地毯式搜尋10km範圍內。因5 呎9 吋約175.26cm,而徒步跑每分鐘約114步,每步約60cm,則由此算,每小時可走4km,2小時15分鐘約可走9.54km,所以指揮官下令搜尋10km範圍內,是經過複雜估計計算的,電影並不是隨便寫寫的!

接著討論到分類和規律,要我們試著以一個小學生的邏輯找出分類規律

<1>   1,3,7,8          ---------一聲

         0        ---------------- 二聲

         5,9        -------------- 三聲

         2,4,6         ------------四聲

<2>   M T W T F _ _          ---------S  S <星期1~7>

<3>   O T T F F S S _ _ T   ---------E N <1~10>

<4>   2,5,10,17,__,41,58......      ---------28<從第一個數開始後面每2個數間的差 +3,+5,+7,+11,+13,+17......皆為質數>

另外還講到許多的規律問題,像三角階梯的階乘關係;圓平面分割的階差關係。但老師也說,雖然在一數列的前端找到一種看似對的規律性,並不代表那一定是對的!數學可假設,但要不斷的去印證,像數列"1,2,4"的下一個數,可為7 則成階差,亦可為8 成等比,還有各式各樣的答案,都具有它的規律性。

在中場休息中,老師還讓我們腦力激盪,赤道長40000km,若用一條比赤道長1m的繩子,平行繞於赤道外,如同心圓般,問:老鼠可從赤道和繩間的縫穿過嗎?可以的!因兩圓差1m,則1/圓週率˙2 = 約0.159m = 15.9cm = 兩圓間的距離,15.9cm是夠一隻老鼠通過的!同理,赤道長加4m人就可滾過!

黃金比例的主題就由簡入深,逐漸浮現。大家都知道黃金比例 : 1.61803...... , 但它在數學中有許多式子和形狀和定理,運算到最後都會非常神奇地趨近於此數,老師舉了很多例子:

<1>正五邊形中畫出由五條對角線構成的星形,星形中也是正五邊形<如上圖>,此圖中隱含著黃金比例, c = a+b ,且每一條對角線為正五邊形邊長的(1+根號5)除2,且不斷往內畫星形和五邊形,亦符合此原則,則為黃金比例!

<2>政府規定山坡地坡度30度以上禁建,超過30度時,就不好開發,也可利用tan值和水平距離和垂直距離來算坡度。

<3>一般影印紙和報章雜誌用紙的大小,也符合黃金比, 長:寬=根號2 : 1 ,此比例好拿.好看,是由比爾蓋茲所訂定。

<4>在同一線段上,畫滿相切的半圓,則不論弧線如何彎曲,皆一樣長。

最後老師又問:有一真分數,分子和分母差13,化為小數四捨五入後取到小數點後第2位為0.62,也和黃金比1.61803有關。答案為21/34,也就是從費氏數列出來的!

費氏數列:1,1,2,3,5,8,13,21,34,......<相鄰兩數,後數/前數,愈趨近於黃金比例>

在此4小時的講課也接近尾聲,很感謝陳彩鳳老師給我們一課數學的洗禮,發現其實數學佈滿我門生活週遭,處處可見,如果用心觀察,處處都有新發現,除此之外,我還找到一本書~"黃金比例:1.61803......的秘密"是對黃金比例深入了解的管道!老師最後還提醒我們研究數學的問題要"for what & what for"!

2007 . 2 . 5 .by princess<19>孟孟