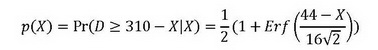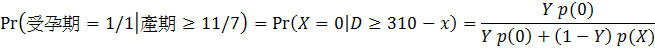Dear Abby是1956年開始發行、流傳甚廣的美國顧問專欄，起初的作者Pauline Phillips已在2013年過世，現由她女兒繼續以同名執筆經營。Dear Abby經常為讀者提供諮商，為他們解決各種疑難雜症。下面這封讀者來函曾被列入統計學教科書裡，我也常用來作為基本統計學的教材。

我把這個材料給學生看，然後引用醫學知識，說受孕至生產時間呈常態分配，其平均數為266天、標準差為16天，要他們計算女人懷胎最少310天的機率，他們算出答案為0.003時，都發出會心的微笑。

現在我把這題目略改如下：

某貝氏統計學家與老婆婚姻生活一向平靜無波。某年元旦，兩人慶祝新年，決定生產報國，嗣後依然恢復平靜無波的生活。該年11月7日，老婆產下一女。

老公是一位統計學家，善於數算，老婆生產後，他推算如果此女確為從他所出，則老婆懷孕時間長達310天。根據醫學知識，一般婦女懷孕時間呈常態分配，其平均數為266天，標準差為16天。老公推算懷胎至少310天的機率是0.003。

統計學家老公算出這個機率後，不禁眉頭一皺。他想：0.003是小機率事件，比統計推論的顯著水平0.05還小很多，怎麼就發生在自己家裡？此機率是由老婆受孕日期在1月1日的假設推算出來，因機率甚小，依「以否定後件來否定前件」(modus tollens)的命題邏輯，不能接受這個假設，然則難道自己戴綠帽了！當下咬牙切齒，拍桌大罵老婆。

不過老公畢竟有些學問，他再仔細一想：0.003的機率雖然小，但若樣本夠大，這麼小的機率也會發生在很多人身上。以台灣每年大約有20萬新生兒來說，假設大多數為單胞胎自然生產，則每年約有600個媽媽懷孕時間會長達310天或更久。大樂透每注中頭獎的機率0.00000007比0.003要小很多，而經常都有人中獎。相較之下，老婆中到0.003機率的大獎，也沒什麼好奇怪的啊。統計學家老公想到這裡，不禁笑開了嘴：這寶貝女兒，說不定還會給自己帶來財運呢。立馬到小7買了十張樂透。

第二天樂透開獎，十張全部槓龜，統計學家老公又懊惱起來了。他想：雖然說經常都有人中樂透，偏偏自己從來沒中過，連每期對幾十張統一發票都難得中到200元的小獎，哪有說這0.003機率的事件就輪到我？畢竟「個人中獎」和「有人中獎」是不同的事件，不能一概而論。那怎麼辦呢？究竟我該不該相信老婆？還是乾脆去查驗DNA算了？

貝氏統計學家老公靈光一閃，發現自己面臨的難題其實並沒有那麼簡單，而應該用貝式定理來推算。他這樣想：0.003是在老婆未出軌的假設下計算的，因此它是一個條件機率：

Pr(產期≥11/7|受孕期=1/1)= 0.003

但對一個貝氏統計學家而言，更該問的問題其實是：既然小孩是在11月7日出生，那老婆未出軌的機率為何？換句話說，更重要的機率應該是上面那個機率的反機率：

Pr(受孕期=1/1|產期≥11/7)=？

這就是老婆未出軌的後驗機率。以貝氏統計學家的專長，老公知道要算這個後驗機率需要考慮兩個變數：

1. 老婆在1月1日之後，是否有出軌受孕的機會？假設真正的受孕期是1月1日之後的第X天。X=0代表老婆沒出軌，受孕期真的是1月1日；X>0代表老婆在1月1日後出軌才受孕。
2. 自己一向對老婆有多少信心？依自己的主觀判斷，老婆未出軌，即X=0的機率有多少？假設X=0的機率為Y，X>0的機率為1-Y，則Y越接近1信心越高，越接近0信心越低。Y是X=0的邊際機率，1-Y是X>0的邊際機率。這邊際機率也就是貝氏定理所謂的先驗機率。

另外，如果我們以D來代表懷孕時間，則不論受孕期X是哪天，小孩在11月7日出生時，D都等於310-X。我們以D<310-X代表產期在11月7日之前，D≥310-X代表產期在11月7日這天或這天之後。D≥310-X的機率顯然與X有關，我們用p(X)來代表此一條件機率：p(X)=Pr(D≥310-X|X)。因為懷孕時間呈常態分配：D~N(266,16)，我們可以導出 

這裡Erf()是誤差函數；當X=0時，p(0)=0.003。

考慮這些變數後，我們可以用下列矩陣來呈現這個貝氏定理問題：

關於貝氏定理的算法，請參考我寫的《貝氏定理在生活中很有用，可是它到底怎麼算？》。老公要求的後驗機率是：Pr(受孕期=1/1|產期≥11/7)=Pr(X=0| D≥310-X)。要求這個機率，首先必須把上表中「行」的條件機率轉化成聯合機率。這個只要記得「聯合機率等於條件機率乘以條件本身的邊際機率」的口訣就可算出如下：

算出聯合機率之後，再用「條件機率等於聯合機率除以條件本身的邊際機率」的口訣就可算出所要求的「列」的條件機率：

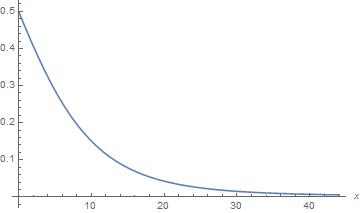
把前面算出p(0)和p(X)套入上式之後，我們可以看到後驗機率Pr(X=0|D≥310-X) 是X和Y的函數，為了更容易分析這函數，我們先把Y值固定，再看它如何隨X值變化。

首先，假設老公對老婆只有Y=0.5的信心，則後驗機率的函數圖形如下:

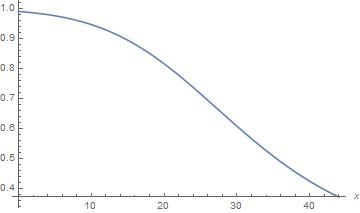
這個圖顯示如果老公本來就對老婆疑信參半，則當老婆在1月1日之後的一個半月之內有出軌的機會時，老公對老婆的信心會隨著X的增加而急速下降。當出軌的機會X增加到預產期(1月1日後第X+266天)越接近11月7日時，X>0顯得越「正常」而X=0顯得越「不正常」， 因此老公的信心會越低，疑心越重。特別是當老婆在二月(X>30)有出軌的機會時，那意謂著11月7日正是預產期的一個標準差(16天)之內，老公的信心會降至幾乎為0。

其次，如果老公平常對老婆有極高的信心，例如Y=0.99，則後驗機率的圖形為

這圖顯示如果老公平常對老婆有充分的信心，則這信心隨著X的增加會下降得比較緩慢。即使到二月初才有出軌機會，也就是預產期開始接近11月7日時，老公對老婆仍然維持著0.6以上的信心。甚至當X=44，即預產期恰恰為11月7日時，老公的信心仍在0.37的水平。

雖然信心不至於完全崩潰，但畢竟也會隨著X的增加而減小。老公算出貝氏後驗機率後應該了解，310天是超乎尋常的懷孕時間，除非本來對老婆就有百分之百的信心，否則信心一定會下降的。雖說這只是「信者恆信，不信者恆不信」的貝氏詮釋，但在這個案例，信者卻必須要完全相信才能恆信，而不信者只要心中有點疑竇，終究會不信。

貝氏統計學者數算到這裡，長嘆了一口氣：「還是去查驗DNA吧！」