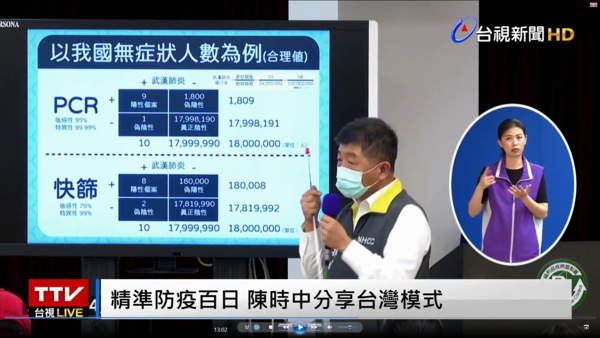
防疫中心指揮官陳時中在4月28日的例行記者會中，就新冠病毒普篩的偽陽性、偽陰性問題以實際數據進行了分析。他把普篩假想對象分為兩種不同人口：呼吸道症狀就醫人口、無症狀人口。再就每一種假想對象依據台灣疫情提出兩種盛行率的估計：極大值、合理值。如此，假想對象×盛行率一共有四種組合。陳時中再對每一種組合分別提出關於PCR（核酸檢測）和快篩兩種檢測工具精密性的分析。

陳時中的數據顯示快篩在這四種組合都會產生數萬到數十萬的偽陽性，而連PCR都會有數百到數千的偽陽性。這就引起了一個問題：如果快篩的精密性那麼低，而PCR也有問題，那防疫中心之前採檢的結果還值得信賴嗎？那四百多個確診個案難道沒有偽陽性嗎？本文針對這個問題提出貝氏統計學的解釋。

陳時中在分析中提供了PCR和快篩的特異性和敏感性，分別為：

• PCR：特異性=0.9999，敏感性=0.95
• 快篩：特異性=0.99，敏感性=0.75

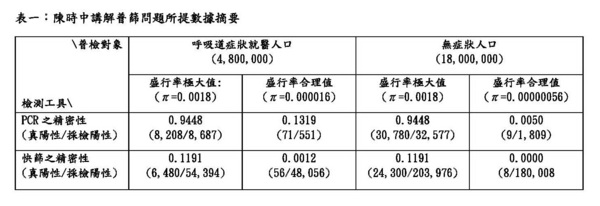
在固定這些參數值之後，陳時中報告了四種組合中每一組合的真陽性、偽陽性、偽陰性、真陰性的數目。他在報告中特別著重當採檢結果為陽性時，真陽性與偽陽性的數目。

我們知道醫檢學中的所謂「敏感性」是真正帶原者之中真陽性的比例。把比例等同機率，則敏感性就是當受檢者是真帶原者時，採檢結果為陽性的機率：

敏感性=Pr(採檢為陽性｜受檢者是真正帶原者)

因此，採檢為陽性之中真陽性的比例，轉換成機率的概念，便是敏感性的反機率。這個反機率在數據科學有一個專門的名稱，叫做「精密性」（precision）。

精密性=Pr(受檢者真正帶原｜採檢為陽性者)

數據科學把敏感性叫作「召回率」（recall），召回率與精密性共同決定了檢測的準確度（accuracy）「F1分數」（F1 Score）。醫檢學雖然沒有使用「精密性」這個名詞，但陳時中的講解所著重其實便是精密性的討論。

精密性是敏感性的反機率，那麼這個反機率如何計算？反機率的計算要用貝氏定理，但光知道敏感性是不夠的，必須還要知道「特異性」及「盛行率」，其中盛行率便是貝氏定理的所謂「先驗機率」。陳時中的報告提供了各種組合的敏感性、特異性、及盛行率，因此可以算出精密性。

下表顯示陳時中報告中PCR及快篩的精密性:

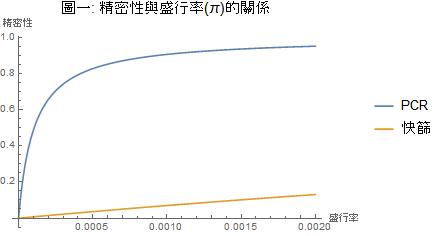
除了PCR在盛行率極大值時以外，這些精密性數值不但小到令人驚訝，而且令人疑惑：如果盛行率π=0.000016及π=0.00000056的估計真的是「合理」的，那不但快篩，連PCR的精密性都低到慘不忍睹的地步，那這樣的檢測工具還有任何用處嗎? 那豈不是防疫中心疫情開始以來所檢驗出來的所有結果都不值得信賴了？

要解開這個疑惑，必須進一步了解貝氏定理所謂「先驗機率」的意涵。

首先，先驗機率既然是「先驗」的，它就不是客觀的經驗事實。 先驗機率可以用先前(例如別的地區或人口)的數據來估計，但它基本上反映了貝氏統計學者的主觀「信仰」（belief）。在醫學檢測，這個「信仰」，除了醫學文獻、臨床經驗外，它通常還要靠著問診、疫調等專業程序來建立，也就是醫檢人員必須要評估受採檢對象的旅遊史、接觸史、疾病史、健康狀況、有否相關症狀、乃至於飲食作息等等資訊才能建立。 換句話說，先驗機率的建立與受採檢對象的「脈絡」（context）息息相關。採檢對象的脈絡不同，先驗機率也會不同。

既然盛行率是先驗機率，而先驗機率會隨著採檢對象的脈絡而改變，那麼盛行率也會隨著採檢對象而改變。檢測的精密性又與盛行率有關，那精密性自然也會隨著盛行率而改變。圖一顯示了在給定的敏感性和特異性之下，PCR、快篩兩種檢測工具的精密性與盛行率的關係：

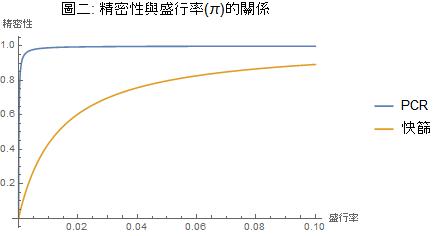
圖一顯示盛行率π=0.0018（陳時中估計的盛行率極大值）時，PCR的精密性在94%左右，快篩的精密性則約12%。圖中也可看出：在盛行率π=0.000016或π=0.00000056（陳時中估計的盛行率合理值）的時候，PCR和快篩的精密性都是很小很小的。這些精密性的準確值在表一都有，但圖一更清楚地顯示了精密性在盛行率小於0.0020的範圍內隨著盛行率漸增的趨勢。

現在可以回答前述的問題了：既然合理的盛行率估計值導致PCR和快篩都是那麼小的精密性，那麼不論是快篩或PCR不是都沒有用嗎？防疫中心之前的採檢不會有很多偽陽性、偽陰性嗎？

這個問題的回答是：精密性低的癥結不是在於採檢工具的品質——就敏感性和特異性而言，防疫中心所使用的PCR和快篩的品質都是極佳的——而是在於（假想中）對廣大對象在缺乏足夠脈絡資訊之下做了無厘頭的採檢！

因為對於一千八百萬無症狀人口沒有任何問診、疫調，防疫中心只能以既有確診案例數來估計這個人口的盛行率而定其合理值為π=0.00000056。是因為先驗機率未能包含有用資訊，而不是檢測工具的品質，導致了精密性低落到幾乎為0。

這個解釋，只要看陳時中把採檢對象限制在呼吸道症狀就醫人口所做的分析就立刻得到驗證：因為這個群體看過門診，確定有疑似症狀出現，防疫中心可以用這個脈絡資訊把盛行率的合理值提高到π=0.000016。此時同樣品質的PCR的精密性就從0.0050提高到0.1319，而快篩的精密性也從0.0000提高到0.0012。這微弱的改進誠然還是嚴重不足，但它可以讓我們看見脈絡資訊的重要性。

另外，我們也可以從表一及圖一看到：不論對象是無症狀人口或呼吸道症狀就醫人口，如果都用極大值π=0.0018來估計盛行率，則同一檢測工具的精密性不會改變。此時PCR的精密性可以高達0.9448，看似可以接受，但在廣大的採檢對象中，仍然會有不少的偽陽性案例。

以上的分析告訴我們：對廣大人口無緣無故實施普檢，檢測結果的精密性可能不足信賴。這不是檢測工具品質不佳的問題，而是脈絡資訊不足的問題。如果社區感染的現象明顯到防疫中心對盛行率的估計可以提高，則我相信他們也會考慮普檢。

圖二把圖一的橫軸延伸到π=0.1。從圖中可以看出：當盛行率的合理估計達到π=0.01時，PCR的精密性就很接近99%了。只是如果普檢要仰賴快篩，則43%的精密性還是有所不足。

防疫中心目前使用快篩應該都是有相當的脈絡資訊才使用，當脈絡資訊指出特定對象（例如有明顯症狀的入境旅客、與確診個案有親密接觸的人士）受感染的先驗機率甚高時，使用快篩當然是可以接受的。例如當合理懷疑某對象受感染的先驗機率達到π=0.1時，圖二顯示PCR的精密性幾乎是100%，而快篩的精密性也近乎90%了。

這就是貝氏定理的秘密：反機率雖然很有用，但要算反機率必須要先估計先驗機率。然而先驗機率不是唯一存在的客觀事實，它的估計必須要仰賴專業判斷。唯有基於經驗、理論、脈絡等專業資訊估計出來的先驗機率才能讓貝氏定理算出精確的反機率。