字體:小 中 大
字體:小 中 大 |
|
|
|
| 2013/12/15 22:31:33瀏覽2716|回應1|推薦7 | |
這篇是回覆http://blog.udn.com/ivan5chess/1750592提出的問題的解答 剛好有板友問到平行四邊形數目的部分,決定打一下也當作記錄下來^^
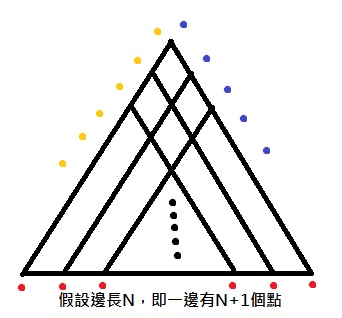
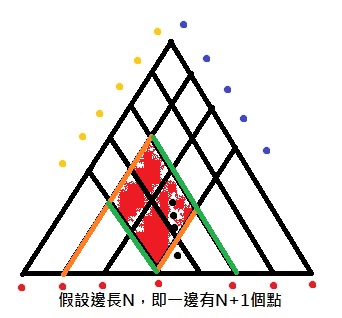
如圖,一個正三角形可以分成三個邊的方向(黃、藍、紅),若邊長是N,則邊上就會有N+1個點。 接著觀察一下,任意一個四邊形,可以看成是兩組平行的邊組成,如圖:
這兩組平行的邊延伸,都會落在紅邊的點上(因為平行四邊形的方向),反過來看,也就是說我們只要在紅邊上任取四個點,讓左兩個點延伸,右兩個點延伸,就可以組出一個平行四邊形(方向和上圖一樣) 所以方法數是C(n+1)取4 但是有一個情況要另外算,如圖:
當平行四邊形有一個點是落在紅邊上的時候,兩組平行邊延伸後,剛好會有一個點是重疊的,也就是說這些點剛好落在紅邊上的平行四邊形可以看成:在紅邊上任取三個點,左邊和中間的點延伸,再把中間和右邊的點往另一方向延伸 所以方法數是C(n+1)取3
綜合以上,可以得到像上圖平行四邊形方向的平行四邊形數目共有[C(n+1)取3]+[C(n+1)取4] = [C(n+2)取4],也就是說若要算出所有的平行四邊形數量,另外兩個方向的平行四邊形也考慮進去即可(數目和算法是一樣的) 所以答案是[C(n+2)取4] x3]
發現這樣打下來,加上畫圖,也花了好多時間阿(汗) |
|
| ( 知識學習|科學百科 ) |