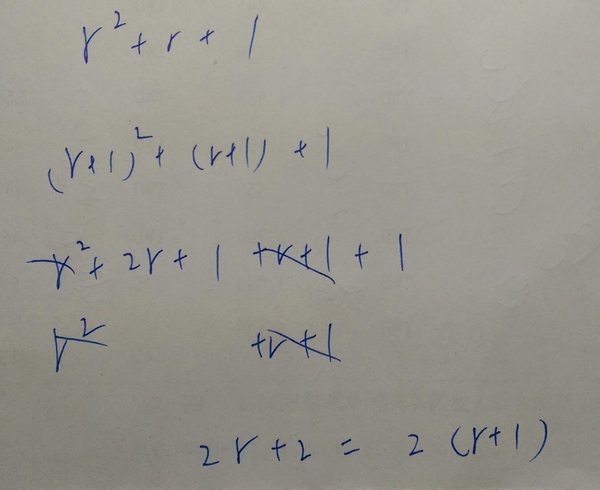國小簡單謎題(解答)兼憶往事及略述等差級數 

國小簡單謎題(繼續玩)    

本文是根據與女友專屬的芯闇~* 的討論串整理而成。

討論內容是哪些數字可以是等差級數的和，這部分已經解決。至於那些數字可以是等比級數的和還在思考中。

(1)可為等差級數和的數字的決戰前推導

我想到一些點可以討論。哪些數字可以是等差級數或是等比級數的和，當然等差級數的數量必須大於等於三(n>=3)。這些數字會有什麼特性？可能還是要從公式下手。 前提是級數的這些數字都是正整數，如果可用分數應該每個數字都可以了？  如果等差級數是三個數字：a, a+r, a+2r。和是3a+3r，所以和一定是3的倍數。 上底加下底乘高除以二的公式對這個問題好像沒什麼幫助。改用逐項列舉後，等差級數的和，等於na+(0+1+2+3+.....+n-1)r=na+(n(n-1)/2)r 。由於n,n-1,必定有一個是偶數，所以 (n(n-1)/2會是整數。 在a,r都是正整數的狀態下，可以確定不是每個數字都可以是等差級數的和。7明顯就不行。是不是質數都不行呢？ 上底加下底乘高除以二。

(2)等差級數和是否可為質數？

質數就不能分解成其他數字的乘積。 用我上面的式子，na+(n(n-1)/2)r=n(a+(n-1)/2)r)，除非(a+(n-1)/2)r)=1，但在a,n,r皆為正整數的情形下是不成立的，所以最少會是兩個數字的乘積，質數確定out！。 等差級數也必須排除公差為0的情況。上底加下底乘高除以二。(a+a+(n-1)r)n/2。所以我的寫法只是公式的另一種表達方式。好像錯了。我再想想 。 嗯。沒錯。等差級數在公差不為0且n大於等於3的情形下，其和不為質數。推論過程還要想想。

等差級數和的公式為(a+a+(n-1)r)n/2  n(a+(n-1)/2)r)  

n為偶數的情況下，因n大於等於3，n本身必定就不是質數。n為偶數的情況要再想想。 n為偶數的情況下，因n大於等於3，n本身必定就不是質數，且為2乘上某數P。n(a+(n-1)/2)r)=2P(a+(2P-1)/2)r)=P(2a+(2P-1)r)所以必定不是質數。

n為奇數的情況下，(n-1)/2為正整數，所以(a+(n-1)/2)r)為一正整數S，所以和為nxS，必定不是質數。  

(3)討論

7、5、3、1、-1、-3、-5 等差數列，合為質數，前提是必須是正整數。負數一定要扣掉的，不然討論就沒意義了，每個數都有辦法(應該吧 。 0也不能算，否則n大於等於3，這個前提就必須修改了。我想想。等差級數可以考慮0的狀況嗎？ 應該可以，似乎沒有造成任何數值都可以作為等差級數之和的狀況。等比級數絕對可ˇ以ˇ考ˇ慮ˇ0的狀況，不過結果只有一種........

(4)等差級數和為偶數時的推導

是不是所有偶數都可以是在所述前提下的等差級數的和？ 2,4,6太小了，因為n大於等於3，不考慮。從8開始想好了。  6其實可以，1,2,3，8反而不行......

 (a+a+(n-1)r)n/2=8 ，16=n(2a+(n-1)r)  n最少必須為4, 故(2a+(n-1)r)=4,在前提下，假設r=1,n=4,a不為正整數且小於1，故完全無解。

說 A A+R A+2R 合為3A+3R，所以三個等差數合最小為6。 四個數的話4A+6R所以最小是10。 8當然不行。 那10以上的偶數都可以是等差級數在前提下的和嗎？

三個數，即n=3時，和為 3(a+r),，3的倍數的偶數都可以

四個數，即n=4，和為2(2a+3r)。2(2a+3r),3-2=1,2a+3r可表示任何大於6的數字，所以任何數都可以，得證。

以三個等差數的合來說就是3a+3r，a、r都至少為1，也就是6、9、12、15...... 四個等差數的合是4a+6r，a、r至少為1，也就是10、14、16、18、20...... 14以上的偶數都可以是4個等差數的合，12可以是三個等差數的合，10可以是四個等差數的合。 所以10以上的偶數的確可以是等差數的合。

漂亮，偶數解決了。奇數再來玩。

(5)等差級數和為奇數時的擊倒前討論

n為偶數不可能和為奇數，n必須是奇數。3的你說了，來看5的，5a+10r=5(a+2r) 所以n=5時，在a,r合乎前提下，5的倍數都可。

所以6以上的3個倍數都可以是等差數的合。 四個等差數一定是偶數所以不用看四。 五個等差數為5a+10r，也就是15以上5的倍數。

數字有六個時...6a+15r，21、27、36......

七個時...7a+21r，28以上7的倍數。  n=7,7a+21r=7(a+3r)

六個數的合可能為奇數。 對耶 。 1+2+3+4+5+6=21。

(6)等差級數和為奇數時的推導

 3（2a+5r），3的7x、（7+2）X、（7+5）X倍數。 也就是21、27、36的倍數。來找規律好了。

n=3,3(a+r)

n=4,2(2a+3r)

n=5,5(a+2r)

n=6,3(2a+5r)

n=7,7(a+3r)

偶數自成一個規律，奇數另成一個規律。

n=4,2(2a+3r)

n=6,3(2a+5r)

 n=8, 4（2a+7r）

 n=3,3(a+r)

n=5,5(a+2r)

n=7,7(a+3r)

應該能解，看是不是所有奇數除了質數以外都可為其和。

當n為偶數設為2k,其等差級數和的通式為k(2a+(2k-1)r)。

當n為奇數設為2k+1,其等差級數和的通式為(2k+1)(a+kr)。

當n為偶數設為2k,其等差級數和的通式為k(2a+(2k-1)r)。k為奇數且r為奇數時，a可為偶數或奇數，其和為奇數。 柒七肆拾玖 由於2a必為偶數不影響和為奇數或偶數的結果，將2a刪去看是否有新發現。k(2k-1)r。可知r必然不為偶數。由於r確定其影響，將r刪去，再看。 k(2k-1) 乘開。k(2k-1)=2k^2-k 。看不出效用，再想想。

3x5,5x9,7X13 應該不是所有奇數都可以當等差級數的和，就算不是質數也不行。找到一個反例就可以證明了。 由於不是質數必定為兩個數字以上的乘積。當n為奇數設為2k+1,其等差級數和的通式為(2k+1)(a+kr)。

(2k+1)可為任意奇數

(a+kr)可為任何大於2k的奇數

故(2k+1)(a+kr)可以是任意奇數。

(7)可為等比級數和的數字的討論

等比級數的數量則大於等於2，等比級數的n(數量)還是必須大於等於三，討論才有意義。不然，1,(和減1)，每個數字都可以是等比級數的和了。在n大於等於3的前提下，等比級數的和好像還是可以是質數，7=1+2+4 。喔。還必須排除公比等於1的情況，不然11=1+1+1+1+1+1+1+1+1+1+1 柒七肆拾玖 等比級數的和應該還是要從公式下手，不過由於有次方數，一時也不知道怎麼做，就先放著了。突然想到，照我上面的說法，等比數列只有兩個數字時，和為任何數字都可以。那我的文章怎麼沒算到這個，78=1+77 。想通了。再補。原來是跟另外一個項目整除了！ r^n-1=(r-1)(r^n-1+r^n-2+.....+r+1)，如果n=2, a(r+1)=78, n=3,a(r^2+r+1)=78 。

n>=3,公比r>=2,所以和最小是1+2+4=7。

2+4+8=14 是 7的倍數。對。由此來看，只要確定某數是等比級數和，其倍數必然是。 所以只需考慮a=1的情況，a=2只是其兩倍。

是不是所有大於7的質數都可以是等比級數的和，嗯，不是，11就不是。不過有可能是因為11太小，畢竟我們的前提是n>=3。

不是。 23、29也不是。 7、13、21、31...... 2x3+1、3x4+1、4x5+1、5x6+1...... 想了一下，才知道你的算法，嗯，是針對n=3的狀況 公式是 a(r^n-1)/r-1,a=1,r=2的狀況，其和是2^n-1。等比級數的和跟等差級數和比起來，較為稀疏，不過是想當然的。有個難題，是否有一數，比這數大的任何質數皆可為等比級數的和。

 n=3的狀況有個規律，7,13,21,31。差距依序是 6,8,10，是個等差級數

 n=3 7、13、21、31、43、57、73、91、111

n=4 15、40、85、156、269

n=5 31、131、341、781

n=6 63、404、1365 其中只有7、13、31、43、73、131是質數。

從你給的數字結果來看，似乎只需考慮n為奇數或是質數的狀況，偶數看來其和都不會是質數。不對！269是質數啊~~~那還是沒有頭緒，不能省略n為偶數的情形。