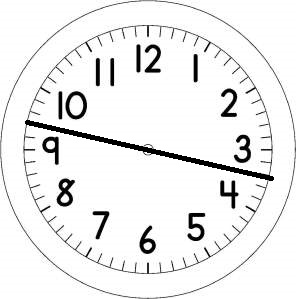
有一時鐘面如下，請試著將它分成幾個部份，每個部份的數字總和會相等。

試著解解看吧！

解答：這題是改編自小時候看的謎題集，作者是多湖輝，那本書可是我當時的武林秘笈，著實讓我風光了一陣子。

題目說，請試著將它分成幾個部份，每個部份的數字總和會相等。由於沒有限定是幾部份，試著解解看時，我們可以先嘗試分成兩部份，由於總共有12個數字，我們可以每部份包含6個數字，在我們試著將時鐘面切成兩半幾次後，我們發現從9,10中間切向3,4中間，所分成的兩部份，一是10,11,12,1,2,3，一是4,5,6,7,8,9，兩部份的合都是39，於是我們就得到了第一個答案。

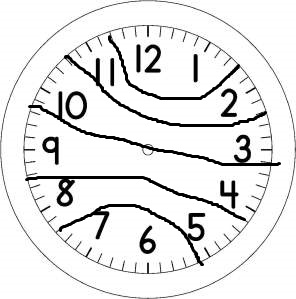
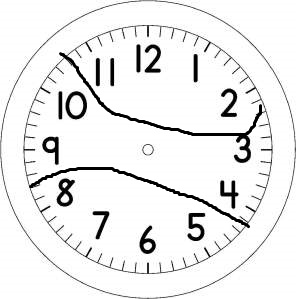
國小三年級時，老師曾多次讓我上台講述我從武林秘笈中讀來的謎題，讓同學解答。大部分的謎題都沒人能解答，大部分的同學也從沒解答出任何題目。但這一題，當初的題目是分成6個部分，某位同學的的確確實實在在的解答出來，那時我覺得他真是聰明，現在回頭看這題目，比起其他題目，難度算較低的，但國小三年級就能解答出來，我這位同學也算早慧了。曾在網路上搜尋過幾位同學的名字，不過沒有赫赫有名的人物或事蹟，或許是他們改名或是出國用外國名字，不過這算是太過善意的揣測了。

接下來我要用比較數學的方式解答這個題目。

時鐘上有12個數字，依大小依次是，1,2,3,4,5,6,7,8,9,1,0,11,12。注意到什麼了嗎？這是個等差數列，每個數字比前面多加個1。大家或許還記得等差級數的公式背法：

上底加下底乘高除以二。上底就是第一個數字，下底就是最後一個數字，高就是總共有幾個數字。

這個公式很好記，因為是從梯形面積算法直接套用上去，也沒有太難記的算法。

相傳等差級數的公式的由來，是某位數學家小時候的發明，那時他才國小一二年級，依現在的算法的話，那時他的老師因為想偷懶就叫學生算數學，從1加2加3一直加到100，想說這樣可以偷懶一會，可沒多久，這位以後的數學家就把答案算出來了。運用的就是等差級數的公式，想來我那位早慧的同學早生個幾世代或許有機會發展出這個公式吧。

等差級數公式： 上底加下底乘高除以二。上底就是第一個數字，下底就是最後一個數字，高就是總共有幾個數字。

時鐘上有12個數字，依大小依次是，1,2,3,4,5,6,7,8,9,1,0,11,12。

所以就是(1+12)X12/2。換個方式想的話，就是有6組相加為13的兩個數字，分別是1跟12，2跟11，3跟10，4跟9，5跟8，6跟7。

6=3X2

所以我們可以把鐘面分成6個總和相等的部份，也可以分成3個相等的部份，以及2個相等的部份。

分成6個總和相等的部份

分成3個總和相等的部份

分成2個總和相等的部份