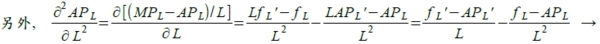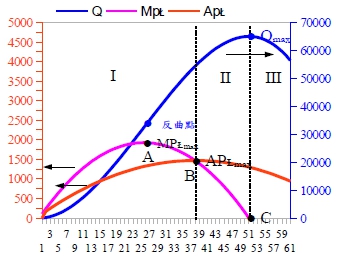
生產: 凡能創造或產生效用的經濟活動便是,包括財貨的創造與勞務的提供。

生產要素:生產者從事生產活動,所必需憑藉的各項投入: 勞動Labor, 土地, 資本(Capital, K), 技術technology, 管理Management....。

長短期生產過程區別: 短期--固定生產要素和變動生產要素, 長期--生產要素皆可變動。

生產函數與生產規模:

Q=f(X₁, X₂, …..)=f(L,K,t,M...)

生產函數: TP=Q=f(L,K,t,...), Q表示總產出或產量, L,K,t,..表示各種生產要素

生產關係: (1)短期生產函數TP=Q=f(L,K,t,...), 總產量(2)MPւ=fւ=ΔQ/ΔL, 邊際產量(3)APւ=Q/L, 平均產量。

1. 當總產量有Qₘₐₓ時, 必要條件有二: 其導數為零,即邊際產量MPւ=ΔQ/ΔL=fւ=0; 另外其二階導數小於零, ∂²f(L,K,t,...)/∂L²=fᴌᴌ(L,K,t,...)<0 (由圖中C點知邊際產量MPւ為零,對應的總產量即是Qₘₐₓ, 而且C點的斜率<0)

2. TP隨生產要素增加而增加, 其增加速度先遞增而後遞減。即邊際產量MPւ先增後減(邊際產量的斜率由正轉負),在A點出現極大值,因此∂MPւ/∂L=∂fւ/∂L= fււ=0, 對應在TP曲線上是反曲點。

3. 平均產量APւ與邊際產量MPւ的關係: 由圖中B點是APւ極大值, 且MPւ與APւ兩曲線交於B點;因B點是APւ極大值,所以APւ其導數為零:

dAPւ/dL= d(Q/L)/dL=[(LdQ-QdL)/L²]dL=1/L(dQ/dL- Q/L)=(MPւ-APւ)/L=0 ⸫ MPւ=APւ at B

在B點時,APւ是極大值 ⸫MPւ=APւ 且APւ=0 因此 fւ<0 即邊際產量的斜率小於零!

4. 觀察TP, APւ, MPւ三條曲線: TP由Qₘₐₓ之後開始遞減, APւ由B點之後開始遞減, MPւ則從A點之後開始遞減,0到A點稱為報酬遞增階段;超過A點稱為報酬遞減階段。

1. OB階段(區域I):未達到生產規模, TP處於上升階段,因為APւ還未達極大值。

2. BC階段(區域II最適生產階段):MPւ仍大於零直到MPւ=0, TP達到最高點時, 為最適之產量。當生產要素成本偏低,ex.空氣,產量趨近Qₘₐₓ,反之,則接近B點的產量。

3. >C階段(區域III):TP, APւ持續下降, 且MPւ<0, 此區域稱為不經濟區域。

Eulers theory:

1. 齊次homogeneous函數: 若z=f(x,y) → λᵏz=f(λx,λy) 表為k次齊次函數

ex. z=xy² 為 3 次齊次 → λ³z=(λx)(λy)²

ex. z=x-y 為 1 次齊次 → λz= λx-λy

2. 尤拉定理: 若已知z=f(x,y)為k次齊次函數,則λᵏz=f(λx,λy)

對λ微分 → kλᵏ⁻¹z=∂f(λx,λy)/∂(λx)∙∂(λx)/∂λ+∂f(λx,λy)/∂(λy)∙∂(λy)/∂λ

令λ=1 → kz=(∂z/∂x)∙x+(∂z/∂y)∙y

ex. 若已知Q=f(L,K)為一次齊次函數,則利用Eulers theory可得 Q=MPւ∙L+MPᴋ∙K

→ 1∙Q=(∂Q/∂L)∙L+(∂Q/∂K)∙K

等產量曲線:兩種生產要素生產相同產量的各種組合點連成的一條曲線。特性:

1. 它是一條負斜率的曲線，也就是說由左上往右下延伸的曲線。生產要素可以相互替代，但無法完全替代。

2. 有無限多條，越靠近原點的等產量曲線，其產量越小。

3. 任何兩條等產量曲線絕不相交。