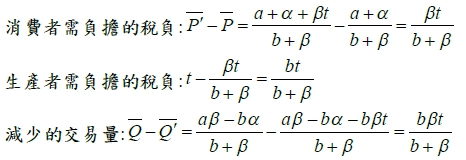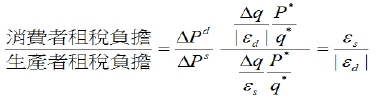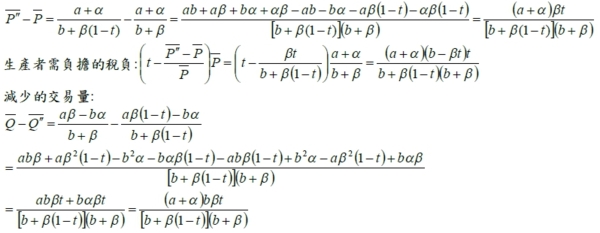字體:小 中 大
字體:小 中 大 |
|
|
|
| 2020/05/12 14:24:17瀏覽3094|回應0|推薦0 | |
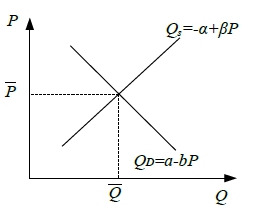
價格與交易量: 價格P為變數 需求函數:Qᴅ=a-bP, a, b>0 供給函數:Qs=-α+βP, α, β>0 求均衡價格P , 均衡交易量Q Qᴅ=a-bP=-α+βP=Qs → (b+β)P=a+α --> P=(a+α)/(b+β).....(1), Q=a-b∙(a+α)/(b+β)=(aβ-bα)/(b+β).....(2) only if b+β≠0
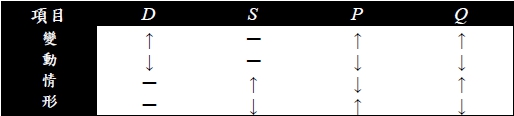
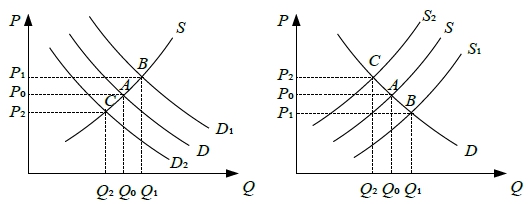
需求或供給發生變動:
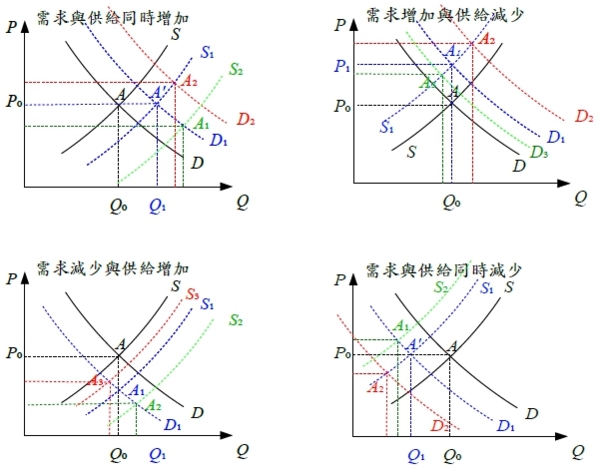
需求與供給同時變動:
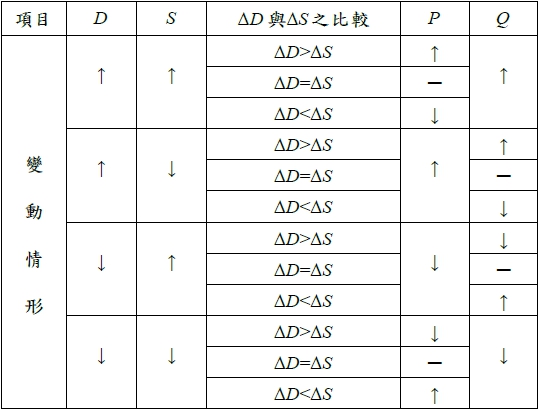
供需變動對均衡價格及交易量的影響:
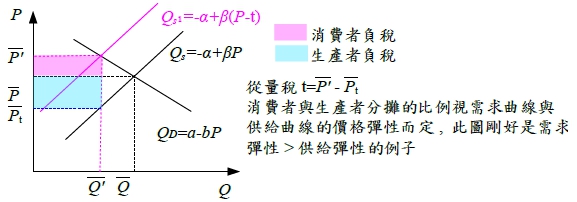
稅負對於供需之影響: 貨物稅: 分從量稅和從價稅 (a) 從量稅:每單位課徵t元, 即供給函數改變為: Qs=-α+β(P-t), α, β, t>0 求均衡價格, 均衡交易量 Qᴅ=a-bP=-α+β(P-t)=Qs → (b+β)P=a+α+βt --> P=(a+α+βt)/(b+β).....(3), Q=a-b∙(a+α+βt)/(b+β)=(aβ-bα-bβt)/(b+β).....(4) 若與課稅前之均衡價格P=(a+α)/(b+β).....(1)及均衡交易量Q=(aβ-bα)/(b+β).....(2)比較:
需求彈性及供應彈性也要看。簡單而言﹕ ex. 政府為了顧及人民的健康,想要人民減少吸菸次數和數量。假設對香菸的反需求函數( inverse demand function )可表示為 p=40 – 3q ,反供給函數( inverse supply function )可表示為 p=20+2q 。假設政府開始對香菸供應商課徵每單位香菸 10 元的稅,則: (1) 此時稅後均衡價格為何? (2) 消費者每單位香菸多付多少錢? (3) 這項租税政策對減少人民吸菸量的效果大小,與需求彈性有何關係? [解答] 以反需求與反供給函數計算原均衡為Pd= 40 - 3q = 20 + 2q = Ps,可求得均衡價格P*= 28 、均衡數量q*= 4 (1) 而對廠商課徵從量稅額後,新均衡為 Pd= 40 - 3q = 20 + 2q + 10 = Ps+τ,可稅後數量q’= 2 (2) 消費者支付的價格為 Pd= 40 - 3 x 2 = 34 、生產者收取的價格為Ps= 20 + 2 x 2 = 24 。 (3) 已知需求彈性|εd|=|∆q∙P*/(∆Pd∙q*)|、供給彈性εs=∆q∙P*/(∆Pѕ∙q*),故
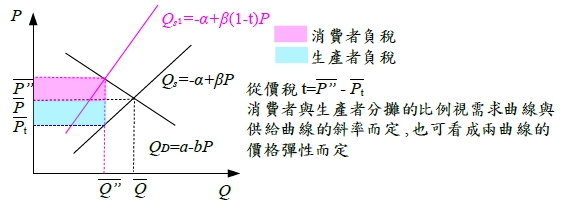
,表示租稅負擔與供需彈性的「反比」的關係。以本題為例,需求彈性|εd|=7/3、供給彈性εs=7/2,故(消費者租稅負擔)/(生產者租稅負擔)=εs/|εd|=3/2,表示 10 元的從量稅中,消費者將負擔 3/5 ,生產者負擔 2/5 ,則消費者面對的稅後價格為Pd=28+⅗(10)=34 (b) 從價稅: 每單位課徵特定百分比t 的稅負, 即供給函數改變為:Qs=-α+β(1-t)P, α, β>0, 1>t>0求均衡價格, 均衡交易量 Qᴅ=a-bP=-α+β(1-t)P=Qs → [b+β(1-t)]P=a+α --> P”=(a+α)/[b+β(1-t)].....(5), Q”=a-b∙(a+α)/[b+β(1-t)]=[aβ(1-t)-bα]/[b+β(1-t)].....(6) 若與課稅前之均衡價格P=(a+α)/(b+β).....(1)及均衡交易量Q=(aβ-bα)/(b+β).....(2)比較: 消費者需負擔的稅負:
|
|
| ( 知識學習|商業管理 ) |