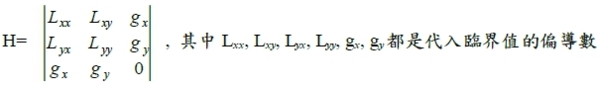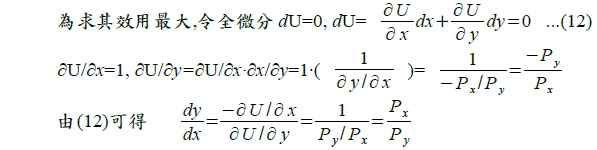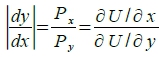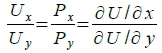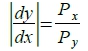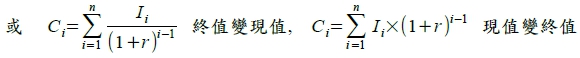字體:小 中 大
字體:小 中 大 |
|
|
|
| 2020/05/14 14:33:11瀏覽1807|回應0|推薦0 | |
optimization最適化: 在經濟上, ex. 最大效用的購買組合(支出限制下)、最小成本的生產組合(預定產量水準下)、最大利潤、最大淨投報率。以數學角度看最適化, 即是求(絕對或相對)極大或極小值, 先熟悉一些極值定理: 極值的一階導函數檢定法: 設函數f在包含c之某一區間內連續,且c為此區間內之一臨界數,則(1)若由點c之左側至右側,導數f由正變負,則f(c)為f之相對極大值 (2)若由點c之左側至右側,導數f由負變正,則f(c)為f之相對極小值 (3)若導數f於點c之二側的符號相同,則f(c)不為f之相對極值。 極值的二階導函數檢定法: 設f(c)=0, 且f”(c)存在,則 (1)若f”(c)>0, 則f(c)為相對極小值 (2) 若f”(c)<0, 則f(c)為相對極大值 (3)若f”(c)=0, 則f(c)為反曲點 兩變數函數之極值的檢定與求法: 設f(x,y)為一兩變數函數, 且x=a, y=b之點能使fₓ(a,b)=0, fy(a,b)=0, 若令△=fₓₓ(a,b)fyy(a,b)-[fₓy(a,b)]² 則 (1)若△>0, 且fₓₓ(a,b)<0, 則f(a,b)為f之相對極大值 (2) 若△>0, 且fₓₓ(a,b)>0, 則f(a,b)為f之相對極小值 (3)若△<0, 則f(a,b)既非相對極大值,也非相對極小值 (4)若△=0, 則必須利用其他方法才能判斷f(a,b)是否為相對極值 以數學角度來看,所謂限制條件之極值問題,乃是求一函數f(x,y)的極值,而(x,y)須滿足某一方程式g(x,y)=0,此g(x,y)=0稱為限制條件式,而f(x,y)稱為目標函數。解決這種問題的方法之一是: 將限制條件式g(x,y)=0,解出y為x之函數,再代入目標函數f, 使f變成x之單變數函數,再利用上述檢定法求解。 ex. 設某廠商生產A, B兩種產品, x, y分別表示A,B的產量, 其價格分別為Pᴀ=37.5, Pᴃ=15, 如其總成本函數為C(x,y)=2x²+xy+2y² 試求利潤極大時, A,B的產量各為多少?利潤有多少? PA=37.5, PB=15, C(x,y)=2x²+xy+2y² 利潤π=R-C=Pᴀ∙x+Pᴃ∙y-C(x,y)=37.5x+15y-(2x²+xy+2y²)
πxx=-4<0, πyy=-4<0, πxy=-1 △=πxxπyy-πxy2=16-1=15>0有相對極大值 π(9,1.5)=37.5*9+15*1.5-(2*92+9*1.5+2*1.52)=337.5+22.5-(162+13.5+4.5) =360-180=180萬 當限制條件g(x,y)=0為一隱函數,無法求得y為x之函數,我們可以引進lagrange multiplier, λ 將目標函數f和限制條件式g(x,y)=0連結,形成一新函數,稱為Lagrangian function : L(x,y,λ)=f(x,y)+ λg(x,y) 以上函數的極大值或極小值的必要條件為: L對三變數x, y, λ的一階偏導數為零, 亦即Lₓ(x,y,λ)=fₓ(x,y)+ λgₓ(x,y)=0, Ly(x,y,λ)=fy(x,y)+ λgy(x,y), Lλ(x,y,λ)=g(x,y)=0 聯立求解前三式可得x, y, λ之值, 而且此組臨界值又滿足其中 Lλ(x,y,λ)=g(x,y)=0限制條件式, 所以L(x,y,λ)的極值一定與目標函數f(x,y)的極值相等。 另外其充分條件:
(1)若H>0, L(x,y,λ) 函數值為f之相對極大值 (2)若H<0, L(x,y,λ) 函數值為f之相對極小值 ex. 在x+2y=10之限制下, 求f(x,y)=x2+y2+10之極值。 constrained equation x+2y=10 → x+2y-10=0 f(x,y)=x2+y2+10 L(λ, x, y)=f(x,y)-λ(x+2y-10)= x2+y2+10-λ(x+2y-10) Partial differentiating x, y, and λ respectively dL/dx=2x-λ=0 dL/dy=2y-2λ=0 dL/dλ= x+2y-10=0, get λ=4, x=2, y=4 ∴extreme value=f(2,4)=4+16+10=30 限制條件下的最適化: 靜態分析、比較靜態分析、動態分析 1. 靜態分析(消費者行為分析) 支出受限制下,求效用最大 支出的限制條件: E=x∙Pₓ+y∙Py ...(9) E表示消費者的支出, x和y各為其財貨的數量, Pₓ和Py各為其財貨的價格 效用函數: U=U(x,y) ...(10) 解一: E₀=x∙Pₓ+y∙Py ...(9) 則 y= E₀/Py- x∙Pₓ/Py ….(11) ps. E₀, Pₓ和Py視為常數 代入效用函數: U=U(x,y)=U(x, E₀/Py- x∙Pₓ/Py)
分析→效用極大化的必要條件:
當x對y 邊際替代率dy/dx等於兩種財貨的價格比Pₓ/Py ,並且等於兩種財貨的邊際效用比。 解二: 用λ將(9), (10)連結起來 L(x,y,λ)=U(x,y)-λ(E₀-x∙Pₓ-y∙Py) → 分別對x, y, λ求偏導數 ∂L/∂x=Uₓ+λPₓ=0 ...(13), ∂L/∂y=Uy+λPy=0 ...(14), ∂L/∂λ= E₀-x∙Pₓ-y∙Py=0 ...(15) 由(13), (14)相除可得
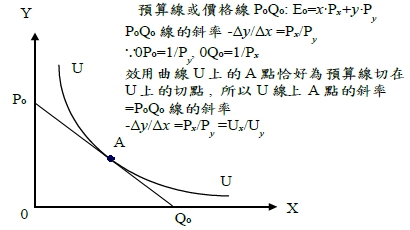
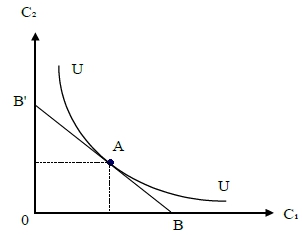
當x財貨的邊際效用與y財貨的邊際效用之比值, 等於x財貨的價格與y財貨的價格之比值,其效用為極大 效用受限制下,求支出最小 效用的限制條件: U=U(x,y)=U₀ 支出函數: E=x∙Pₓ+y∙Py 解一: 求支出最小, 表示dE=0 → dx∙Pₓ+dy∙Py=0 → dy/dx=-Pₓ/Py → 也就是支出函數有極值的條件: 支出函數(預算線或價格線)的曲線斜率的絕對值\(亦即x對y 邊際替代率)等於x財貨的價格與y財貨的價格之比值。 以數學來看, E=x∙Pₓ+y∙Py是一條具有負斜率的直線, 其x截距0Q₀=1/Pₓ,y截距0P₀=1/Py, 此線代表支出函數,須在固定的效用限制下,得到最小的支出,換成數學語言,兩個函數必須有交集;兩個方程式須有共同解才成立,圖形上要有交點或切點,才是所求的解,因此上述條件也要滿足效用的限制: U(x,y)=U₀ → dU=Uₓdx+Uydy=0 → dy/dx=-Uₓ/Uy ⸫ dy/dx=-Pₓ/Py=-Uₓ/Uy
2. 動態分析: 以兩個時點(現在及未來)的消費型態為例 現在消費C₁(現期), 及未來消費C₂(下一期),並假設現期所得I₁及未來所得I₂,由消費者決定在哪一期消費的效用最大? C₁, C₂與I₁, I₂的關係: C₁=I₁+I₂/(1+r), C₂=I₁(1+r)+I₂ 註: r為利率 現值與終值轉換的概念
若將期數擴展至n期,則 C₁=I₁+I₂/(1+r)+I₃/(1+r)²+...+Iₙ/(1+r)n⁻¹, Cₙ= I₁(1+r)n⁻¹+I₂(1+r)n⁻²+...+Iₙ₋₁(1+r)+Iₙ
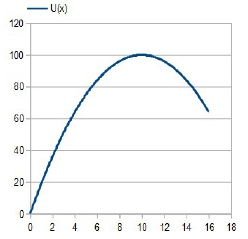
無限制條件下的最適化: 例如自由財的攝取, ex. 溪水、空氣 ex. 享用免費餐點,其效用函數: U(x)=-x²+20x dU(x)/dx=-2x+20=0, d²U/dx²=-2<0 表示x=10時,有最大效用U=100
ex. 某廠商生產兩種產品x和y, 其成本函數: C(x,y)=0.04x²+0.01xy+0.01y²+4x+2y+500 設此廠商以每單位15元的x及9元的y銷售,試求x, y產量多少時利潤最大? 利潤π(x,y)=15x+9y-C(x,y)= -0.04x²-0.01xy-0.01y²+11x+7y-500 一階導數: dπ=πₓdx+πydy=(-0.08x-0.01y+11)dx+(-0.01x-0.02y+7)dy 二階導數: d²π=(-0.08dx-0.01dy)dx+(-0.01dx-0.02dy)dy=-0.08dx²-0.02dxdy-0.02dy² 一階條件: πₓ=πy=0, -0.08x-0.01y+11=-0.01x-0.02y+7=0 → x=100, y=300 二階條件: πₓₓ=-0.08<0, πyy=-0.02<0, πₓy=-0.02 → △= πₓₓ∙ πyy- πₓy²=(-0.08)(-0.02)-(-0.02)²>0 所以當 x=100, y=300, 利潤為1100是極大值 |
|
| ( 知識學習|商業管理 ) |



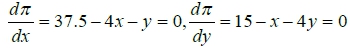 → x
→ x