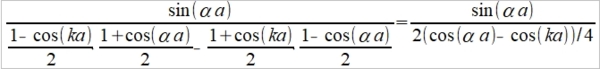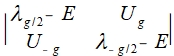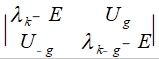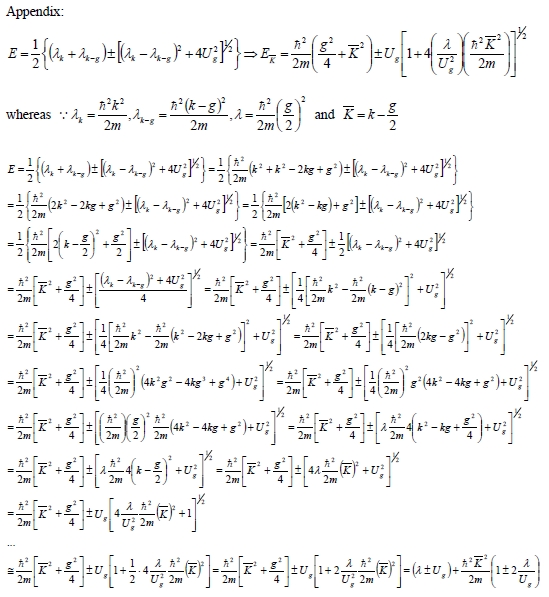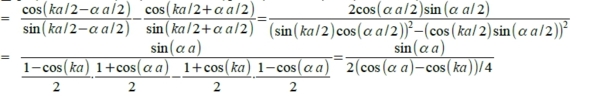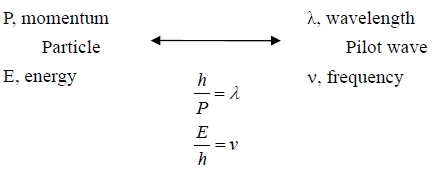字體：小中大

能帶理論

2017/12/13 21:52:51瀏覽1604｜回應0｜推薦0

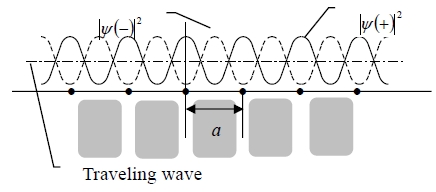
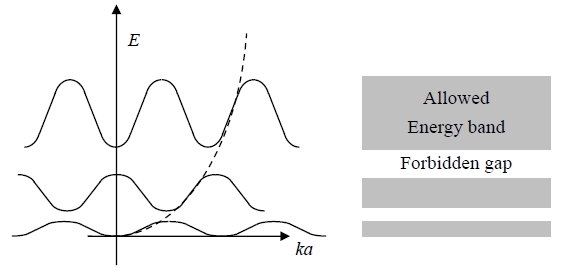
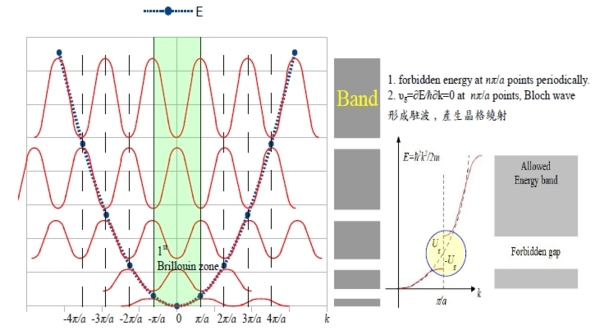
Chap. 7 Energy Gap

Two different standing waves, k=±π/a

ψ(+)=2cos(πx/a), ψ(-)=2isin(πx/a) in 1-D

Charge probability density, ρ(+)=|ψ(+)|²  cos²(πx/a) at x=0, a, 2a, 3a…能量最低

ρ(-)=|ψ(-)|²  sin²(πx/a) at x= a/2, 3a/2, 5a/2…能量較高

Normalized standing wave:

∫|ψ(+)|²dx=1 → A²∫₀^acos²(πx/a)dx=1 → A²a/π∫₀^πcos²ydy=1 → A²a/π(y/2+sin2y/4)|₀^π=1

→ A²a/2=1, A=(2/a)^1/2 ⸫ ψ(+)=(2/a)^1/2cos(πx/a)

同理, ψ(-)=(2/a)^1/2sin(πx/a)

potential energy, U(x)=U₀cos(2πx/a) → U(+)=∫ψ*(+)Uψ(+)dx, U(-)=∫ψ*(-)Uψ(-)dx

E_g=U(-) - U(+)=U₀

Bloch theorem

Hψₙ=Eψₙ, (ℏ²k²/2m+U)ψₙ=Eψₙ

⸪晶格為週期性排列→ ψₙ亦為週期性函數

the solution of Schrödinger equation for a periodic potential,

ψ_k₍_r₎=e^ik^∙^r∙u_k₍_r₎ where u_k₍_r₎=u_k₍_r₊_T₎ T: translation vector

→ ψ_k₍_r₎=ψ_k₍_r₊_T₎ 表示相位相同即起始條件一樣

Free electron model: ψ_k₍_r₎=e^ik^∙^r, 平面波,自由電子沒有位能存在

Nearly free electron model: ψ_k₍_r₎=e^ik^∙^r∙u_k₍_r₎ Bloch function(描述理想晶體時)

Kronig-Penny model(1-D)

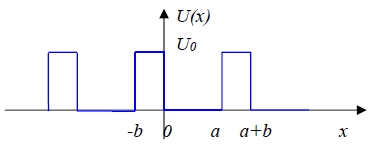
(-ℏ²/2m)d²ψ∕dx²+Uψ=Eψ, H=(-ℏ²/2m)d²/dx²+U

in the region 0<x<a, U=0

d²ψ∕dx²+2mEψ/ℏ²=0, K²= 2mE/ℏ²

ψ₁(x)=Ae^iKx+Be^-iKx

in the region a<x<a+b, U=U₀

d²ψ∕dx²-2m(U₀-E)ψ/ℏ²=0, let Q²= 2m(U₀-E)/ℏ²

ψ₂(x)=Ce^Qx+De^-Qx

Boundary conditions: ψ₁(a)=ψ₂(a) and dψ₁/dx|_x=a=dψ₂/dx|_x=a when x=a

→ Ae^iKa+Be^-iKa=Ce^Qa+De^-Qa, iKAe^iKa-iKBe^-iKa=QCe^Qa-QDe^-Qa 解C, D

C=e^-Qa/2Q[Q(Ae^iKa+Be^-iKa)+(iKAe^iKa-iKBe^-iKa)], D=e^Qa/2Q[Q(Ae^iKa+Be^-iKa)-(iKAe^iKa-iKBe^-iKa)]

⸫ ψ₁(x)=Ae^iKx+Be^-iKx,

ψ₂(x)=e^Q⁽^x^-a⁾/2Q[Q(Ae^iKa+Be^-iKa)+(iKAe^iKa-iKBe^-iKa)]+e^-Q⁽^x-a⁾/2Q[Q(Ae^iKa+Be^-iKa)-(iKAe^iKa-iKBe^-iKa)]代入 bloch function

ψ(x+a+b)=u(x+a+b)e^ik⁽^x+a+b⁾=u(x)e^ikxe^ik⁽^a+b⁾=ψ(x)e^ik⁽^a+b⁾, 令x=0

ψ₂(a+b)=ψ₁(0)e^ik⁽^a+b⁾, and dψ₂(a+b)/dx=[dψ₁(0)/dx]e^ik⁽^a+b⁾ 將ψ₁, ψ₂代入解A, B

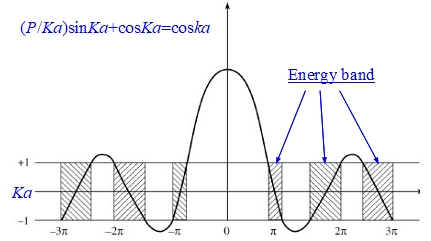
得 [(Q²-K²)/2QK](sinhQb)sinKa+(coshQb)cosKa=cosk(a+b)…(a),

Q²= 2m(U₀-E)/ℏ², K²= 2mE/ℏ², k=2π/λ

in the limiting case: b→0, U₀→ and define P=Q²ba/2 a finite quantity.

sinhQb=(e^Qb-e^-Qb)/2≈1/2[(1+Qb+Q²b²/2+...)-(1-Qb+Q²b²/2-...)]=Qb,

coshQb=(e^Qb+e^-Qb)/2≈1

(a)簡化為(Q/2K)QbsinKa+cosKa=coska ⸫ (P/Ka)sinKa+cosKa=coska

P0 coska=1 at the X points, ka=nπ, n=1, 2, 3,… k=nπ/a時發生不連續

ka=π, k=π/a → E=ℏ²k²/2m=ℏ²|π/a|²/2m=E_π_₁ , ℏ²|(π+∆)/a|²/2m=E_π_₂

Wave equation of electron in a periodic potential for a general crystal potential

U(r)=U(r+T) 3-D vs. U(x)=U(x+na) 1-D

U(x) can be expanded as a Fourier series in the reciprocal lattice.

U(x)=∑_GU_Ge^iGx=∑_G_>0U_G(e^iGx+e^-^iGx)=2∑_G_>0U_GcosGx代入Schrodinger equation

[P²/2m+U(x)]ψ(x)=Eψ(x), P=-ih(d/dx) → [(-ℏ²/2m)d²/dx²+U]ψ(x)=Eψ(x)…(b)

解ψ(x)=∑_kC(k)e^ikx, k=2nπ/L and U(x)=∑_GU_Ge^iGx代入(b)

[(-ℏ²/2m)d²∑_kC(k)e^ikx/dx²+∑_GU_Ge^iGx∑_kC(k)e^ikx=E∑_kC(k)e^ikx

→ (ℏ²k²/2m)∑_kC(k)e^ikx+∑_GU_Ge^iGx∑_kC(k)e^ikx=E∑_kC(k)e^ikx

→ (ℏ²k²/2m)∑_kC(k)e^ikx+∑_G∑_kU_GC(k)eⁱ⁽^G^+k⁾^x=E∑_kC(k)e^ikx

上式等號左邊第二項∑_G∑_kU_GC(k)eⁱ⁽^G^+k⁾^x, 將k 換成 k+G

→ ∑_G∑_kU_GC(k)eⁱ⁽^G^+k⁾^x=∑_G∑_kU_GC(k-G)eⁱ^k^x=∑_G∑_kU_GC(k-G)e^ikx

By equating the coefficient of e^ikx on both sides.

∑_k[(ℏ²k²/2m)C(k)+∑_GU_GC(k-G)]e^ikx=∑_kEC(k)e^ikx→ (ℏ²k²/2m)C(k)+∑_GU_GC(k-G)=EC(k)

⸫ (λₖ-E)C(k)+∑_GU_GC(k-G)=0…central equation, λₖ= ℏ²k²/2m

*只要C(k)存在,必有一C(k-G)存在

→ ψ(x)=∑_GC(k-G)eⁱ⁽^k-G⁾^x=∑_GC(k-G)e^-^iGxe^ikx= u_k(x)e^ikx, ∑_GC(k-G)e^-^iGx=u_k(x)

if u_k(x+T)=u_k(x)滿足bloch equation的要求

u_k(x+T)=∑_GC(k-G)e^-^iG⁽^x+T⁾=∑_GC(k-G)e^-^iGx∙e^-^iGT, G=2mπ/a, T=na ⸫GT=2mnπ

U(x)=∑_GU_Ge^iGx, G=2nπ/a

另類導出Kronig-Penney model solution:

U(x)=∑_GU(G)eⁱ^Gx=A∙a∙∑ₛδ(x-sa)

i.e. delta function ∫₀^ₐδ(x-sa)dx=1 → ∫₀^ₐδ(x-a)f(x)dx=f(a)

U(G)=1/a∫₀^ₐdxU(x)e^-i^Gx=1/a∫₀^ₐdxA∙a∙∑ₛδ(x-sa)e^-i^Gx=A∑ₛ∫₀^ₐδ(x-sa)e^-i^Gxdx=A∑ₛe^-i^G^s^a=A∑ₛe^-i2^π^ns

G=±2πn/a reciprocal vector, 某一個U_G對應一個s值, ⸫U_G= A 代入central eq.

→ (λ_k -E)C(k)+∑ₙAC(k-2πn/a)=0 define: f(k)=∑ₙC(k-2πn/a), and f(k)=f(k-2πn/a)

→ C(k)=-Af(k)/(λ_k -E)=-[(2mA/ℏ²)f(k)]/[k²-(2mE/ℏ²)] 代入 λ_k = ℏ²k²/2m

上式用k-2πn/a代換k

C(k-2πn/a)=-[(2mA/ℏ²)f(k-2πn/a)]/[(k-2πn/a)²-(2mE/ℏ²)]=-[(2mA/ℏ²)f(k)]/[(k-2πn/a)²-(2mE/ℏ²)]

→ ∑ₙC(k-2πn/a)=-(2mA/ℏ²)f(k)∑ₙ1/[(k-2πn/a)²-(2mE/ℏ²)]

→ - ℏ²/2mA=∑ₙ[(k-2πn/a)²-(2mE/ℏ²)]⁻¹ i.e. α²=2mE/ℏ²

→ - ℏ²/2mA=∑ₙ[(k-2πn/a)²-α²]⁻¹=∑ₙ[(k-2πn/a-α)(k-2πn/a+α)]⁻¹=∑ₙ(1/2α)[(k-2πn/a-α)⁻¹-(k-2πn/a +α)⁻¹]=∑ₙ(1/2α)[a/(ka-2πn-αa)-a/(ka-2πn+αa)]

→ - ℏ²/2mA=(a/4α)∑ₙ[1/(ka/2-αa/2-πn)-1/(ka/2+αa/2-πn)] i.e. cotx=∑ₙ1/(nπ±x)

∑ₙ[1/(ka/2-αa/2-πn)-1/(ka/2+αa/2-πn)]=cot(ka/2-αa/2)-cot(ka/2+αa/2)

=cos(ka/2-αa/2)/sin(ka/2-αa/2)-cos(ka/2+αa/2)/sin(ka/2+αa/2)

=2cos(αa/2)sin(αa/2)/[sin²(ka/2)cos²(αa/2)-cos²(ka/2)sin²(αa/2)]

=

→ - ℏ²/2mA=(a/4α)[2sinαa/(cosαa -coska)]=(a/2α)[sinαa/(cosαa -coska)]

→ - ℏ²α/maA=sinαa/(cosαa -coska)

→ coska=cosαa+(maA/ℏ²α)sinαa=cosαa+(P/αa)sinαa

→ coska=cosαa+(P/αa)sinαa P=ma²A/ℏ²

Ex: U(x)=U₂_π_/_aeⁱ²^πx^/^a+U_-₂_π_/_ae^-ⁱ²^πx^/^a=2U₀cos(2πx/a)=2Ucos(gx), U₂_π_/_a=U_-₂_π_/_a=U_g=U_-g=U₀

(λₖ-E)C(k)+∑_GU_GC(k-G)=0 → (λₖ-E)C(k)+U_gC(k-g)+U_-gC(k+g)=0

Approximation solution near a zone edge
1. At the zone edge
(λₖ-E)C(k)+∑_GU_GC(k-G)=0, k=g/2=π/a and λ_k =ℏ²k²/2m

ψ(x)=∑_GC(k-G)eⁱ⁽^k-G⁾^x≈C(k)e^ikx+C(k-g)eⁱ⁽^k-g⁾^x=C(g/2)e^igx^/2+C(-g/2)e^-^igx^/2

U(x)=∑_GU(G)eⁱ^Gx=U₂_π_/_aeⁱ²^πx^/^a+U_-₂_π_/_ae^-ⁱ²^πx^/^a=2U₀cos(2πx/a), when G=2π/a

as k=g/2, ⸪U_G1/G² →取C(k-g) and C(k+g)二項近似, 其餘忽略

→ (λₖ-E)C(k)+U_gC(k-g)+U_-gC(k+g)=0 → (λ_g_/2 -E)C(g/2)+U_gC(k-g)+U_-gC(k+g)=0

→ (λ_g_/2 -E)C(g/2)+U_gC(-g/2)+U_-gC(3g/2)=0 → (λ_g_/2 -E)C(g/2)+U_gC(-g/2)=0...(1)

as k=-g/2

→ (λₖ-E)C(k)+U_gC(k-g)+U_-gC(k+g)=0 → (λ_-_g_/2 -E)C(-g/2)+U_gC(-3g/2)+U_-gC(g/2)=0

→ (λ_-_g_/2 -E)C(-g/2)+U_-gC(g/2)=0

for non-trivial solution of C(k) → =0

→ E²-(λ_g_/2+λ_-_g_/2)E+λ_g_/2λ_-_g_/2-U_gU_-g=0

⸪ λ_k =ℏ²k²/2m → λ_g_/2= ℏ²(g/2)²/2m= ℏ²(-g/2)²/2m=λ_-_g_/2 and U_g=U_-g=U₀

⸫ (λ_g_/2-E)²-U_g²=0 → E=λ_g_/2±U_g=ℏ²(g/2)²/2m±U_g, for E(+)= λ_g_/2+U_g=ℏ²(g/2)²/2m+U_g

代入(1)式, [λ_g_/2 -E(+)]C(g/2)+U_gC(-g/2)=0 → C(g/2)/C(-g/2)=-U_g/[λ_g_/2 -E(+)]=+1

ψ(x)= C(g/2)e^igx^/2+C(-g/2)e^-^igx^/2=C(g/2)(e^igx^/2+e^-^igx^/2)=2C(g/2)cos(gx/2)=2C(g/2)cos(πx/a)

x=0, a, 2a,…|ψₖ₍₊₎|²  |cos(πx/a)|² 電子在晶格點上的機率最大,總能量也較低

for E(-)= λ_g_/2-U_g=ℏ²(g/2)²/2m-U_g→ [λ_g_/2 -E(-)]C(g/2)+U_gC(-g/2)=0 → C(g/2)/C(-g/2)=-U_g/[λ_g_/2 -E(-)]=-1

ψ(x)= C(g/2)e^igx^/2+C(-g/2)e^-^igx^/2=C(g/2)(e^igx^/2-e^-^igx^/2)=2C(g/2)sin(gx/2)=2C(g/2)sin(πx/a)

x=a/2, 3a/2,…|ψₖ₍₋₎|² = |2C(g/2)sin(πx/a)|²
1. If the wavevector k is very near the zone edge(k→g/2, but k≠g/2)
取前二項近似, C(k) and C(k-g)

ψ(x)=∑_GC(k-G)eⁱ⁽^k-G⁾^x≈C(k)e^ikx+C(k-g)eⁱ⁽^k-g⁾^x代入bloch equation

(λₖ-E)C(k)+∑_GU_GC(k-G)=0 → (λₖ-E)C(k)+U_gC(k-g)+U_-gC(k+g)=0 and (λₖ₋_g-E)C(k-g)+U_gC(k-2g)+U_-gC(k)=0 →取前二項近似, C(k) and C(k-g)

→ (λₖ-E)C(k)+U_gC(k-g)=0...(3), (λₖ₋_g-E)C(k-g)+U_-gC(k)=0...(4)

for non-trivial solution of C(k) → =0

→ E²-(λ_k+λ_k-_g)E+λ_kλ_k-_g-U_g²=0(⸪U_g=U_-g=U₀), E=½{(λ_k+λ_k-_g)±[(λ_k+λ_k-_g)²-4(λ_kλ_k-_g-U_g²)]^1/2}

→ E=½{(λ_k+λ_k-_g)±[(λ_k-λ_k-_g)²+4U_g²)]^1/2}, ⸪ λ_k=ℏ²k²/2m, λ_k-_g=ℏ²(k-g)²/2m, λ=ℏ²(g/2)²/2m

and let K=k-g/2 可以將解整理成E_K=(ℏ²/2m)(g²/4+K²)±U_g[1+4(λ/U_g²)(ℏ²K²/2m)]^1/2 i.e. λ_k+λ_k-_g=2λ+ ℏ²K²/2m, λ_k-λ_k-_g= ℏ²2Kg/2m

when k→g/2=π/a, 4(λ/U_g²)(ℏ²K²/2m)=(ℏ²Kg/2mU_g)²<<1 span="">

⸫ E_K(±)≈(ℏ²/2m)(g²/4+K²)±U_g[1+½∙4(λ/U_g²)(ℏ²K²/2m)]=(λ±U_g)+(ℏ²K²/2m)(1±2λ/U_g)
1. - 1. upper band, U_g<0, font="" face="Times New Roman, serif">E_K(-)=(λ-U_g)+(ℏ²K²/2m)(1-2λ/U_g)
    2. lower band ⸫ E_K(+)=(λ+U_g)+(ℏ²K²/2m)(1+2λ/U_g)
numbers of states in a band:

consider a linear crystal constructed of N primitive cells of lattice constant a

根據週期性條件U(sa)=U(sa+L), k=0, ±2π/L, ±4π/L,...Nπ/L, L=Na

[π/a-(-π/a)]/(2π/L)=Na/a=N, 在第一不連續中有N個states, 考慮spin每個state有兩個不同的spin(down and up), there are 2N independent states in each energy band→2N electrons
1. for alkali metals which have one valence electron per primitive cell. N cells → N valence electrons → the energy band is half-filled → metal
2. for Alkali earth metal: each primitive cell have two valence electrons → N cells → 2N valence electrons → band is filled up → insulators.
If the bonds are partly overlapped → semiconductors

For diamond, silicon and Ge: each primitive cell has 2 atoms, each atom has 4 valence electrons. N cells have 8N valence electrons

可填滿4個band,且無overlap現象, energy gap~kT→semiconductor

Appendix:

E=½{(λ_k+λ_k-_g)±[(λ_k-λ_k-_g)²+4U_g²)]^1/2}

→ E_K=(ℏ²/2m)(g²/4+K²)±U_g[1+4(λ/U_g²)(ℏ²K²/2m)]^1/2,

⸪ λ_k=ℏ²k²/2m, λ_k-_g=ℏ²(k-g)²/2m, λ=ℏ²(g/2)²/2m and let K=k-g/2

Quantum mechanics of electrons in crystal lattices R. De L. Kronig and William George Penney published: Proc. Roy. Soc. 03 Feb. 1931 vol. 130 Issue 814

Solutions of Kronig-Penney Models by the T-Matrix Method William J. Titus American Journal of Physics 41, 512 (1973)

Kronig-Penney model: electron in a periodic field of a crystal

I: d²ψ/dx²+(2mE/ℏ²)ψ(x)=0 α²=2mE/ℏ²

II: d²ψ/dx²+(2m/ℏ²)(E-V₀)ψ(x)=0 γ²=(2m/ℏ²)(V₀-E)

Bloch wave: ψ(x)=u(x)eⁱ^kx u(x): periodic function, different for various directions in crystal.

代入I, II方程式

d²ψ/dx²= d²(u(x)eⁱ^kx)/dx²=d/dx[(du/dx)eⁱ^kx+iku(x)eⁱ^kx]

=(d²u/dx²)eⁱ^kx+ik(du/dx)eⁱ^kx+ik[(du/dx)eⁱ^kx+iku(x)eⁱ^kx]=[(d²u/dx²)+2ik(du/dx)-k²u(x)]eⁱ^kx

⸫ I (d²u/dx²)+2ik(du/dx)-k²u(x)+α²u(x)=0 → D²u+2ikDu+(α²—k²)u=0 → D=-ik±iα

u(x)=(Aeⁱ^αx+Be⁻ⁱ^αx)e⁻ⁱ^kx

II (d²u/dx²)+2ik(du/dx)-k²u(x)-γ²u(x)=0 → D=-ik±γ

u(x)=(Ce^γ^x+De⁻^γ^x)e⁻ⁱ^kx

Schrödinger eq. -ℏ²/2m(d²ψ/dx²)+U(x)ψ(x)=Eψ(x)

potential in periodic crystal U(x+a)=U(x) a: lattice constant

expanding wave function and potential function by Fourier series

ψ(x)=∑ₖC(k)eⁱ^kx, U(x)=∑_GU(G)eⁱ^Gx

where G =2πn/a is the reciprocal lattice vector and

U(G)=U_G =1/a∫₀^ₐdxU(x)e^-i^Gx (7.69)

Because U(x) is real, it is easy to show that U_G* = U_-_G.

U_G* =[1/a∫₀^ₐdxU(x)e^-i^Gx]*=1/a∫₀^ₐdxU(x)eⁱ^Gx= 1/a∫₀^ₐdxU(x)e_-^i(-^G⁾^x= U_-_G (7.70)

We can use these plan waves as our basis, and therefore we can write any wavefunction in the following form

ψ(x)=∑ₖC(k)eⁱ^kx (7.71), C(k)=1/a∫₀^ₐdxψ(x)e^-i^kx (7.72)

Consider a system with size L and periodic boundary conditions, ψ(x + L) = ψ(x). With such a boundary condition, we know that the wavevector for plan waves can only take discrete values

k =2πn/L (7.73) with n = … - 3, -2, -1, 0, 1, 2, 3…

代入Schrödinger eq.

-ℏ²/2m(d²∑ₖC(k)eⁱ^kx/dx²)+∑_GU(G)eⁱ^Gx∑ₖC(k)eⁱ^kx=E∑ₖC(k)eⁱ^kx

→ -ℏ²/2m∙(ik)²∑ₖC(k)eⁱ^kx+∑_GU(G)eⁱ^Gx∑ₖC(k)eⁱ^kx-E∑C(k)eⁱ^kx=0

→ (ℏ²k²/2m-E)∑ₖC(k)eⁱ^kx+∑ₖ∑_GU(G)C(k)eⁱ⁽^k+G⁾^x=0

The second term on the l.h.s. has two sums ∑ₖ∑_G . Define k = G + k and change the sum over k into the sum of k . As a result, this term becomes

∑ₖ∑_GU(G)C(k)eⁱ⁽^k+G⁾^x= ∑ₖ∑_GU(G)C(k-G)eⁱ^k^x =∑ₖ∑_GU(G)C(k-G)eⁱ^kx (7.77)

∑ₖ[(ℏ²k²/2m-E)C(k)+∑_GU(G)C(k-G)]eⁱ^kx=0 (7.78)

For plane waves, if I have a equation

∑ₖa(k)eⁱ^kx=0 (7.80)

the only solution to this equation is a(k)=0 for every k. This is because plane waves with different wave-vectors are linear independent <k|k >=0 .Therefore, if the sum over planes with different k is zero, every term in the sum must be zero. For the Schrodinger equation we

considered above, this means that

(ℏ²k²/2m-E)C(k)+∑_GU(G)C(k-G)=0 (7.81)

In our text book, it is defined λ_k = ℏ²k²/2m, so we get

(λ_k -E)C(k)+∑_GU(G)C(k-G)=0 (7.82)

This equation is known as the central equation. It is just the Schrodinger equation rewritten in the plane wave basis.

The central equation implies that C(k) is coupled with C(k+G), which includes C(k±π/a), C(k ±2 π/a), C(k ±3π/a), …

In the same time, it is easy to notice that if k - k ≠G, C(k) and C(k ) decouple from each other. C(k ) never appears in any equation of C(k) and vice versa. In other words, the value of C(k) doesn’t care about the value of C(k ).

U(x)=∑_GU(G)eⁱ^Gx=A∙a∙∑ₛδ(x-sa) i.e. delta function ∫₀^ₐδ(x-sa)dx=1 → ∫₀^ₐδ(x-a)f(x)dx=f(a)

U(G)==1/a∫₀^ₐdxU(x)e^-i^Gx=1/a∫₀^ₐdxA∙a∙∑ₛδ(x-sa)e^-i^Gx=A∑ₛ∫₀^ₐδ(x-sa)e^-i^Gxdx=A∑ₛ e^-i^G^s^a=A∑ₛ e^-i2^π^ns

G=±2πn/a reciprocal vector, 某一個U_G對應一個s值, U_G= A 代入central eq.

→ (λ_k -E)C(k)+∑ₙAC(k-2πn/a)=0 define: f(k)=∑ₙC(k-2πn/a), and f(k)=f(k-2πn/a)

→ C(k)=-Af(k)/(λ_k -E)=-[(2mA/ℏ²)f(k)]/[k²-(2mE/ℏ²)] 代入 λ_k = ℏ²k²/2m

上式用k-2πn/a代換k

C(k-2πn/a)=-[(2mA/ℏ²)f(k-2πn/a)]/[(k-2πn/a)²-(2mE/ℏ²)]=-[(2mA/ℏ²)f(k)]/[(k-2πn/a)²-(2mE/ℏ²)]

→ ∑ₙC(k-2πn/a)=-(2mA/ℏ²)f(k)∑ₙ1/[(k-2πn/a)²-(2mE/ℏ²)]

→ - ℏ²/2mA=∑ₙ[(k-2πn/a)²-(2mE/ℏ²)]⁻¹ i.e. α²=2mE/ℏ²

→ - ℏ²/2mA=∑ₙ[(k-2πn/a)²-α²]⁻¹=∑ₙ[(k-2πn/a-α)(k-2πn/a+α)]⁻¹=∑ₙ(1/2α)[(k-2πn/a-α)⁻¹-(k-2πn/a +α)⁻¹]=∑ₙ(1/2α)[a/(ka-2πn-αa)-a/(ka-2πn+αa)]

→ - ℏ²/2mA=(a/4α)∑ₙ[1/(ka/2-αa/2-πn)-1/(ka/2+αa/2-πn)] i.e. cotx=∑ₙ1/(nπ±x)

∑ₙ[1/(ka/2-αa/2-πn)-1/(ka/2+αa/2-πn)]=cot(ka/2-αa/2)-cot(ka/2+αa/2)

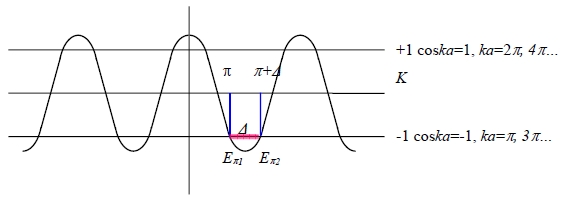
→ - ℏ²/2mA=(a/4α)[2sinαa/(cosαa -coska)]=(a/2α)[sinαa/(cosαa -coska)]

→ - ℏ²α/maA=sinαa/(cosαa -coska) → coska=cosαa+(maA/ℏ²α)sinαa=cosαa+(P/αa)sinαa

→ coska=cosαa+(P/αa)sinαa P=ma²A/ℏ²

De Broglie’s postulate:

The motion of a particle is governed by the propagation of its associated pilot waves.

Relationship between them,

pilot wave的特性:

ω=νλ=(E/h)∙(h/P)=E/P在某一瞬間, t=t₀ 可以偵測pilot wave的波形,有關粒子在空間的運動

pilot wave = a group of waves, and group velocity, g=粒子運動的速度

pilot wave function, ψ(x,t)=sin2π(x/λ-νt)=sin2π(kx-νt), k=1/λ

if ψ=0,  2π(kx-νt)=nπ n=0, 1, 2,… ⸫ xₙ=n/k+νt/k 波速, ω=dxₙ/dt=ν/k=νλ

代表粒子運動是一群pilot wave相加重疊洏成,變成一群pilot waves.

考慮兩個pilot wave相加的情況: ψ(x,t)=ψ₁(x,t)+ψ₂(x,t)

ψ₁(x,t)=sin2π(kx-νt), ψ₂(x,t)=sin2π[(k+dk)x-(ν+dν)t], i.e. sinA+sinB=2cos½(A-B)sin½(A+B)

→ ψ(x,t)=2cos2π(dkx/2-dνt/2)sin2π[(2k+dk)x/2-(2ν+dν)t/2]

≈ 2cos2π(dkx/2-dνt/2)sin2π(kx-νt) if dk<<k, dv<<v

個別pilot wave波速可以第二項求得ω=ν/k=νλ

group wave 的速度, g由第一項求得g=dv/dk=dE/dP

由相對論公式E=mc², P=mv and E²=m²c⁴+P²c²+m₀²c⁴又可證明group wave 的速度等於粒子運動的速度, g=v

g=dv/dk=dE/dP=c²P/E=c²mv/mc²=v (⸪ 2EdE=c²2PdP, dE/dP=c²P/E)

又可知ω>g ⸪ dE/dP=c²P/E → g=c²/ω≤c

Schrödinger Theorem:

總能, E_total以古典能量為定義: E=P²/2m+V若成立, 粒子速度是否等於波群速度?

ν=E/h=P²/2mh+V/h , k=1/λ=P/h → dv=2PdP/2mh, dk=dP/h ⸫ g=dv/dk=[2PdP/2mh]/(dP/h)=P/m=v

所以Schrödinger theorem:

可以滿足h/P=λ, E/h=v and E=P²/2m+V
波函數是線性組合的方程式解
位能V=V(x,t), 但特殊情況下V=V₀=constant, ⸪ F=∂V₀∕∂x=0, dP/dt=F=0 ⸫ P=const. → E=P²/2m+V=定值→ λ, v 也都是定值

Def: K=2πk, ω=2πν → P=ℏK, E=ℏω

代入E=P²/2m+V重整可得ℏω=ℏ²K²/2m+V(x,t)

因為微分方程式解為ψ(x,t)須滿足上述條件,我們可以試以ψ(x,t)=sin(Kx-ωt)是否符合ℏω=ℏ²K²/2m+V₀的形式

∂ψ∕∂x=Kcos(Kx-ωt), ∂²ψ∕∂x²=-K²sin(Kx-ωt), ∂ψ∕∂t=-ωcos(Kx-ωt)

套入微分方程式α(∂²ψ∕∂x²)+V₀ψ=β(∂ψ∕∂t)看是否符合ℏω=ℏ²K²/2m+V₀的形式

→ -αK²sin(Kx-ωt)+V₀sin(Kx-ωt)=-β ωcos(Kx-ωt)可知ψ(x,t)=sin(Kx-ωt)不合

ψ(x,t)=cos(Kx-ωt)也不合, 因此試以ψ(x,t)=cos(Kx-ωt)+γsin(Kx-ωt)

∂²ψ∕∂x²=-K²cos(Kx-ωt)-γK²sin(Kx-ωt), ∂ψ∕∂t=ωsin(Kx-ωt)-ωγcos(Kx-ωt)

代入微分方程式α(∂²ψ∕∂x²)+V₀ψ=β(∂ψ∕∂t)

→ α[-K²cos(Kx-ωt)-γK²sin(Kx-ωt)]+V₀[cos(Kx-ωt)+γsin(Kx-ωt)]=β[ωsin(Kx-ωt)-ωγcos(Kx-ωt)]

→ (-αK²+V₀+βωγ)cos(Kx-ωt)+(-αγK²+γV₀-βω)sin(Kx-ωt)=0

⸫ -αK²+V₀+βωγ=0...(a), -αγK²+γV₀-βω=0 → -αK²+V₀-βω/γ=0...(b)

(a)-(b) → βωγ+βω/γ=0, γ²+1=0 γ=±i 代入(a) -αK²+V₀=-+iβω

與ℏω=ℏ²K²/2m+V₀比較α=- ℏ²/2m, -+iβ=ℏ

因此微分方程式呈現

(-ℏ²/2m)∂²ψ∕∂x²+V₀ψ=iℏ(∂ψ∕∂t), 其解為ψ(x,t)=cos(Kx-ωt)+isin(Kx-ωt)

波動函數只有在Schrödinger theorem才存在,因其複數的特徵無法在物理世界去測量

但波動函數和粒子存在的關連,是以波的振幅強度來描述粒子存在的機率密度

born假設 at t=t₀

P(x,t)dx=ψψ*dx , ψ=R+iI and ψ*=R-iI ⸫ ψψ*= R²+I²

If ψ為(-ℏ²/2m)∂²ψ∕∂x²+V₀ψ=iℏ(∂ψ∕∂t)之解

→ ψ*就可以成為(-ℏ²/2m)∂²ψ∕∂x²+V₀ψ=iℏ(∂ψ∕∂t)…(a)的共軛方程式解

[(-ℏ²/2m)∂²ψ∕∂x²+V₀ψ=iℏ(∂ψ∕∂t)]* → [(-ℏ²/2m)∂²ψ∕∂x²]*+(V₀ψ)*=[iℏ(∂ψ∕∂t)]*

→ (-ℏ²/2m)∂²ψ*∕∂x²+V₀ψ*=iℏ(∂ψ*∕∂t)…(b)

(a)xψ*-(b)xψ → (-ℏ²/2m)[ψ*∂²ψ∕∂x²-ψ∂²ψ*∕∂x²]=iℏ[ψ*∂ψ∕∂t-ψ∂ψ*∕∂t]

化簡(-ℏ²/2m)[ψ*∂²ψ∕∂x²-ψ∂²ψ*∕∂x²]=iℏ[∂ψψ*∕∂t]兩邊積分

→ ∫(-ℏ²/2m)∂∕∂x(ψ*∂ψ∕∂x-ψ∂ψ*∕∂x)dx=∫[iℏ(∂ψψ*∕∂t)]dx

→ (iℏ/2m)(ψ*∂ψ∕∂x-ψ∂ψ*∕∂x)|_x_₁^x^₂=∂∕∂t∫_x_₁^x^₂ψψ* dx

ex.以ψ(x,t)=exp[i(Kx-ωt)]為例

ψ*(x,t)=e^-ⁱ⁽^Kx^-^ω^t⁾ → ∂ψ∕∂x=iKψ, ∂ψ*∕∂x=-iKψ*

⸫(iℏ/2m)(ψ*∂ψ∕∂x-ψ∂ψ*∕∂x)|_x_₁^x^₂=∂∕∂t∫_x_₁^x^₂ψψ*dx → (iℏ/2m)(2iKψ*ψ)|_x_₁^x^₂=∂∕∂t∫_x_₁^x^₂ψ*ψdx → ℏK/m(ψ*ψ)=∂∕∂t∫_x_₁^x^₂ψ*ψdx=v₁-v₂ ⸪ ψ*ψ=1, ℏK/m=P/m=v

對V=V₀的例子來說, v也為常數, and ψ*ψ=1對t微分,兩邊0=0

因為∫_-∞^∞ψ*ψd=1,對任何t都成立,所以(iℏ/2m)(ψ*∂ψ∕∂x-ψ∂ψ*∕∂x)|_x_₁^x^₂永遠為實數的機率通量

不含時Schrödinger equation(偏微分→常微分)

if V=V(x) → ψ(x,t)=φ(x)ϕ(t)代入微分方程式

(-ℏ²/2m)∂²φ(x)ϕ(t)∕∂x²+V₀φ(x)ϕ(t)=iℏ[∂φ(x)ϕ(t)∕∂t]

→ (-ℏ²/2m)ϕ(t)∂²φ(x)∕∂x²+V₀φ(x)ϕ(t)=iℏ[φ(x)∂ϕ(t)∕∂t]

除以φ(x)ϕ(t)

→ 1/φ(x)[(-ℏ²/2m)∂²φ(x)∕∂x²+V₀]=iℏ/φ(x)[∂ϕ(t)∕∂t] 兩邊變數不同需有共同常數解C才成立

iℏ/φ(x)[∂ϕ(t)∕∂t]=C → ∫dϕ(t)∕ϕ(t)=∫(C/iℏ)dt=-iCt/ℏ → lnϕ(t)=-iCt/ℏ, ϕ(t)=e^-^iCt^/ℏ

C/ℏ=ω, C=ℏω=E ⸫ ϕ(t)=e^-^iEt^/ℏ 波函數變成ψ(x,t)=φ(x)exp(-iEt/ℏ)

( 知識學習｜隨堂筆記 )