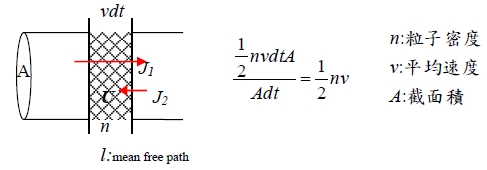字體:小 中 大
字體:小 中 大 |
|
|
|
| 2017/12/13 21:02:27瀏覽564|回應0|推薦0 | |
Chap. 5 Phonon II Thermal properties Gas Cp, Cv and Cp-Cv=R
Solid Cp-Cv=9α2βVT, α:thermal expansion coefficient of linear expansion, β:bulk modulus 能量均分原理: 每一個自由度有相等的能量(½kT) Cv=(∂U/∂T)ᵥ=3Nk (Dulong-Petit’s law), U=3NkT(動能+位能, 6個自由度) *只在高溫下適用 model 與experiment比較來證明model experiment facts about Cv of solids:
insulator: CvT3 (Debye’s T3 law) metal: CvT superconducting: Cve-A/T magnetic material: CvT3/2 Insulator絕緣體, *觀念: 能量不連續 Einstein’s model
Assume that all atoms in a solid oscillators with the same frequency. U=[∑jn]ℏω Debye’s model
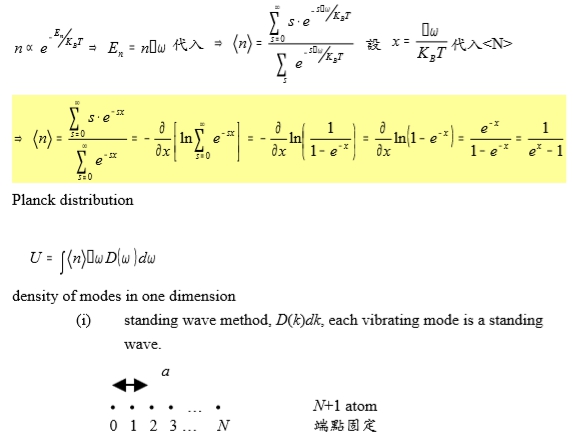
n=∑n=0∞nPₙ, Pₙ=Nₙ/∑sNₛ=e-Eₙ/kᴃT/∑s e-Eₛ/kᴃT → n=∑n=0∞ne-Eₙ/kᴃT/∑s e-Eₛ/kᴃT 代入n e-Eₙ/kᴃT → Eₙ=nℏω 代入→ n=∑ₛ=0∞se-sℏω/kᴃT/∑s e-sℏω/kᴃT , 設 x=ℏω/kᴃT → n=∑ₛ=0∞se-sx/∑s e-sx =-∂[ln∑s e-sx]∕∂x=-∂ln[1/(1-e-x)]∕∂x=∂ln(1-e-x)∕∂x=e-x/(1-e-x)=1/(ex-1) Planck distribution
→ U=∫nℏωD()d density of modes in one dimension standing wave method, D(k)dk, each vibrating mode is a standing wave.
real wave function → us(x,t)=2Asinωtsinska, us sinska and us=0=0, us=N=0sinNka=0 Nka=π, 2π , …(N-1)π, Nπ k=π/Na, 2π/Na, …(N-1)π/Na, π/a if k=π/a+π/Na, us(x,t)=2Asinωtsinska=2Asinωtsin[s(π/a+π/Na)a]=2Asinωtsin[sπ+sπ/N] =2Asinωtsin(sπ/N)(-1)s=2Asinωtsin(sπ/N) 只有N-1個atom可動 → N-1個自由度, k有N個獨立值 if k=π/a, us(x,t)=2Asinωtsinska=2Asinωtsinsπ=0測不到此波 ⸫獨立k值= π/Na, 2π/Na, …(N-1)π/Na 共N-1個k (N-1 modes) if Na=L→ k=π/L, 2π/L, …(N-1)π/L D():每單位頻率有多少值, D(k)dk=D(k)(dk/d)d=D()d One mode, π/L → D(k)=(π/L)⁻¹=L/π, 0<k<π/a
us=u₀ei(kx-ωt)=u₀ei(ska-ωt) , u(sa)=u(sa+L) → eikL=1, kL=±2nπ, k=±2nπ/L ⸫ k=0, ±2π/L, ±4π/L,..., ±Nπ/L L=Na: k與atom數目的關係 ex. N=8, L=Na, k=0, 2/8a, 4/8a, 6/8a, 8/8a(偶數只取”+”), 10/8a(/a2/8a重複) k=/a us=u₀ei[s(π/a)a-ωt]=u₀eisπe-iωt=u₀(-1)se-iωt k=-/a us=u₀ei[s(-π/a)a-ωt]=u₀e-isπe-iωt=u₀(-1)se-iωt k=0 us=u₀e-iωt ex. N=9, L=Na, k=0, 2/9a, 4/9a, 6/9a, 8/9a, 10/9a[(10/9a)= (18/9a-8/9a)= 2/a-+8/9a]
there is one mode for every 2π/L, density of mode D(k)= (2π/L)⁻¹=L/2π
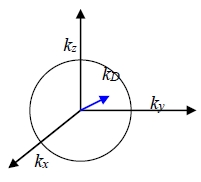
periodic boundary condition: u(r)=u(r+L)=u(r+Lx)在x方向上k=? u(r)=u(r+L)=u(r+Lx)=u₀ei(k∙r-ωt)=u₀ei(k∙r-ωt)∙eikₓ∙Lₓ → eikₓLₓ=1, kₓLₓ=±2nπ, kₓ=0, 2/Lₓ, 4/Lₓ, 6/Lₓ, …, Nₓ/Lₓ| Nₓ modes in x方向上有N個原子 同理得 eikyLy=eikzLz=1, ky=0, 2/Ly, 4/Ly, 6/Ly, …, Ny/Ly| Ny modes
kz=0, 2/Lz, 4/Lz, 6/Lz, …, Nz/Lz| Nz modes 總共有 NxNyNz個mode
Ntotal=NxNyNz, k=kₓx+kyy+kzz
考慮成正方形, D()dV每單位體積有幾個mode
U=∫nℏωD()d (2π/L)³的體積中只有含一個mode; there is one mode for every (2π/L)³ in k-space.
Density of state D(k)=(2π/L)⁻³=L³/8π³=V/8π³ D(k)dk= # of modes with wavevector between k and k+dk
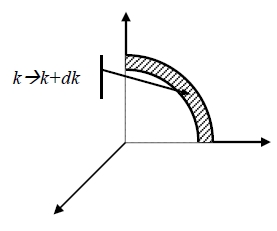
n(k)—represent the total number of modes with wave vector less than k D(k)dk=n(k+dk)-n(k) n(k)=[4πk³/3]/(2π/L)³=(V/6π²)k³ k³ D(k)dk=n(k+dk)-n(k)=([n(k+dk)-n(k)]/dk)∙ dk=(dn/dk)∙ dk → D(k)=dn/dk D(k)=dn(k)/dk=Vk²/2π² 變數轉換k→ω, D(k)dk=D(k)(dk/d)d=D()d Debye model—“sound speed” is assumed to be constant. 相速v=/k, =vk → d/dk=v group velocity D(k)dk=D(k)(dk/dω)dω=(Vk²/2π²)∙dω/v=Vω²dω/2π²v³ if there are N atoms in a crystal, there should be N phonon modes for each polarization. U=∫₀ωᴅnℏωD(ω)dω n(kᴅ)=N=n(ᴅ), [4πkᴅ³/3]/(2π/L)³=Vωᴅ³/6π²v³=N ⸫ ωᴅ=[6π²v³(N/V)]1/3 v U=∫₀ωᴅ[1/(eℏω/kᴃT-1)]ℏω(Vω²/2π²v³)dω for each polarization 1/vₗ³+1/vₜ₁³+ 1/vₜ₂³ for three polarization assume that the phonon velocity is independent of polarization,
U=3Vℏ/2π²v³∫₀ωᴅ[ω³/(eℏω/kᴃT-1)]dω=3Vℏ/2π²v³∫₀xᴅ(kᴃT/ℏ)⁴[x³/(ex-1)]dx =(kᴃ³V/6π²v³ℏ³N)9NkᴃT⁴∫₀xᴅ[x³/(ex-1)]dx=9NkᴃT(T/θ)³∫₀xᴅ[x³/(ex-1)]dx i.e. Define ℏωᴅ/kᴃ=θᴅ , Debye temperature ⸪ ωᴅ=[6π²v³(N/V)]1/3 → θ=ℏ[6π²v³(N/V)]1/3/kᴃ, ⸫ θ³=6π²v³ℏ³N/kᴃ³V Cᵥ=∂U∕∂T|ᵥ=∂{3Vℏ/2π²v³∫₀ωᴅ[ω³/(eℏω/kᴃT-1)]dω}∕∂T =3Vℏ/2π²v³∫₀ωᴅ[ω³(-ℏω/kᴃ)(1/T²)eℏω/kᴃT/(eℏω/kᴃT-1)]dω =(3Vℏ/2π²v³)(ℏ/kᴃT²)∫₀ωᴅ[ω⁴eℏω/kᴃT /(eℏω/kᴃT-1)]dω =(3Vℏ²/2π²v³kᴃT²)∫₀xᴅ(kᴃT/ℏ)⁴[x⁴ex/(ex-1)²](kᴃT/ℏ)dx =(3Vkᴃ⁴T³/2π²v³ℏ³)∫₀xᴅ[x⁴ex/(ex-1)²]dx =(Vkᴃ³/6π²v³ℏ³N)9NkᴃT³∫₀xᴅ[x⁴ex/(ex-1)²]dx=9Nkᴃ(T/θ)³∫₀xᴅ[x⁴ex/(ex-1)²]dx
U=9NkᴃT(T/θ)³∫₀xᴅ[x³/(ex-1)]dx, i.e. ex=1+x+x²/2!+x³/3!+... as |x|<<1 span=""> U=9NkᴃT(T/θ)³∫₀xᴅ[x³/(1+x+x²/2!+x³/3!+...-1)]dx≈9NkᴃT(T/θ)³∫₀xᴅx²dx = 9NkᴃT(T/θ)³(xᴅ³/3)=3NkᴃT → Cᵥ=∂U∕∂T|ᵥ=3Nkᴃ
1/(ex-1)=e-x/(1-e-x)=e-x(1+e-x+e-2x+e-3x+...)=e-x+e-2x+e-3x+...=∑ₛe-sx ∫₀∞[x³/(ex-1)]dx=∫₀∞ x³dx∑ₛe-sx=∑ₛ∫₀∞ x³e-sxdx=∑ₛ6/s⁴=π⁴/15, i.e. ζ(4)= π⁴/90
U=9NkᴃT(T/θ)³∫₀∞[x³/(ex-1)]dx=(3π⁴/5)NkᴃT(T/θ)³ → Cᵥ=∂U∕∂T|ᵥ T³ U=(3π⁴/5)NkᴃT(T/θ)³ → Cᵥ=∂U∕∂T|ᵥ=(12π⁴/5)Nkᴃ(T/θ)³=234Nkᴃ(T/θ)³ “定性”physical understanding of T3-law
kᴅ wave vector, kᴅ=ωᴅ/v=ℏωᴅ/ℏv=kᴃθ/ℏv 在低溫只有一部分k值供獻 kT=ℏωT/ℏv=(kᴃ/ℏv)T
the function of excited modes, 令密度一樣只須體積比即可 [4πkᴃ³/3]/[4πkᴅ³/3]=(kᴃ/kᴅ)³=(T/θ)³ U=3NkᴃT(T/θ)³, Cᵥ=∂U∕∂T|ᵥ=12Nkᴃ(T/θ)³ T³
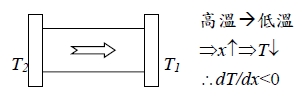
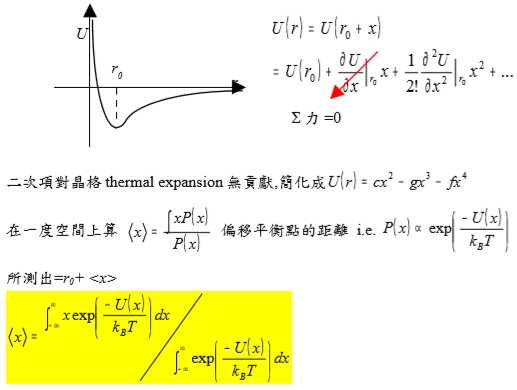
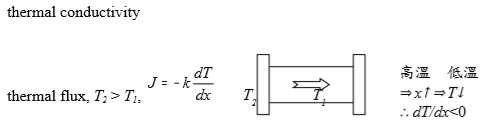
二次項對晶格thermal expansion無貢獻,簡化成U(r)=cx²-gx³-fx⁴ 在一度空間上算 x=[∫xP(x)]/P(x), 偏移平衡點的距離 i.e. P(x) exp[-U(r)/kᴃT] 所測出=r0+x x=(∫-∞∞xexp[-U(r)/kᴃT]dx)/(∫-∞∞exp[-U(r)/kᴃT]dx) upper part: ∫-∞∞xexp[-U(r)/kᴃT]dx=∫-∞∞xexp[-(cx²-gx³-fx⁴)/kᴃT]dx =∫-∞∞xexp(-cx²/kᴃT)exp[(gx³+fx⁴)/kᴃT]dx=∫-∞∞xexp(-cx²/kᴃT)(1+gx³/kᴃT+fx⁴/kᴃT)dx =∫-∞∞xexp(-cx²/kᴃT)∙(gx⁴/kᴃT)dx=(3√π/4)∙(g/c5/2)∙(kᴃT)3/2 lower part: ∫-∞∞exp[-U(r)/kᴃT]dx=∫-∞∞exp[-(cx²-gx³-fx⁴)/kᴃT]dx =∫-∞∞exp(-cx²/kᴃT)exp[(gx³+fx⁴)/kᴃT]dx=∫-∞∞exp(-cx²/kᴃT)(1+gx³/kᴃT+fx⁴/kᴃT)dx ≈∫-∞∞exp(-cx²/kᴃT)dx=(π/c)1/2∙(kᴃT)1/2 → x=[(3√π/4)∙(g/c5/2)∙(kᴃT)3/2]/[(π/c)1/2∙(kᴃT)1/2]=(3g/4c²)kᴃT thermal conductivity thermal flux, T2 > T1, J=-kdT/dx
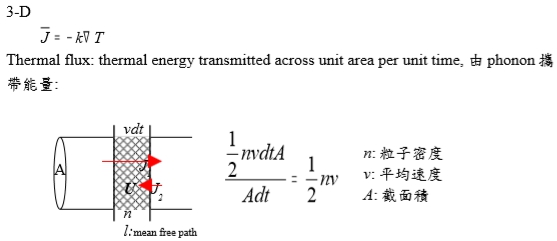
3-D, J=-kT Thermal flux: thermal energy transmitted across unit area per unit time, 由phonon攜帶能量:
Energy flux from the high temperature side: J₁=½nvₓU(T+l∙∂T/∂x)=½nvₓ[U(T)+l∙∂T/∂x(∂U/∂T)ᵥ]=½nvₓ[U(T)+cᵥ∙l∙∂T/∂x ] Energy flux from the cold temperature side: J₂=½nvₓ[U(T)-Cᵥ∙l∙∂T/∂x ] ∑J=J₁-J₂=nvₓcᵥ∙l∙∂T/∂x=Cᵥvₓ∙l∙∂T/∂x=Cᵥvₓ²τ∙∂T/∂x , l=vxτ in 3-D ∵vₓ=v²/3 → J=Cᵥv²τ∙T/3=CᵥvlT/3, k=-Cᵥvl/3 Two processes of phonon interaction
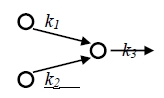
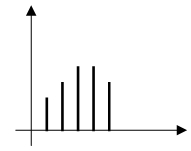
ℏk₁+ℏk₂=ℏk₃ 能量一直往前傳遞,沒有阻力
no thermal resistivity or infinite thermal conductivity.
k₁+k₂=k₃+G Finite thermal resistivity and finite thermal conductivity.
註記: □=ℏ Planck constant
|
|
| ( 知識學習|隨堂筆記 ) |



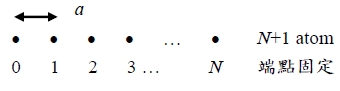
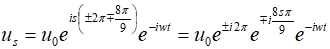
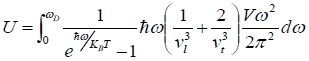 , vt
, vt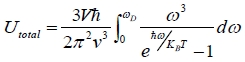 , let x=
, let x=