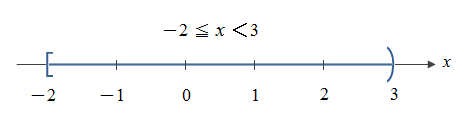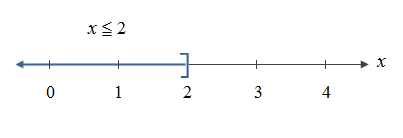
代數3

4.        【例題】解釋不等式 Interpreting Inequalities

說明以下每個不等式的實數在什麼樣的位置？在什麼數字範圍內？

a.  x≦2   b. －2≦x＜3

【解題】

a.         不等式x≦2代表所有的實數x都在2這個點或2左邊的實數線上，也就是所有的實數x都小於或等於2。實數區間用藍色線條表示。
 

b.         不等式－2≦x＜3代表實數x位於－2這個點與－2右邊的實數線上，並且在3這個實數點的左邊，不包含3這個實數點；這個「雙重不等式 double inequality」代表所有的實數x位於－2與3之間，包含－2這個實數，不包含3。實數區間用藍色線條表示。
 

5.        不等式可用來描述一組實數，不等式在數線上所指的一組實數，稱為區間intervals。以下所顯示的有限區間bounded intervals，實數a和b是每個區間的端點endpoints。

6.        封閉區間closed interval的端點包含在區間裡面，開放區間open interval的端點不涵蓋在區間之內。（注：開放open的意思不是指那組數字的實數線可以往外無限延伸，而是指代表那組數字線段，兩端沒有明確的實數數字隔離它們與外界。） 

7.        下圖是無限區間unbounded intervals。符號∞代表正無窮大positive infinity，－∞代表負無窮大negative infinity。有一些簡單的符號可以用來描述無限區間，例如（1, ∞）或（－∞,3〕。

8.        注：（1, ∞）是指從1開始往右無限延伸的實數線，但是不包含1，也就是大於1的所有正實數。（－∞,3〕是指從3開始往左無限延伸的實數線，包含端點「3」，也就是所有小於或等於3的實數。以下是無限區間的實數線： 
  

9.        【例題】使用不等式來說明區間 Using Inequalities to Represent Intervals

請利用不等式來描述以下的實數：

a.實數c，代表一組包含許許多多實數的集合，其中最大的數字是2 。

b.實數m，代表一組包含許許多多實數的集合，其中最小的數字是－3。

c. 實數x，代表一組包含許許多多實數的集合，所有的實數x在區間（－3, 5〕之內。

【解題】

a.         「實數c代表一組包含許許多多實數的集合，其中最大的數字是2」，這段描述寫成不等式： c≦2。

b.         「實數m，代表一組包含許許多多實數的集合，其中最小的數字是－3」，這段描述寫成不等式： m≧－3。

c.         「實數x，代表一組包含許許多多實數的集合，所有的實數x在區間（－3, 5〕之內」，這段描述寫成不等式： －3＜x≦5。

10.     【例題】解釋區間 Interpreting Intervals

請用文字描述以下每一個區間內的實數。

a.（－1, 0） b.〔2,∞） c.（－∞, 0）

【解題】

a.         這個區間內的所有實數大於－1、小於0，不包含－1與0。

b.         這個區間內所有的實數都大於2或等於2。

c.         這個區間內所有的實數都小於0（不包含0），涵蓋一切負實數。

n         翻譯編寫Ron Larson and David C. Falvo《Algebra and Trigonometry》