字體:小 中 大
字體:小 中 大 |
|
|
|
| 2013/07/12 08:43:12瀏覽505|回應0|推薦0 | |
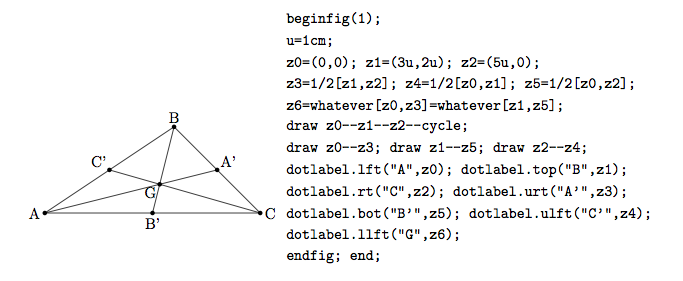
pair是坐標或向量,內含二個數值。使用方法: pair p; 宣告變數p為pair。 pair p[]; 宣告變數陣列p[]為pair,p[]為p0, p1....., P[n]的集合。n可以為任何數值0.15也行。 要給 p賦值的方法有二:一是用等式直接賦值,如: p=(9,2);%不能用p:=(9,2); 另一種就是分別把對應的x,y座標值輪入。pair的內容值分成xpart p, ypart p: xpart p=9; 或是 xpart p:=9; ypart p=2; 或是 ypart p:=9; MataPost特別定義了z為pair的宏(Marco): vardef z@#=(x@#,y@#) enddef; 這樣把z開頭的後綴(suffixes)變數名稱直接定義成為pair型態,而且其內值可以用(x,y)直接使用。 如z1=(x1,y1); z.b=(x.b, y.b);... 而xpart z1 = x1; ypart z1= y1; x1, y1可以直接用來運算。這使用上就方便很多,不需要使用 xpart z1 等運算式來算值。 另外,可以使用中括號[]來運算二個pair所形成的直線中的某一點的值: 如p1, p2為 pair變數,則p3為p1,p2的中點: p3=1/2[p1,p2]; 就是 p3=p1+1/2(p2-p1);的意思。如果z1,z2二點線段和另外z3,z4二點的線段不平行,則這二條線的交點為: z5=whatever[z1,z2]=whatever[z3,z4]; whatever表示一個任意數,這句程式的二個whatever分別是不同的值。 最簡單的例例子,就是畫三角形,並標示其重心G:
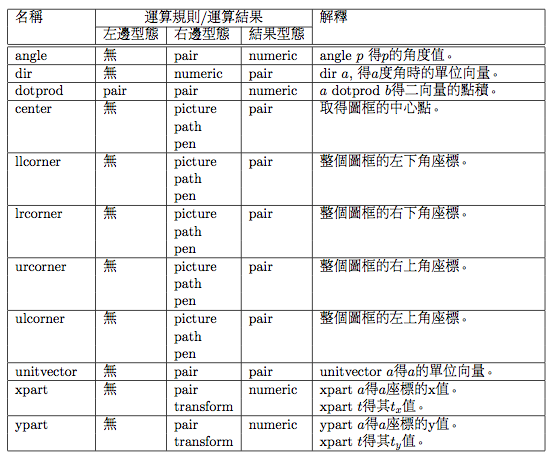
向量之間可以加減,乘除只能和數值。記得中間的單位問題,要注意使用。MetaPost提供了一些有用的運算元,對pair來作運算:
angle 用來算角度,如果是a,b,c為三個點,則a角平分線的角度,則是: 1/2*angle(b-a) +1/2*angle(c-a) dir 是算某角度的單位向量。這在做圖時很方便,如正六邊形,如 path p; for i=0 upto 5: z[i]=dir(60*i); endfor p=z0--z1--z2--z3--z4--z5--cycle; unitvector則是提供了長度1bp的單位向量。這是很重要的,因為MetaPost的數值的基本單位是bp, 而我們常的的單位可能是cm,1cm=28.34645bp。所以如果對向量也好,座標的運算也好,在相乘時如果長度單位沒注意,很容易出問題。如1cm X 1cm,結果會是28.34645cm。而1bp x 1cm 的結果才會是 1cm。unitvector這個運算元,可以把一個向量的單度單位消除成為單位向量,方便繪圖運算。 dotprod是算二向量的點積,這在算垂直的線段是很方便,用這個例子做為本章的結尾,a,b二向量,求a向量在b向量上的投影: pair a,b,c; a=(20,80); b=(60,15); c=whatever[(0,0), b]; (a-c) dotprod b=0; 這樣子,c點就會算好了,c點就是a向量在b向量上面的投影。 |
|
| ( 興趣嗜好|電腦3C ) |