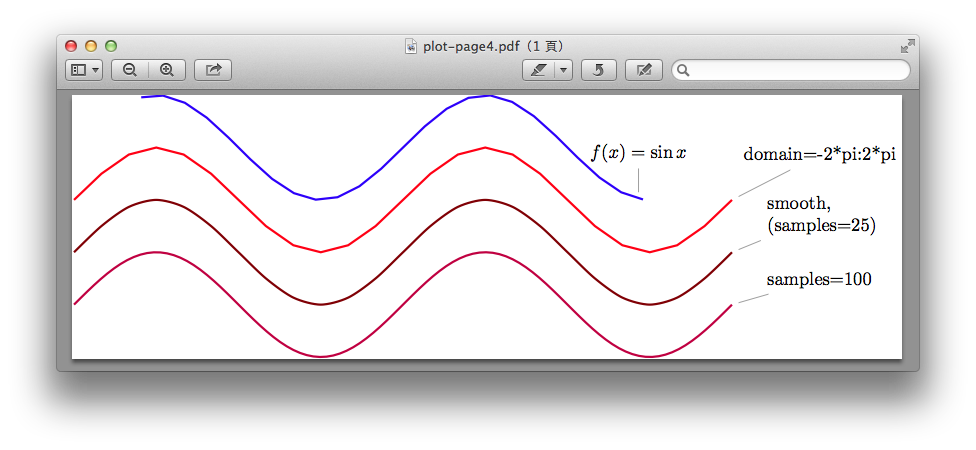
TiKz套件會自動載入pgfmath package，這裡面提供了很多函數工具。如果在latex文件中需要使用這些函數工具做運算時，則是要載入這個package：

\usepackage{pgfmath}

如果要看到運算結果，用文字方式印出來，則有\pgfmathparse使用運算指令和\pgfmathresult可以把運算結果以文字格式輸出。如在latex文件中：

\pgfmathparse{2^5}\pgfmathresult 

會印出32.0。

pgfmath 提供了哪些運算元和函數，可以看tikz文件的89節到93節的內容。或是直接看pgfmath 的套件說明。在tikz中，這些運算全部都在一組大括號中，如：

{2*sin(3 r)+cos(1.5 r)}

一些重要的定義，如

{r} 角度單位，單位是radian。sin (3) 和 sin (3 r)，二者角度值一個是3度，一個是3 radian。

{e} 數學常數

{pi}圓周率

使用plot來畫函數，有下例的控制指令：

variable=marco, 預設值是\x。

domain=start:end ，預設值是－5:5。設定變數範圍：一個數學函數，是無窮個數值的集合，而一個圖案，有版面大小的限制。所以要畫數學函數圖形，是個數值範圍的限制。有這個，才能在一個範圍內畫出圖形。

samples=numer 取樣數，預設值25

samples at =sample list，可以指定用何值取樣，可以配合foreach指令，但這命令和domain 和 samples衝突。

用正弦函數來說明plot的用法。

\draw[help lines] (-5,-4) grid (5,2);

\draw plot(\x, {sin(\x r)}); 基本上就能畫出一個正弦函數圖, 下例藍。

如果我要指定\x在-2*pi到2*pi之間，下圖紅：

\draw[red] plot[domain=-2*pi:2*pi](\x,{sin(\x r)});

實際上會讓\x在-6.28 - 6.28之間平均用含首尾在內平均25個值算過後的點，再連接起來。如果覺得直線連起來角很多，用smooth指令，連線的轉折處用圓角，能使曲線看起來更平滑。如下圓紅黑。

\draw[red!50!black] plot [domain=-2*pi:2*pi, smooth](\x,{sin(\x r)});

如果增大取樣量，那就如同微分的效果，分的越細，那麼畫出的線條就越平滑（即使都是直線相連）。預設是25, 增到100, 不用smooth，下圖紫：

\draw[draw=purple] plot [domain=-2*pi:2*pi, samples=100](\x,{sin(\x r)});

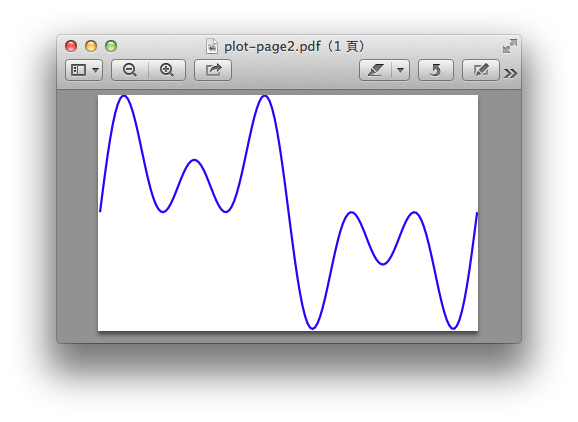
如下例，增大取樣量的效果：

\draw plot [domain=0:2*pi, smooth]({3*sin(4*\x r}, {2*sin(5*\x r)});

另外，如果基本的函數還不夠用，也可以自行設定新的函數，使用declare function命令：

declare function={ 函數命令;....;}

這是文件中的例子：

/draw [x=0.02cm,y=2cm,draw=blue, very thick] plot [domain=0:360, samples=150,

declare function={

sines(\t,\a,\b)=1+0.5*(sin(\t)+sin(\t*\a)+sin(\t*b));}](\x, {snes(\x,3,5)});

如果是\x值很大，數百，數千的函數如何表現？這個問題也不難，只要把x的單位設小一點, 如上例的x=0.02cm, y=2cm,也就是當(x,y)=(1,1)時，在圖上的位置是(0.02cm,2cm)。

declare function 也可以更複雜一些這是說明文件上面的例子，模擬聲音的函數：

\draw[help lines](0,0) grid (0,4);

\draw (0,2)-- [x=0.02cm,y=2cm, draw=red, very thick] plot [domain=0:360, samples=150, smooth, declare function={

excitation(\t,\w)=sin(\t*\w);

noice=rnd-0.5;

source(\t)=excitation(\t*20)+noise;

filter(\t)=2-abs(sin(mod(\t,90)));

speech(\t)=2+source(\t)*filter(\t);}] (\x,{speech(\x)});

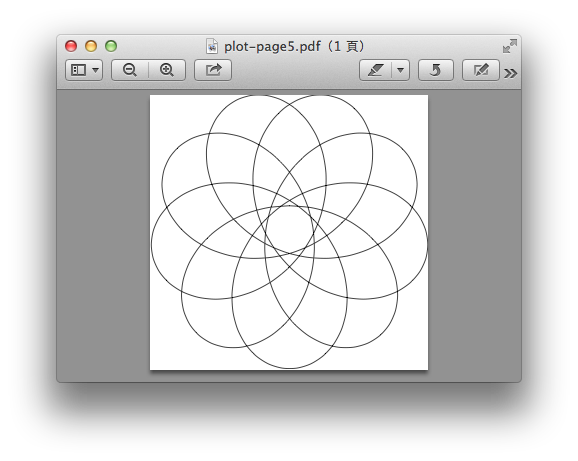
最後，是這以前我畫過的小圓挨大圓內滾動的軌跡，分別寫出(x,y)的坐標算式，然後再畫出來：

\draw plot [domain=0:720, samples=200,smooth, declare function ={

xpartt(\R,\r,\a)=(\R-\r)*sin(\a)+\r*sin((-\r/\R)*\a);

ypartt(\R,\r,\a)=(\R-\r)*cos(\a)+\r*cos((-\r/\R)*\a);}]

({xpartt(2/9, 7/9, \x)},{ypartt(2/9,7/9,\x)});

記得要注意算式，不要有分母為零的情況，例如tan(\x r)，就要注意要其值不要太接近{pi/2}。