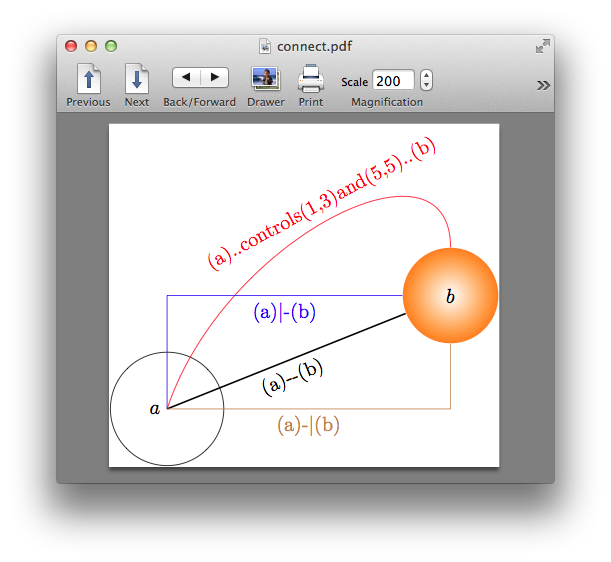
座標坐標、節點座標、節點節點的連結，基本上有三種：直線，曲線，直橫（或橫直）線。如

\coordinate [label=left:{$a$}](a) at (0,0);

\draw (a) circle (0.5);

\node[inner color=white, outer color=orange,inner sep=0.5cm] (b) at (5,2){$b$};

\draw (a)--(b);

\draw (a) controls (1,3) and (5,5)--(b);

\draw (a) -| (b);

\draw (a)|- (b);

可以看到座標和節點的不同，連到結點的邊綠時，線條就會停止。(a) -| (b)，指從a 出發，延水平線走到b的垂直投影位罝，再走垂直線到b。而 (a) |- (b)，是a 出發，往垂直方向走到b的水平投影位置，再走水平線到b。

這些連線可以加上箭頭的控制指令，變成不同的效果：

如果想要有不同的箭頭，可以使用arrows.meta library，在裡面定義了許多不同的箭頭。

線的連法也可以使用to指令：如

\cooridnate [label=left:a](a) at (0,0);

\node[draw,circle,label=right:b] (b) at (6,4);

(a)to(b)，(a)到(b)的直線；

(a)to [out=90, in=90]b，(a)到(b)的曲線，出發方向90度，進入b方向90度。

(a) to [bend right=60]b，(a)到(b)的曲線，出發方向是(a)(b)線段右方60度，進入方向是(a)(b)線段右方60度。

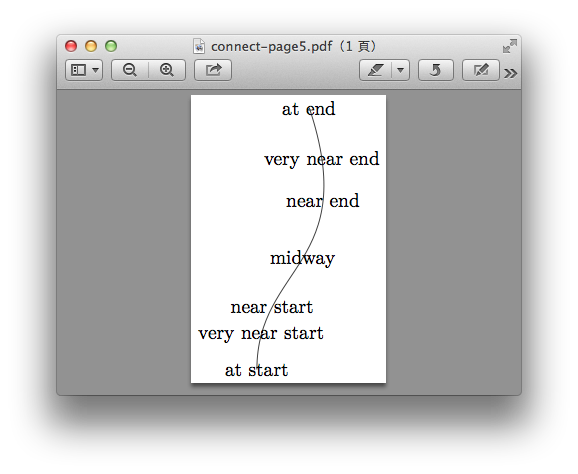
另外還有一個指令edge，用法和to很像:

\path ... edge (node or coordinate)...; 其本身的意義就是一個路徑。

用法也差不多：如果(a)(b)(c)(d)已經有了座標或結點的定義，

\path (a) edge (b)

(b) edge[->,red] (c)

(c) edge [-,dotted,black](d)

(d) edge [<-,bend left=""30,blue](a);</p">

就能畫出不同種類的連結線，這些線段也可以進行標識，主要是使用node指令（如果前面定義了every node/.style，就會受到影響，要注意）一條線段的標識，主要是位置，上下，傾斜等等參數的控制，使用直線和曲線都是一樣的。如：

\draw (0,0)--(5,3);

如這這條線要做標示，可以這樣：

\draw (0,0)--node{a}(5,3);

這樣會在線段中間的地方會有字母a畫在上面。如果想要在不同的位置，一些參數可以控制：at start, very near start, near start, midway, near end, very near end, at end，等等位位置的參數，可以控制：

\draw (0,0)-- node[near start]{b} node[midway]{a} (5,3);

另外，也可以pos參數來控制位置，pos 的參數值是0到1之間的數值，表示該線段的比例處：

\draw (0,0)-- node[pos=0.2]{a} (5,3);

\draw (2,0) to[bend left=30] (5,2);

決定了位罝後，還可以決定在該位置的哪一邊，用上(above)下(below)左(left)右(right)來控制：

-- node [pos=0.2, left] .. 在0.2位置的右方。

如果全部都在固定在某一方，如左方，可以用[auto=left]，使每個標示都在左方。

如果同一個位罝可需要不同的標示，可以用swep 或其縮寫指令"'"。在在該處（左右）一方有標示時，會自動轉換到另一邊標示。

sloped會讓文字旋轉，配合線段該處的斜率。

接下來就用實例來畫出二整數輾轉相除法求最大公因數的程式演算流程圖，這個圖定義了三程不同的node：

io: 是表示輸出輸入的node，用梯形。

op: 是表示演算過程的node，用方形。

cn: 是表示判斷過程的node，用菱形。

要使用梯形和菱形，要使用geometric library。設定好後，要使用梯型的node，就用node[io](a){};即可：

\begin{tikzpicture}[

io/.style={trapezium, trapezium left angle=70, trapezium right angle=110, fill=magenta!10, draw=magenta}

op/.style={rectangle, fill=orange!10, draw=orange},

cn/.style={diamond, aspect=2, inner sep=2pt, fill=red!10, draw=red},

node distance=5mm, thick]

\node[io] (in) {求$a,b$之最大公因數};

\node[op, below=of in] (div) {$r=a \mod b$};

\node[op, below=of div] (set) {$a=b, \ b=r$};

\node[cn, below=of set] (cond) {$b=0?$};

\node[io, below=of cond] (out) {$a$值是解答};

\path[->]

(in) edge (div)

(div) edge (set)

(set) edge (cond)

(cond) edge node[right]{Yes} (out);

\draw (cond)--node[below]{No} ++(1.5,0) |- (div);

\end{tikzpicture}