字體:小 中 大
字體:小 中 大 |
|
|
|
| 2021/08/07 05:30:13瀏覽749|回應0|推薦4 | |
§1 楔子
1990年的一個早上,衛道中學。 這時候C60(富勒稀)正夯,化學老師老蔡如是問。 我當天下午在一家寵物店買了一個很小很可愛的足球送給他,並提供他一個證明,以酬多年情誼。 §2 所謂拓撲學 把一個曲面拉長、扭曲,只要不把它戳破或兩點黏起來叫作連續變形。 連續變形後不變的性質叫作拓撲性質。 1735年,尤拉研究哥尼斯堡七橋問題預告拓撲學之門即將展開。 假設一個多面體﹐點的個數=V,邊的個數=E,面的個數=F,則V-E+F=2就是一個拓撲性質,叫作尤拉示性數,在高等幾何是一個非常重要的性質。 球面的尤拉示性數=2,其證明早期列入高中課程中,並不困難。
正多面體有五種:正四面體、正方體、正八面體、正十二面體、正二十面體。稱為柏拉圖多面體。 C60,一個有20個正6邊形,12個正5邊形所構成的多面體, 60個碳就放在60個頂點上,是一個截角正20面體,亦即將一個正20面體的每一個凸角切掉大小適當的一塊如右圖, 這樣的結構有32個面,60個頂點,以及90條邊,當然合乎60-90+32=2 §4 從理論到應用 1985年,美國萊斯(Rice)大學的克爾(Robert F. Curl 1933~)﹑斯莫利(Richard E. Smalley 1943-2005)與英國瑟息斯(Sussex)大學的克魯圖(Harold W. Kroto 1939-) 從純理論推測,有由60個碳原子所組成的空心球狀分子C60存在,三人因此共獲1996年諾貝爾化學獎。 1990年德國的克拉舒末(Wolfgang Kr tschmer 1942~)與美國的哈夫曼(Donald Ray Huffman1935~)正式宣布他們製造出C60。 1991年飯島澄男(Sumio Lijima 1939~ ﹔2002年獲頒富蘭克林物理獎)提出奈米碳管的概念後,C60將成為21世紀關鍵材料。 另一方面,製作成的奈米機器人將提供一種新的醫療方法。 至於台灣,到1992年才有台大化學系的牟中原、陸天堯等人投入。 2010年西班牙卡納利天文研究所(Instituto de Astrofisica de Canarias)的天文學家與生化學家確認在大麥哲倫星系裡的SMP48有C60。 §5 證明足球面上有12個正五邊形
§6 習作
§7 後記 C60存在於天上(大麥哲倫星系)、地上(隕石),由數學理論、實驗室到量產,由古希臘時代到現代。時空事件的轉折充滿趣味且令人深思。 魏爾(Hermann Weyl 1885~1955)在其著作" 史都華(Ian N. Stewart 1945~)1990年代寫的兩本書,"大自然的數學遊戲"與"生物世界的數學遊戲"中介紹生物數學的後續發展,說明數學是研究模式(pattern)的科學並提倡一種新的數學:形態數學(morphomatics),屬於微管的數學。 也許由研究C60引起的分子拓撲學正是大家所尋找的新數學。 我們的頭髮至少有一個漩渦,也是一個拓撲性質(覆蓋圓盤的連續切向量場一定有奇異點。),清大林文雄教授是這方面的專家。 至於為什麼我的漩渦變成地中海,那就不得而知了。 §8 參考資料
|
|
| ( 創作|另類創作 ) |



 「為什麼足球面上非有正五邊形不可?」
「為什麼足球面上非有正五邊形不可?」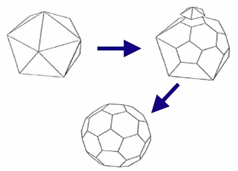 §3 C60的幾何結構
§3 C60的幾何結構