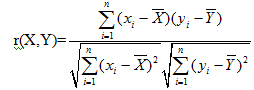一個統計學的弔詭

§ 前言

我在中學教書30多年，常常考完試，有些老師為了某些原因，要加分。

最離奇的是原始分數開根號，乘以10，再加幾分。

所以每次教學研討會幾乎都會有一個題目：如何讓命題合理化？

這個故事已有10多年了。

這一天，教學研究會，一位老師說：x老師，你出題也很難啊。

§ 突發奇想

剛好那次期末考，國三數學由我命題。我有以下如是想法。

我命了一份題目，25小題，每題4分。

我考前對每個小題給一個「預估答對率」，考完試後，作「實際答對率」，然後做兩者之間的相關係數(註1)。

我覺得這樣做，有種種好處。

1. 如果要求老師命題合理化，那麼，應該設定「預估答對率」中，對試題的難易度有所取捨。
   例如:命題老師「讓」考題中有30%的題目「預估答對率」為80%，50%的題目「預估答對率」為60%，剩下20%的題目「預估答對率」為30%，則預估的平均分數為60分。
2. 如果老師的整體預估答對率相當低，表示這位老師想開殺戒。
3. 如果老師的整體預估答對率非常高，表示這位老師想放水。
4. 最重要的是最後的試題分析。 例如，某個題目，我預估75%會做對，但實際上只有30%的人做對；或者預估30%會做對，但實際上有70%的人做對。
   這都表是老師對學生學習程度的認知值得商榷。

實務上的做法，可以設計一個電腦程式來直接算相關係數與試題分析。

事隔多年，我只記得該分考卷的預估答對率與實際答對率兩者間的相關係數為0.67，而且有3道題目,預估答對率與實際答對率有較大的偏差。

其中有一個題目是這樣的：

如右圖，一圓心角60度的扇形OAB，半徑為R，其內切圓C的半徑為r，則r/R =

我覺得這個題目相當簡單，因此預估75%的答對率，但是實際答對率只有30%，後來每次教到圓的單元，我都會測試一下，每次學生都不太會，因此可以肯定這是一道不容易的題目。身為老師的我應該有如此認知。

§ 意外的結局

我覺得以上所述的相關係數的論述與做法是非常科學的，不管是以個人或學校的立場，老師都應該適時做一下。

因此，我在後來的教學研究會提了出來。

結果是，沒有老師贊同。

會後，我問一位老師，為什麼不支持。

他說：考完就考完了嘛！

為什麼老師不支持這樣做？其實學校也蠻冷漠的,不只是第一線老師不願意做 學校行政單位也不願意施行。

§ 後記

我把上述情況告訴同學陳宏教授，他說：這對岀題老師基本上是一種出力不討好的事，搞不好是一種懲罰，所以沒有老師會「搬磚砸腳」的。

統計學的重要性是無庸置疑的，但是人為因素，社會因素想必影響了台灣統計學的發展。

陳教授在台大數學系推動統計研究所的建立，歷經20多年終於在2013年成立。

最後 我也終於明白 "美豬問題 其實是政治問題 而不是科學問題"。

註1

X表示「每小題的預估答對率」,為x1,x2,…,xn ;Y表示「每小題的實際答對率」,為y1,y2,…,yn,則X,Y的相關係數