

 字體:小 中 大
字體:小 中 大 |
|
|
|
| 2020/08/05 06:49:59瀏覽322|回應0|推薦1 | |
我知道沈昭亮教授喜歡聽江蕙的歌 所以他的"連分數"叫做"秋風夜雨話蚯蚓" 看了2018的日記 知道8/4是立秋 今年是8/7 期盼著秋風 期盼著多下幾場雨 §01 我從小學到高中 一直有學到連分數 用輾轉相除法可以求連分數 例如
真正認識到連分數是在大三上高等數論時(代數數論) 知道「連分數逼近法」是一個非常有效的逼近法。 §02 日蝕的形成原因是因為太陽、月球、地球剛好在同一條直線上,月球恰巧將太陽遮住,所以在地球上的某些區域無法看到太陽。 如果單從月相變化來看,每當月亮位於「朔」的位置,似乎就應該產生日蝕,但實際上卻並不是如此。 原因就是地球繞太陽公轉的平面(黃道面)與月球繞地球公轉的平面(白道面)有一個大約五度的夾角,必須日、月兩者的位置相距在一度內,才能產生日蝕現象;所以必須等到地球繞太陽公軌道的位置,剛好位於白道面與黃道面的兩個交點(升交點、降交點)才有可能發生日蝕的現象,亦即必須符合這兩個條件才有可能發生日蝕的現象。 如果月球位於朔的位置,且恰巧位於白道與黃道的兩個交點上,就有可能發生日蝕。 月相盈虧的平均週期約為29.530588天(稱為朔望月),而月球穿過同一黃道面的交點週期為27.212220天(稱為交點月)。 §03 連分數 交點週期=27.212220日(交點月),朔望週期=29.530588日(朔望日) 設S=n個朔望月=m個交點月,則 這個連分數的一,二,三,...次近似值(漸進分數)為 它們相差0.0361日,因此6585.3211日近似地看成朔望月與交點月的公倍數。 朔望月與交點月的最小公倍數大約為6585.32天,這個週期便是沙羅週期。 6585.32天,大約是223個朔望月,因此也常用223個朔望月來代表沙羅週期。 沙羅週期(Saros cycle)是巴比倫人發現的,經過一個沙羅週期,太陽,地球,月球回到相似的幾何位置,於是發生幾乎相同的蝕。 §04 日蝕預測 西元前6~7世紀,伊朗高原的米底亞王國(Medes,今日伊朗、阿富汗北部、土耳其東部地區 )向西征服了亞述帝國,占領它的首都尼尼微,然後繼續西進小亞細亞,遇到了米底亞王國(Lydians,今日土耳其西部 ),兩國在哈利斯(Halys今柯茲勒河)發生劇烈戰爭,連續五年未見勝負,橫屍遍野。 泰勒斯(Thales 約620BC~546BC)是希臘的數學家,哲學家,天文學家,比畢達哥拉斯年長一些,他預知5月28日下午3點(585年BC)會有日全食,於是他向交戰兩國宣布:上天對這場戰爭十分厭惡,將用日蝕向你們示警,若你們再不休戰,將有大難臨頭。 交戰雙方都不理會泰勒斯的警告,直到交戰時真的發生了日蝕,白晝變成黑夜,他們非常恐懼,於是歃血為盟,結束了戰爭。 這件事紀錄於古希臘歷史學家希羅多德(Herodotus 484BC~425BC)的著作希波戰爭史第一卷。 現代天文學的研究證明,泰勒斯時代發生在小亞細亞的唯一的一次日蝕是在公元前585年5月28日。泰勒斯到過巴比倫,他能預測日蝕,顯然他遊學巴比倫期間學得了巴比倫的天文學。 §05 後記 連分數一般的演算法是由P.A.Cataldi(1548~1626)在1613年提出,第一次有系統的研究是尤拉(L.P.Euler 1703~1783)於1737年提出。 至於國內,沈昭亮先生是我所知道的教授中,連分數的專家,參考資料中(5)(6)是他發表的連分式。
二十多年前,我當數學科召集人,請沈昭亮教授到學校演講「連分數」,沈教授千里迢迢從新竹到台中,但是 (1)學校為了"不耽誤"學生課業,就只找2,30位學生來聽 (2)學生沒有準備,因此與教授互動不足。 當時對沈教授的歉意一直在心上,至今猶不能忘懷。 沈教授曾經提到攀藤科植物的螺距...,說 這裡面有學問 最近我重讀微分幾何 於是想向沈先生請教 沒有到沈先生已於2013年過世 不勝唏噓。 在書櫃中 偶然找到一頁(兩面) 連分數 是沈昭亮上課的筆記 時隔近20多年還留著 意外(現在 把它夾在 數學史--古典篇 一書中) § 參考資料
|
|
| ( 不分類|不分類 ) |




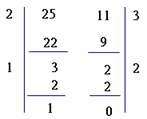 ,所以
,所以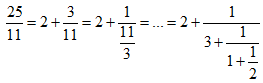 ,用[2,3,1,2]表示
,用[2,3,1,2]表示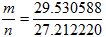 ,將它 用連分數表示=
,將它 用連分數表示=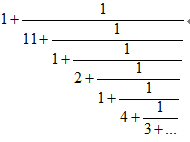
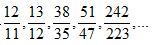 , 取到第五次近似值,即
, 取到第五次近似值,即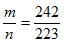 ,此時可取 m=242交點月=6585.3572日,n=223朔望月=6585.3211日。
,此時可取 m=242交點月=6585.3572日,n=223朔望月=6585.3211日。
 我在清大修碩士班學分時 認識到沈先生的風采
我在清大修碩士班學分時 認識到沈先生的風采 





